ネムネコ、熱伝導方程式を解く

ネムネコ、熱伝導方程式を解く

解く偏微分方程式は

　　

T(x,y)=X(x)Y(t)とおき、（１）に代入すると

　　

（２）式の左辺はtだけの関数、右辺はxだけの関数。

したがって、これは定数。

そこで、次のようにおく。

　　

pは定数。

なんで−p²にするかというと、そうしないと、境界条件からX(x)=0になってしまうから。

これを解くと

　　

T(0,t)=0だから、

　　

また、T(L,t)=0だから、

　　

何故ならば、A=0だと、X=0となり、解として不適だから。

よって、

　　

となるといいのだけれど、そうは問屋が許さない。

この解は、

　　

という形になる。

何故ならば、

　　

は、すべて、（１）を満たすから。

では、どうやって、係数を定めるかというと、フーリエ級数というものを使う。

フーリエ級数については、来年の夏くらいにやるとして、結果だけを述べると、t=0の境界条件、T(x,0)=x(L−x)から定まる。

　　

nが偶数のときcosnπ=1となり、nが奇数のときはcosnπ=−1になるから、nが偶数のときとなる。

ということで、

　　

少し事情があって、L=4の場合で計算すると、

　　

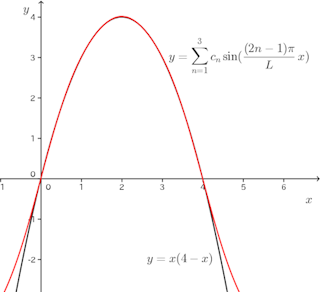
ということで、くらいで計算しても誤差はあまり大きくない。

右の図を見ると、を使って計算をすると、[0,4]でy=x(4−x)をほとんど正確に再現していることがわかる。

なんで、L=4のときを計算したかというと、昨夜、ネムネコが書いた数学の記事に関係するんだにゃ。

ネムネコが昨夜、表計算ソフトで解いた熱伝導方程式の厳密解、解析解は、上の式にκ=1/2、L=4を代入すると、

　　

アソコでの計算は、Δt=1、Δx=1という数値計算をする場合あり得ないものだったけれど、この解析解と比較すると、結構、いい値が出ている。誤差、マックス１００％くらい(^^ゞ

t=1、x=1の厳密解が約T≒2.14だから意外に正しいんだケロよ、あの計算。

tが増加するに連れて、誤差が蓄積して１００％くらい値が違うようになるけれど、意外に正しい、あの計算は。

もっとひどい結果が出ることを期待していたのだが、予想に反していたのに・・・。

１次元の非定常熱伝導方程式を表計算ソフトで解く（プチ）

１次元の非定常熱伝導方程式を表計算ソフトで解く

１次元の非定常熱伝導方程式

　　

を表計算ソフトで解けるようにしたにゃ。

ここで、ρは密度、cは比熱、λは熱伝導率、tは時刻、xは位置。

（１）は次のように変形できる。

　　

κは温度伝導率や温度拡散率などと呼ばるもので、熱ではなく、温度の伝わりやすわすさをあらわす物理量。

熱伝導率λは熱の伝わりやすさ、温度伝導率κは温度の伝わりやすさをあらわす。

熱伝導率が大きくても、密度×比熱が大きいと、温度はなかなか伝わりにくいんだにゃ。

温度Tは、時刻tと位置xの２変数関数T(x,t)になる。

粗い近似だけれど、

　　

と近似できる。

これを（２）に代入して整理すると、

　　

となる。

そして、この（３）式を元にして、（２）の偏微分方程式を解こうというわけ。

ちなみに、α=1/2のとき、

　　

という非常に簡単な計算式になる。

（４）を用いて解くことも可能。

κ=1/2とし、Δx=0.1とすると、α=1/2だから、

　　

したがって、この場合、（４）式を用いて１回計算すると、時間は0.01だけ進んだことになる。

次の問題は、この計算原理を理解するためのだケロ。

問題

　　

を、

　　

をΔx=1として、（４）式を使って解け。

【解】

（４）式を使えるのは

　　

のとき。

κ=1/2、Δx=1だから、Δt=1。

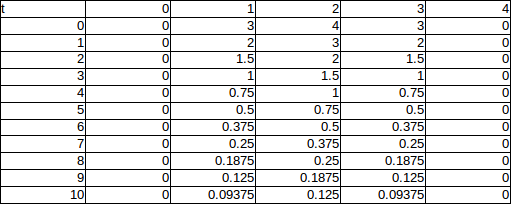
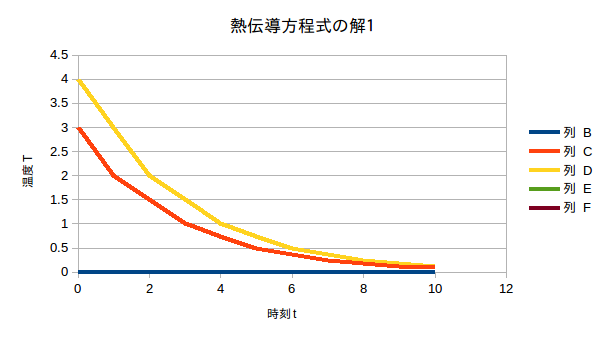
こんな計算は粗くて、この計算結果は使いものにはならないけれど、それでもこの偏微分方程式の解の特徴を比較的よくあらわしている。

最初は急激に温度が降下し、徐々に温度降下の速度が緩やかになり、両端の温度に近づいてゆく。

 

ちなみに、表計算で使った式は右の図に出ているにゃ。

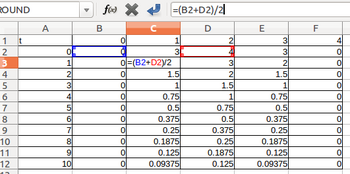
C2のセルに
=(B2+D2)/2

という計算式を書き、それをD、Eにコピペする。

B列とF列は全部０だから、予め、計算をするところにすべて０をセットしておけばいい。
こうするだけで、簡単に計算できてしまう。

C３セルの計算に使っているのは、青のB2とD2セル。

一つ前の時間の隣接するセルの値をつかって、C3セルの値を計算しているわけ。

だから、連立方程式を解かずに、次々と計算してゆくことができる。

連立方程式を使って解く方法は陰解法と呼ばれる。今回紹介したのは、陽解法の中で最もシンプルなもの。
計算の精度をあげようと思えば、Δxを小さくすればいい。
いまは、Δx=1で計算しているけれど、Δx=0.1くらいにとれば、かなり精度のいい計算ができる。
ただし、κΔt/(Δx)²=1/2の制約があるから、Δt=0.01に取らなければならず、膨大な繰り返し計算をしなければいけない。
計算量は、何と、１０００倍になる！！
だから、陽解法は、計算の原理は簡単だけれど、精度よく計算しようとすると、膨大な計算量なるので、あまり使われず、多くの場合、連立方程式を解く陰解法が使われる。

そして、ネムネコは、これよりも複雑な計算ができる表計算のスプレッドシートを公開したにゃ。
Bloggerの方にそのアドレスを記しておいたので、興味のある人は見てほしいニャ。

http://nemneko.blogspot.jp/2016/11/blog-post_81.html

エクセルで計算できるように、スプレッドシートをダウンロードできるようにもしておいたにゃ。