定積分と級数 [ネコ騙し数学]
定積分と級数
問題1
の両辺にをかけて、右辺の積を差にあらわすことにより和を求めよ。ただし、θ≠2nπとする。
の両辺にをかけると
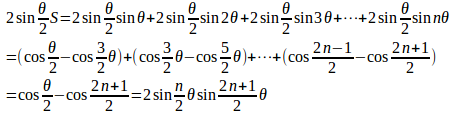
θ≠2nπだから
上の計算では、三角関数の積を和(差)にかえる次の公式を使っている。
同様に、
の両辺にをかけることによって
問題2 定積分の定義にしたがって次の定積分の値を求めよ。
閉区間[0,π]をn等分し、
区分求積法より
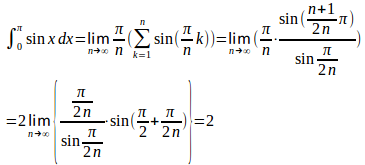
(解答終了)
問題3 nを0または正の整数とし、
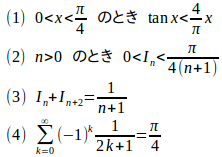
【解】
(1)
f(0)=f(π/4)=0だから、0<x<π/4のときf(x)<0。
したがって、
(2) 0<x<π/4において
(3)
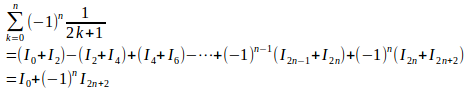
(4) n=2kとし(3)の結果を利用すると、
(2)から
タグ:微分積分
陰解法で非定常1次元熱伝導方程式を解いてみた [ネコ騙し数学]
いま、表計算ソフトで解いた熱伝導方程式を解くFortranのプログラムを作っているんだけれど、
ネムネコが予想したほど精度が出ていないケロ。
もっといい精度で計算できると思っていたんだけれど、(純)陰解法だと、時間微分が1次精度ということで、Δtを小さく取らないと、あまり良い結果が出ないね。
先に表計算ソフトで計算したものとまったく同じものを、Δx=h=0.25、Δt=0.1でt=5まで計算させてみた。
こんなものといえば、こんなものなのかもしれないけれど・・・。
計算結果は、これだにゃ。さきに表計算ソフトで計算した粗い計算結果もあわせてのせてある。exactとあるのは、この微分方程式の解析解。
表計算ソフトで計算した結果は、あの乱暴な計算にも関わらず、意外にいい結果だということがわかると思う。
少なくとも、定性的には、熱伝導方程式の特徴をよく再現していた。
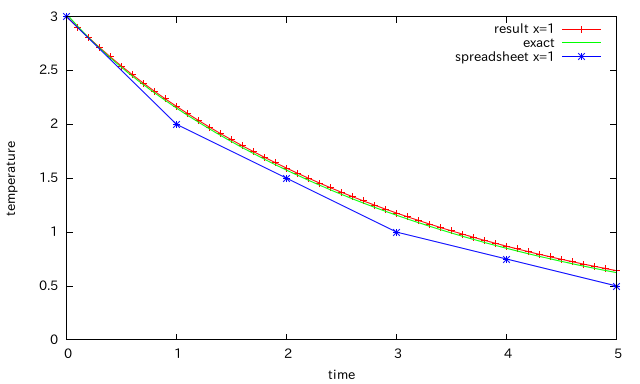
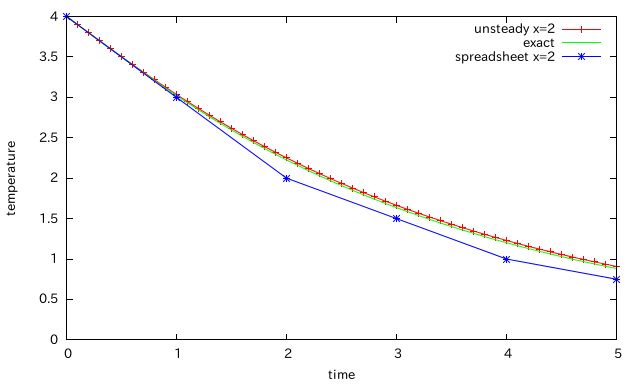
ただ、表計算で計算した陽解法の数値解はすこし振動している気配が・・・。数値解が解析解から離れかと思うと次は近づいているようですね。
1次元の非定常熱伝導方程式を表計算ソフトで解く
http://nekodamashi-math.blog.so-net.ne.jp/2016-11-20-4
上の記事で「これはα=1/2の場合」と書きましたが、α>1/2のとき、表計算で使った陽解法の解は振動する。α=1/2は陽解法の解が振動するか振動しないかの境界値。どうやら、その影響が現れているようですね。この計算はやってみて良かったにゃ。
ちょっと無駄な計算が多いプログラムと言えるのだけれど、とりあえず作ってみた程度のプログラムだからしょうないケロね。
恥ずかしいけれど、ちょっと公開してみるにゃ。
real t(0:20,0:50)
real a(20),b(20),c(20),d(20)
real k, l
t=0; a=0; b=0; c=0; d=0
n=10; m=10
l=4; k=1./2
h = l/n
time=0;
dt=0.1
! initial condition
do i=1,n-1
x=i*h
T(i,0) = x*(l-x)
end do
write(*,100) time, (t(i,0),i=0,n)
do j=1, m
do i=1, n-1
a(i)=-k/h**2
b(i)=1/dt +2.*k/h**2
c(i)=-k/h**2
d(i)=t(i,j-1)/dt
end do
d(1)=d(1)-a(1)*t(0,j); d(n-1)=d(n-1)-c(n-1)*t(n,j)
call tdma(a,b,c,d,n-1)
do i=1,n-1
t(i,j) = d(i)
end do
time=time+dt
write(*,100) time, (t(i,j),i=0,n)
end do
100 format(f7.4,1x,17(f7.4,1x))
end
subroutine tdma(a,b,c,d,n)
real a(20),b(20),c(20),d(20)
do i = 1, n-1
t= a(i+1)/b(i)
b(i+1)=b(i+1)-t*c(i)
d(i+1)=d(i+1)-t*d(i)
end do
d(n)=d(n)/b(n)
do i = n-1,1,-1
d(i)=(d(i)-c(i)*d(i+1))/b(i)
end do
end
フォートランのコンパイラを持っているヒトは、お試しあれ。
さすがに、このあたりの計算になると、入出力機能がお粗末な十進BASICでの計算は辛いね。
CやFortranでないとやっぱり辛いな。
それから、
(純)陰解法のプログラムを作ってしまうと、少しの修正で、これよりも高精度のクランク=ニコルソン法の計算プログラムを作ることができるんだケロよ。
クランク=ニコルソン法ならば、こんなにΔtを小さくしなくても精度よく計算ができる。
ネムネコが予想したほど精度が出ていないケロ。
もっといい精度で計算できると思っていたんだけれど、(純)陰解法だと、時間微分が1次精度ということで、Δtを小さく取らないと、あまり良い結果が出ないね。
先に表計算ソフトで計算したものとまったく同じものを、Δx=h=0.25、Δt=0.1でt=5まで計算させてみた。
こんなものといえば、こんなものなのかもしれないけれど・・・。
計算結果は、これだにゃ。さきに表計算ソフトで計算した粗い計算結果もあわせてのせてある。exactとあるのは、この微分方程式の解析解。
表計算ソフトで計算した結果は、あの乱暴な計算にも関わらず、意外にいい結果だということがわかると思う。
少なくとも、定性的には、熱伝導方程式の特徴をよく再現していた。


ただ、表計算で計算した陽解法の数値解はすこし振動している気配が・・・。数値解が解析解から離れかと思うと次は近づいているようですね。
1次元の非定常熱伝導方程式を表計算ソフトで解く
http://nekodamashi-math.blog.so-net.ne.jp/2016-11-20-4
上の記事で「これはα=1/2の場合」と書きましたが、α>1/2のとき、表計算で使った陽解法の解は振動する。α=1/2は陽解法の解が振動するか振動しないかの境界値。どうやら、その影響が現れているようですね。この計算はやってみて良かったにゃ。
ちょっと無駄な計算が多いプログラムと言えるのだけれど、とりあえず作ってみた程度のプログラムだからしょうないケロね。
恥ずかしいけれど、ちょっと公開してみるにゃ。
real t(0:20,0:50)
real a(20),b(20),c(20),d(20)
real k, l
t=0; a=0; b=0; c=0; d=0
n=10; m=10
l=4; k=1./2
h = l/n
time=0;
dt=0.1
! initial condition
do i=1,n-1
x=i*h
T(i,0) = x*(l-x)
end do
write(*,100) time, (t(i,0),i=0,n)
do j=1, m
do i=1, n-1
a(i)=-k/h**2
b(i)=1/dt +2.*k/h**2
c(i)=-k/h**2
d(i)=t(i,j-1)/dt
end do
d(1)=d(1)-a(1)*t(0,j); d(n-1)=d(n-1)-c(n-1)*t(n,j)
call tdma(a,b,c,d,n-1)
do i=1,n-1
t(i,j) = d(i)
end do
time=time+dt
write(*,100) time, (t(i,j),i=0,n)
end do
100 format(f7.4,1x,17(f7.4,1x))
end
subroutine tdma(a,b,c,d,n)
real a(20),b(20),c(20),d(20)
do i = 1, n-1
t= a(i+1)/b(i)
b(i+1)=b(i+1)-t*c(i)
d(i+1)=d(i+1)-t*d(i)
end do
d(n)=d(n)/b(n)
do i = n-1,1,-1
d(i)=(d(i)-c(i)*d(i+1))/b(i)
end do
end
フォートランのコンパイラを持っているヒトは、お試しあれ。
さすがに、このあたりの計算になると、入出力機能がお粗末な十進BASICでの計算は辛いね。
CやFortranでないとやっぱり辛いな。
それから、
(純)陰解法のプログラムを作ってしまうと、少しの修正で、これよりも高精度のクランク=ニコルソン法の計算プログラムを作ることができるんだケロよ。
クランク=ニコルソン法ならば、こんなにΔtを小さくしなくても精度よく計算ができる。



