関数方程式2 [ネコ騙し数学]
関数方程式2
問題1 微分可能な関数で、次の条件を満たすものを求めよ。
(1)
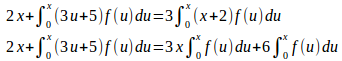
両辺をxで微分すると
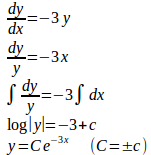
①にx=0を代入すると、
(2) x−t=uとおくと、t=x−uで、t=0にはu=x、t=xにはu=0が対応する。
また、dt=−duだから
よって、
よって、
問題2 [0,1]で定義された連続関数f(x)が連続な導関数f'(x)をもち、f(0)=2とする。
いま、この関数が、g(0)=g(1)=0をみたす[0,1]で連続な任意の関数g(x)(連続な関数g'(x)をもつとする)に対して
(1) f'(x)−3f(x)=0を証明せよ。
(2) f(x)を求めよ。【解】
(1) 部分積分すると
(2) y=f(x)とおくと
よって
タグ:微分積分



