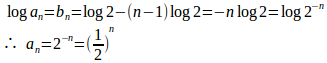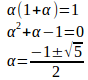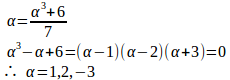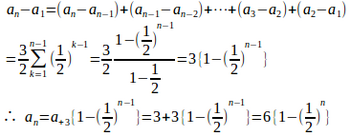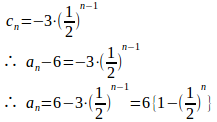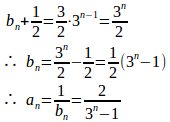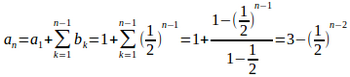確率の初歩５ 条件付き確率と事象の独立 [ネコ騙し数学]
確率の初歩５ 条件付き確率と事象の独立
§１ 条件付き確率と事象の独立
（１） 条件付き確率ある試行において、事象Aが起こったときの事象Bの起こる確率を条件付き確率といい、
であらわす。
例１ 箱の中に７個の白玉、３個の赤玉が入っており、取った玉は箱に戻さないことにする。
そして、１回目に赤玉を引く事象をA、２回目に赤玉を引く事象をBとすると、AとBの積事象A∩Bは１回目、２回目ともに赤玉を引く事象ということになる。赤玉を２度引く組み合わせの数は
通り、すべての組み合わせの数は
だから、２回とも赤玉が出る確率P(A∩B)は
したがって、１回目に赤玉が出たあとの２回目に赤玉を引く確率、条件付き確率は（１）より
これは、次のように考えることもできる。
１回目に赤玉が１個出たので、残り９個の玉の内の２個が赤玉。したがって、１回目に赤玉が出た事象に引き続いて赤玉が出る事象が起きる確率は
例２ コインを２度投げるとする。
１度目に表の出る事象をA、２度目に表の出る事象をBとすると、２度とも表の出る事象はA∩B。 
問題１ ボルト工場において、機械A、Bは全体の６０％、４０％を作り、その製品のうちそれぞれ２％、５％が不良品であるとする。
製品の中から任意の一本のボルトが選ばれるとする。（１） そのボルトが不良品である確率を求めよ。
（２） その不良品が機械Aで作られた確率を求めよ。【解】
（１） 機械A、Bで製品が作られた事象をA、B、不良品である事象をCとすると、 
（２）
解いただけです。
問題１の解を読んで何をやっているかわからなくても、悲観しないでください。これはそういう問題ですから。
（２） 事象の独立
２つの事象A、Bがあって、一方の事象が他方の確率に影響を与えないとき、すなわち、 
§２ 乗法定理
（１） 任意の事象A、Bについて 
問 さいころを１回振る。事象Aと事象Bは独立か従属かを答えよ。
（１） A：２の倍数が出る B:３以上の目が出る（２） A:３の倍数が出る B：３以上の目が出る
【解】
（１）
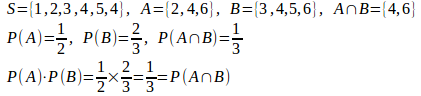
よって、独立である。
（２）
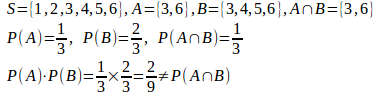
よって、独立でなく、従属である。
（解答終了）
§３ 独立試行の確率
１回の試行で事象Aの起こる確率がpであるとすると、この試行をn回独立に繰り返した場合、事象Aがr回起こる確率は
例 コインを５回投げるとする。このとき、表の出る確率pはp=1/2。
したがって、表が３回出る確率
は
問 １枚の硬貨を何回も投げてゆき、表の出た回数が２になったところでやめにする。ちょうど１０回投げたところで止めになる確率を求めよ。
【解】ちょうど１０回で止めになるのは、９回までに表が１回出て、ちょうど１０回目に２回目の表が出る場合。
表の出る確率は1/2で、表が１回、裏が８回出る確率は 
確率の初歩４ 確率の定義 [ネコ騙し数学]
確率の初歩４ 確率の定義
§１ 確率の定義と用語の定義
標本空間 ある試行で起こりうる結果の全体集合
Sを標本空間、e₁、e₂、・・・を標本空間の要素とすると 
事象 標本空間Uの部分集合。
A、BをSの部分集合とするとき、A∪Bを和事象、A∩Bを積事象、
をAの余事象という。A∩B=∅のとき、AとBは排反である、または、排反事象であるという。
確率の定義
事象Aの要素の個数をn(A)、標本空間Sの要素の個数をNとするとき、事象Aの起こる確率P(A)は 
例１ さいころを１回振る試行を考える。このとき、標本空間Sは
偶数の目が出る確率、つまり、事象Aの確率は、
§２ 確率の基本的性質
（１） 任意の事象Aについて
（２） 標本空間Sの起こる確率は
（３） 空事象∅の起こる確率は
（４） 事象Aと事象Bが排反、つまり、A∩B=∅であるとき、AとBの和事象A∪Bの起きる確率は
A∩B≠∅のときは
（５） 事象Aの余事象の起きる確率は
例２ さいころを１回振るとする。偶数の目が出る事象をA、奇数の目が出る事象をB、2以下の目が出る事象をCとすると、
①と②の結果は一致する。
また、AとCの和集合A∪Cは
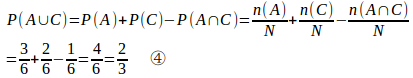
となり、③と④は一致する。
A∩B=∅だから
さらに、
だから、BはAの余事象である。
問１ １組５２枚のトランプから４枚抜くとき、次の確率を求めよ。
（１） ２枚はクラブ、２枚はハートが出る確率（２） ４枚とも同種類のカードが出る確率
（３） ４枚とも異なる種類のカードが出る確率【解】
（１） 
（２）
（３）
問２ １から５０までの番号をつけた５０枚の札から１枚取り出したとき、その番号が２または３の倍数である確率を求めよ。
【解】５０以下の生成数の、２の倍数の集合をA、３の倍数の集合をBとすると、n(A)=25、n(B)=16。
また、「２の倍数」かつ「３の倍数」の集合は、６の倍数の集合なので、n(A∩B)=8。よって、
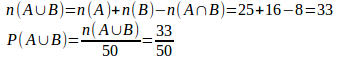
（解答終了）
確率の初歩３ 組み合わせ [ネコ騙し数学]
確率の初歩３ 組み合わせ
組み合わせに入る前に、同種のものを含む順列。
§１ 同種のものを含む順列
n個のうち、p個は同じもの、q個は同じもの、r個は同じもの、・・・・・・であるときの順列の数は
例 赤い玉が５個、青い玉が３個、黄色の玉が２個で計１０個の玉の順列の数は
問 ８枚のカード、A、A、B、B、C、D、E、Fのすべてを１列に並べる。
（２） 同じカードが隣り合わない並べ方は何通りか。
【解】（１） ８枚のカードのうち、Aと同種のカードが２枚、Bと同種のカードが２枚あるので
AA、BBの一方だけが隣り合う並び方は
したがって、
（註）
AAとAが連続してならんでいる並べ方は、AAを１枚のカードと考えて、カードを７枚並べる順列の数と等しい。つまり、７！通り。
この７！通りの中にはBBと、Bが２枚連続してならんでいる並び方が６！通りあるので、AAとAだけが２万連続でならんでいる並び方は７！−６！通り。BBとBが２枚連続して並ぶ場合も同様で、AA、BBの一方だけの順列の数は
§２ 組み合わせ
異なるn個からr個（r≦n）とった組み合わせの数は
問１ 男子１０人、女子５人のうちから、５人の候補を選ぶとき
（１） 全部で何通りの方法があるか。（２） 男子の委員を３人、女子の委員を２人とすれば何通りになるか。
（３） 特定の２人、甲、乙が必ず選ばれる方法は何通りか。【解】
（１） 男女１５人から５人選ぶのだから 
（２） 男子１０人から３人選ぶ組み合わせは
通り、女子５人から２人選ぶ組み合わせは
通り。
（３） 甲乙の２人は必ず選ばれるので、残りの１３人から３人を選ぶことになる。
よって 
問２ ６人がある旅館に泊まるのに、２ずつ３室に分かれることになった。
（１） ６人を２人ずつ、A、B、Cの３室に入れる方法は何通りあるか。（２） ６人を２人ずつ、単に３室に分ける方法は何通りか。
【解】（１） A室には６人のうち２人を、B室には４人のうちの２人、C室には残りの２人を入れる。
したがって、 
（２） この場合、A、B、C室という部屋の区別がないので（１）で求めた９０通りを３！=6で割らないといけない。
よって、 
問２の（１）、（２）の違いがわかりますか？
そして、次の問題で混乱の極みに突き落とす(^^ゞ
問３ 男子１０人、女子６人の庭球選手の中から混合ダブルスのチームを作るとすると、作り方は何通りあるか。
【解】 
この３！は何処から出てきたのだろうか(^^)
は、妖怪１０人から｛アリス、正邪、ぬえ｝を選び、人間６人の中から｛霊夢、魔理沙、咲夜｝の３人、合せて６人を選ぶ場合の数。
確率の初歩２ 順列 [ネコ騙し数学]
確率の初歩２ 順列
順列 異なるn個の中からr個（r≦n）とった順列
は
ここで、
例 ５人を一列に並べる並べ方（順列）は
問１ 次の等式を証明せよ。
問２ 男子１０人、女子５人の生徒の中から会長、副会長、書記を選ぶとする。次の問いに答えよ。
（１） 全部で何通りの選び方があるか。（２） その中に少なくとも１人の男子を選びたい。このような選び方は何通りあるか。
【解】（１） 男子１０人、女子５人、あわせて１５人の中から会長、副会長、書記の３人を選ぶのだから
（２） 男子が１人も含まれない、つまり、すべて女子の場合の数は、女子５人から３人を選ぶので
（解答終了）
問３ 0,1,2,3,4,5の６つの数字からなる異なる４つの数字を選び出し、４桁の数字を作るとき、次のものは何通りあるか。
（１） 全部（２） 偶数
【解】（１） ４桁の数字をabcdとすると、aに選べる数字は１〜5の5通り。
bcdに関しては、aに選んだ残りの5つの数字から３つ選べばよい。よって、
（２） abcdが偶数になるのは、dが0,2,4のとき。
d=0のとき、残りの５つから３つ選んで並べれば良いので
したがって、
したがって、60+48+48=156の１５６通り。
（解答終了）問４ 男子４人、女子３人を並べるとする。
（１） 全部で何通りの並べ方があるか。（２） 女子３人は必ず隣り合うものとすると、全部で何通りの並べ方があるか。
（３） 女子はどの２人とも隣り合うように並べると何通りの並べ方があるか。【解】
（１） ７！=7×6×5×4×3×2×1=5040通り（２） 隣り合う３人の女子を１人と考え、５人を並べる並べ方は
（３） これは次のように考えるといいにゃ。
女子は△の５つのところに３人並べればよいので、その並べ方は
（解答終了）
問５ 異なる３個の箱を異なる４個の箱に分配するとき、
（２） どの箱にも２個以上のボールを入れない場合、全部で何通りの分配する方法があるか。
【解】（１） 4³=64通り
（２） 
通り
（１）については、３個のボールをA,B,Cとすると、ボールA,B,Cともにそれぞれ４通りの分配の仕方があるので、
これを箱から考えると、
左辺第１項は１個ずつ分配する仕方、第２項は２個と１個、第３項はボール３個を分配する仕方である。
だから、を
としてもよい。
ボール２個を先に箱に入れて、残った３個の箱に２個の玉を一緒に入れるか、２個の玉を先に入れて、残った３個の箱に１個入れるかという考え方の違いに過ぎないので、式の形にこだわる必要はない。
（１）のように重複を許す順列を重複順列という。
この他に、n個の異なる珠を数珠つなぎにn個並べる円順列などがありますが、円順列の場合の数は
通りです。確率の初歩１ 場合の数 [ネコ騙し数学]
確率の初歩１ 場合の数
高校程度の統計をやる前に、これから数回にわたって、その前提知識として必要になる、場合の数と確率について少しだけ述べることにする。
§１ 和の法則
和の法則
２つの事柄A、Bがあって、同時に起こらないとする。Aの起こり方がm通り、Bの起こり方がn通りであるとすれば、AまたはBの起こる場合の数、m+n通りである。
同時に起こらないということは、右図（ベン図）で示される集合Aと集合Bが交わりA∩Bをもたない、つまり、A∩Bが空集合∅、つまり、
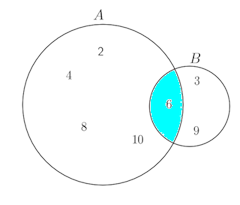右図に示されるように、AとBの交わりが空集合でないとき、集合A、Bの集合の元（要素）の個数をn(A)、n(B)などとあらわすことにすると、集合Aと集合Bの和集合A∪Bの元の個数n(A∪B)は
例 
とすると、
（１）式は、A、Bが無限集合の場合、必ずしも成り立たないので注意が必要。
問１ １から１０００までの正の整数のうち、５または７の倍数の個数はいくつあるか。
【解】１から１０００までの正の数のうち、５の倍数である集合をA、７の倍数である集合をBとする。
そうすると、A∩Bは、１から１０００までの整数のうち、「５の倍数であり、かつ、７の倍数」、つまり、「３５の倍数」の集合。n(A)=200、n(B)=142、n(A∩B)=28だから、
（解答終了）
問２ １００人の生徒の中で、音楽の愛好者は５３人、スポーツの愛好者が７２人いる。音楽とスポーツの両方を愛好する生徒数をn人とすると、nの取りうる最小値と最大値を求めよ。
【解】音楽の愛好者の集合をA、スポーツの愛好者の集合をBとすると、n(A)=53、n(B)=72、n(A∩B)=n。
で、A∩B⊆Aだから、 
したがって、nの最小値は25、最大値は53。
（解答終了）
問３ ２桁の正の整数のうち、一位の数字が十位の数字よりも小さいものはいくつかるか。
【解】十位の数字が１のとき、一位の数字は0で１個。
十位の数字が２のときは、一位の数字は0と1の２個。十位の数字がn（=1〜9）のとき、１位の数字は0,1,・・・,n−1のn個。
したがって、 
（解答終了）
§２ 積の法則
積の法則
２つのことがらA、Bがあって、Aの起こり方がm通り、Aのおのおのの起こり方に対して、Bの起こり方がnとおりであれば、Aに引き続いてBの起こる場合の数はm・n通りである。問１ N=9800の正の約数は、１とNを含めていくつあるか。
【解】N=9800を素因数分解すると、
（解答終了）
問２ 0,1,2,3,4,5の６個の数字がある。個の中から３個の活字を並べてできる３桁の整数のうち４３２以下の整数はいくつできるか。
【解】百位が４のとき、十位が３ならば、一位は0,1,2の３通り。
百位が４のとき、十位が0,1,2ならば、一位はそれぞれにつき4通りあるので、3×4=１２通り。百位が１〜３のとき、十位は５通り、一位は４通り。したがって、３×５×４＝６０通り。
よって、３＋１２＋６０＝７５通り。（解答終了）
第１４回 漸化式で表された数列の極限 連立漸化式 [ネコ騙し数学]
第１４回 漸化式で表された数列の極限 連立漸化式
問題１ 数列
はx₁=1、y₁=5をもとにして
にしたがって作られている。このとき、
および
を求めよ。
①から
ここで,t²−4t+3=0として、この２次方程式を解くと、
⑥より
は初項x₂−x₁、公比3の等比数列。
⑦より、数列
は一定だから――初項x₂−3x₁、公比1の数列と考えてもよい――
⑩−⑪
上のように隣接３項の漸化式に変形して解くことができるけれど、実はうまい方法がある。
【別解】
①+②
③より、数列
は、初項x₁+y₁、公比3の等比数列だから
⑤−⑥
【別解終了】
どちらが楽かは言うまでもないだろう。
この他に、
問題２
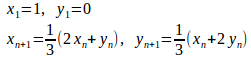
に対して次の問いに答えよ。
（１） 
をnの式であらわせ。
（２） 
を求めよ。
（１）
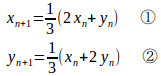
①＋②
④より数列
は初項x₁−y₁=1、公比1/3の等比数列。
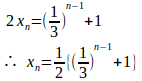
⑤−⑥
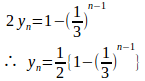
（２）
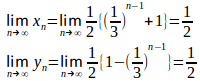
（解答終了）
問題３ 
が次の条件を満たすとき、
を求めよ。
【解】
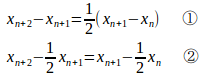
①より、
②より
④−③
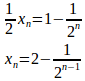
で、
よって、
【別解】
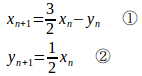
①−②
①−２×②
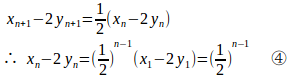
③、④より
第１３回 漸化式で表された数列の極限４ 隣接する３項の場合 [ネコ騙し数学]
第１３回 漸化式で表された数列の極限４ 隣接する３項の場合
隣接する３項の漸化式の一般形は
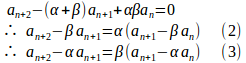
と変形できる。
（２）は数列
が初項a₂−βa₁、公比αの等比数列であることを表すので、
（３）は数列
が初項a₂−αa₁、公比βの等比数列であることを表すので、
α≠βならば、（６）をα−βで割ることによって、一般項
を得ることができる。
両辺を
で割ると
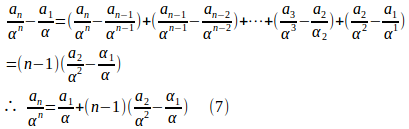
では、問題を。
問題１ 次のように定められた数列
について
を求めよ。
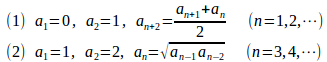
【解】
（１）
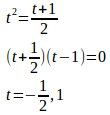
よって、
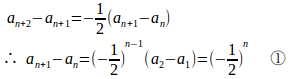
また
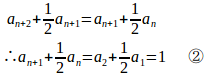
②−①は
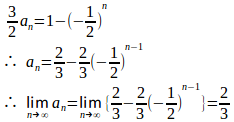
（２）
とおくと、①は
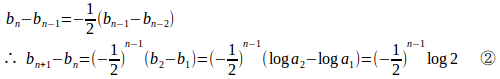
また、
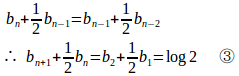
③−②
（解答終了）
問題２
で定義される数列について次の問いに答えよ。
（１） はどんな数列か。
（２） n項までの和
を求め、
を求めよ。
【解】
（１） 
とおくと
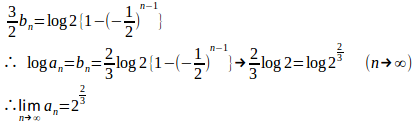
よって、
は初項b₁=log2、公差−log2とする等差数列。
（２）
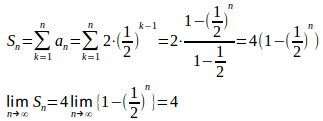
（解答終了）
問題３
（１） 数列、1,2,3,5,8,13,21,34,・・・はどんな規則でできているか。その規則を式であらわせ。
（２） 上の数列の第n項を第n+1項で割ったものをとおくとき、
を求めよ。【解】
（１） 
（２）
両辺を
で割ると、
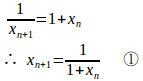
で、
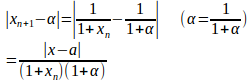
だから
で、
ちなみに、問題３に出てくる数列をフィボナッチ数列という。
第１２回 漸化式で表された数列の極限３ 隣接する２項の場合２ [ネコ騙し数学]
第１２回 漸化式で表された数列の極限３ 隣接する２項の場合２
問題１ 
を満たす数列
がある。
（１） 
とおくとき、と
との関係式を求めよ。
（２） 0<x₁<1のとき、
を求めよ。
【解】
（１）
だから、
（２） 0<x₁<1より、0<y₁<1、また
。
したがって、数列
は初項logy₁、公比2の等比数列。
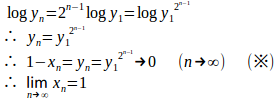
（解答終了）
（※） 
とおくと、
問題２ aは1<a<2を満たす定数とする。
によって定められた数列
について、次の問いに答えよ。
（１） 
を証明せよ。
（２） 
を証明せよ。
（３） 
を求めよ。
（１） n=1のとき
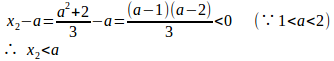
よって、
n=k+1のとき
だから、
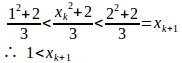
また、
よって、数学的帰納法により、
（２） 
（３）
ここで、
問題３ 次の数列について、下の問（１），（２）に答えよ。
（２） この数列が収束することはわかっていて、その極限値を求めよ。
【解】（１） n=1のとき
n=kのとき、
（２）
また、
よって、極限値α=1
（解答終了）
第１１回 漸化式で与えられた数列の極限２ 隣接する２項の場合 [ネコ騙し数学]
第１１回 漸化式で与えられた数列の極限２ 隣接する２項の場合
前回にひき続いて、今回も漸化式で表された数列の極限の問題を解くことによって、その解法を紹介することにする。
今回は、漸化式の最も基本的な隣接する２項の場合。問題１ 次のように定められた数列の極限値を求めよ。
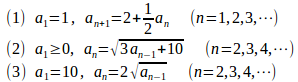
【解】
（１） 
したがって、数列
は初項
、公比1/2とする等比数列。
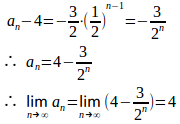
（２）
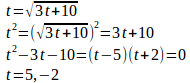
で、
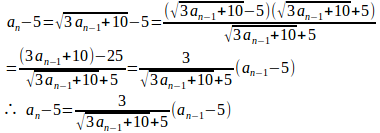
ここで、両辺の絶対値をとる。
だから
（３）
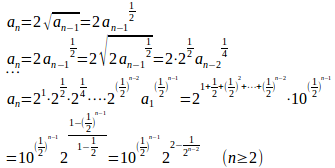
よって、
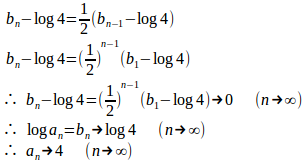
（解答終了）
（２）、（３）から分かるように、漸化式で与えられた数列の極限を求める場合、必ずしも一般項を求める必要はない。
問題２ 一般項が次のように与えられる数列の一般項を求め、
と求めよ。
とおくと、
したがって、数列
は初項−1、公差−1の等差数列。
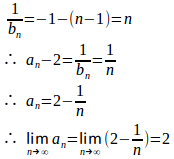
（解答終了）
なのですが、
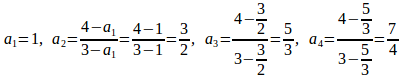
と順次計算し、これから
――分子は2ずつ増え、分母は1ずつ増えているのだから、上のように推測できる――
それから、
数学的帰納法を使って
第１０回 漸化式で表された数列の極限１ [ネコ騙し数学]
第１０回 漸化式で表された数列の極限１
具体的に問題を解くことによって、漸化式で表された数列の極限を求める基本的な解法を学ぶことにする。
その前に、総和記号Σの定義 
公比r、初項aとする等比数列の一般項は
また、漸化式で等比数列を表すと
問題１
について、次の問いに答えよ。（１） 階差
を調べてを求めよ。
（２） 
とおいて定められる数列
を調べて、を定めよ。
（３） を求めよ。
【解】
（１） 
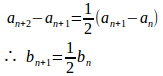
したがって、数列は初項
、公比1/2の等比数列。
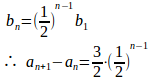
よって、
（２）
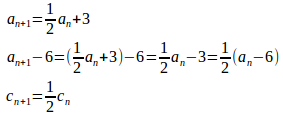
したがって、数列
は、初項c₁=a₁−6=−3、公比1/2の等比数列。
（３）
（１）では、
のとき
問題２ 数列がある。
（１） 
とおいて定められる数列を調べてを定めよ。
（２） を求めよ。
（１）
したがって、数列
は初項
、公比3の等比数列。
（２）
問題３ 数列
の項の間に次の関係がある。
（１） 
とおいて
に関する漸化式を求めよ。
をnの式であらわせ。（３） を求めよ。
（１）
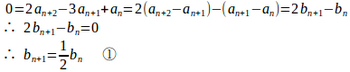
（２） ①より、数列は初項b₁=a₂−a₁=1、公比1/2の等比数列。
（３）
ゆえに、
