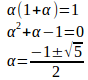第１３回 漸化式で表された数列の極限４ 隣接する３項の場合

第１３回　漸化式で表された数列の極限４　隣接する３項の場合

隣接する３項の漸化式の一般形は

　　

２次方程式t²+pt+q=0の実数解をα、βとすると、２次方程式の解と係数の関係から

　　

となるので、（１）は
　　

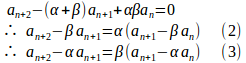
と変形できる。

（２）は数列が初項a₂−βa₁、公比αの等比数列であることを表すので、

　　

（３）は数列が初項a₂−αa₁、公比βの等比数列であることを表すので、

　　

（４）−（５）は

　　

α≠βならば、（６）をα−βで割ることによって、一般項を得ることができる。

α=βのとき、

　　

両辺をで割ると

　　

よって、

　　

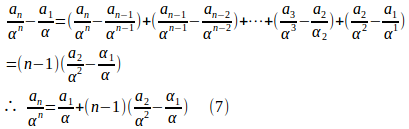
では、問題を。

問題１　次のように定められた数列についてを求めよ。

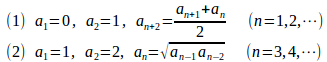
【解】

（１）
　　

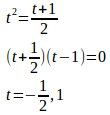
よって、

　　

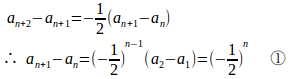
また

　　

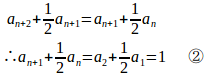
②−①は

　　

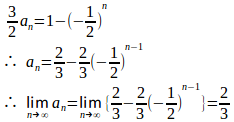
（２）

　　

の両辺の対数をとると、
　　

とおくと、①は

　　

よって、
　　

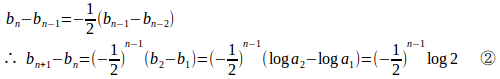
また、

　　

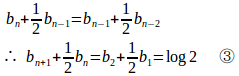
③−②

（解答終了）

問題２

　　

で定義される数列について次の問いに答えよ。

（１）　はどんな数列か。

（２）　n項までの和を求め、を求めよ。

【解】

（１）

　　

の両辺の対数をとると、

　　

とおくと
　　

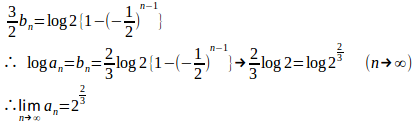
よって、は初項b₁=log2、公差−log2とする等差数列。

したがって、

　　

（２）

　　

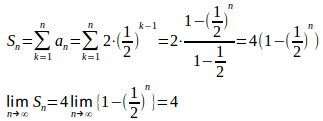
（解答終了）

問題３

（１）　数列、1,2,3,5,8,13,21,34,・・・はどんな規則でできているか。その規則を式であらわせ。

（２）　上の数列の第n項を第n+1項で割ったものをとおくとき、を求めよ。

【解】

（１）

　　

（２）

　　

両辺をで割ると、

　　

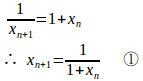
よって、
　　

で、

　　

とおき、これを解くと

　　

となるので、あらためて

　　

とおいて、①の両辺をαで引くと
　　

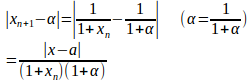
だから

　　

で、

　　

よって、

　　

したがって、

　　

よって、

　　

（解答終了）

ちなみに、問題３に出てくる数列をフィボナッチ数列という。

タグ：極限 数列