第14回 漸化式で表された数列の極限 連立漸化式 [ネコ騙し数学]
第14回 漸化式で表された数列の極限 連立漸化式
問題1 数列はx₁=1、y₁=5をもとにして
にしたがって作られている。このとき、および
を求めよ。
①から
ここで,t²−4t+3=0として、この2次方程式を解くと、
⑥よりは初項x₂−x₁、公比3の等比数列。
⑦より、数列は一定だから――初項x₂−3x₁、公比1の数列と考えてもよい――
⑩−⑪
上のように隣接3項の漸化式に変形して解くことができるけれど、実はうまい方法がある。
【別解】
①+②
③より、数列は、初項x₁+y₁、公比3の等比数列だから
⑤−⑥
【別解終了】
どちらが楽かは言うまでもないだろう。
この他に、
問題2
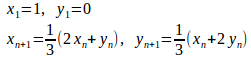
に対して次の問いに答えよ。
(1) をnの式であらわせ。
(2) を求めよ。
(1)
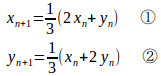
①+②
④より数列は初項x₁−y₁=1、公比1/3の等比数列。
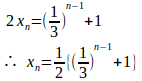
⑤−⑥
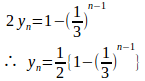
(2)
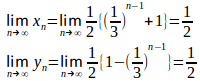
(解答終了)
問題3 が次の条件を満たすとき、
を求めよ。
【解】
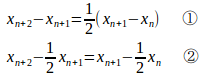
①より、
②より
④−③
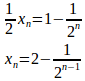
で、
よって、
【別解】
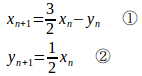
①−②
①−2×②
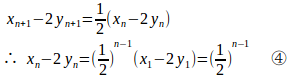
③、④より



