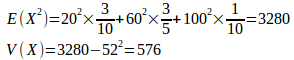第１８回 統計のまとめ

第１８回　統計のまとめ

§１　確率変数と確率分布

（１）　確率変数と確率分布

変量Xのとる値、およびXのこれらの値が取りうる確率が定まっているとき、変量Xを確率変数といい、との対応関係を確率分布という。

（２）　確率変数の平均と標準偏差

①　平均（値）・期待値
　　

②　標準偏差σ

　　

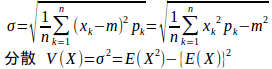
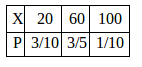
問題１　つぼの中に５個の球がはいっている。そのうち、３球には１０点、他の２個の球には５０点の印がついてある。ツボの中から２個の球を同時に取り出す。その２個の球の和を表す確率変数をXとする。このとき

（１）　Xの確率分布を求めよ。

（２）　Xの平均（期待値）、および、分散を求めよ。

【解】

（１）　X=20の確率は

　　

X=60の確率は

　　

X=100の確率は
　　

（２）　平均値mは

　　

分散σ²は

　　

（解答終了）

分散を求めるために、

　　

を使うのならば、

　　

§２　二項分布

２項分布
　　

においては

　　

問題２　３枚の硬貨を投げる試行を５００回繰り返すとき、２枚が表、１枚が裏の出る回数をXとする。Xの確率分布の平均と標準偏差を求めよ。

３枚の硬貨を投げたとき、２枚が表、１枚が裏である確率pは
　　

したがって、

　　

２枚が表、１枚が裏の出る回数Xは二項分布に従うので、平均値mと標準偏差σは

　　

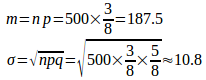
（解答終了）

§３　チェビシェフの定理

平均値m、標準偏差σの分布では
　　

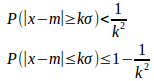
§４　確率密度関数と正規分布

（１）　確率密度関数

変量Xの変域をa≦X≦b、確率密度関数をf(x)とすると

　　

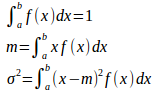
問題３　変量Xの変域が0≦X≦1で、確率密度関数が

のとき、

（１）　定数aの値を求めよ。

（２）　の値を求めよ。

（３）　Xの平均値mと分散σ²を求めよ。

【解】

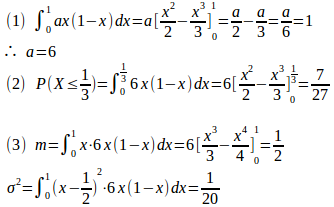
（解答終了）

（２）　正規分布

確率変数Xの確率分布が

　　

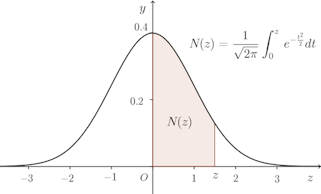
であるとき、Xの確率分布は正規分布であるといい、であらわす。

特に、平均が0、標準偏差1の正規分布
　　

を標準正規分布という。

ここで、mはXの平均値、σは標準偏差である。

　　

で、区間が区間にうつるとき、
　　








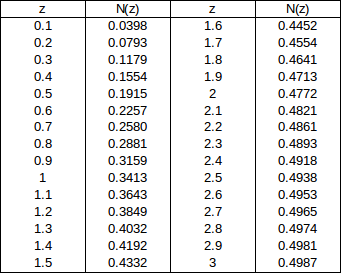
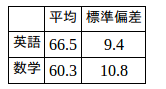
問題４　ある学年の英語と数学の成績が右表であるとき、英語７６点、数学７３点とった生徒は、どちらの科目のほうが学年の中で上位であると考えられるか。

【解】

英語の標準測度

　　

数学の標準測度
　　

したがって、数学のほうが上位である。

（解答終了）

 

問題５　あるクラスの成績Xの平均点をm、標準偏差をσとし、Xはほぼ正規分布をなすとき、成績をm−1.5σ、m−0.5σ、m+0.5σ、m+1.5σを境として５つの階級にわかち、成績のよい順にA、B、C、D、Eをつけるとき、かくかいきゅうにはいる生徒の割合を％で示せ。また、この場合、成績の平均は71.4、標準偏差を8.2とすると、成績が８７点、７４点、５６点のものはどの階級に入るか。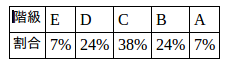

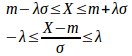
【解】
　　

であるから、

　　

と置くと、
　　

となる。

したがって、
　　

また、

　　

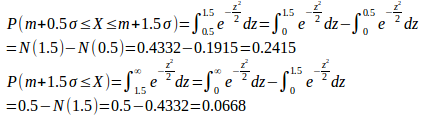
したがって、各階級の人数の割合は次のようになる。

 

m=71.4、σ=8.2のとき、

　　

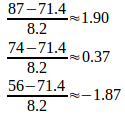
だから、８７点はA、７４点はC、５６点はE。

（解答終了）

 

§５　２項分布と正規分布の関係

二項分布に従う確率変数Xは、nが大きいとき正規分布に従うと考えられる。

したがって、

　　

は正規分布にしたがうと考えてよい。

問題５　さいころを１８００回投げるとき、１の目が出る回数Xが２７０から３３０回までの間にある確率を求めよ。

【解】
　　

Xは二項分布に従うから、Xの平均値mと標準偏差は

　　

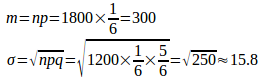
ｎが大きいから、Xは正規分布に従うと考えて、標準化すると

　　

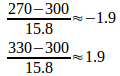
したがって、

　　

よって、求める確率は0.94。

（解答終了）

６　母平均の推定（区間）

大きさnの標本平均の分布は、母集団の平均（母平均）m、標準偏差の正規分布と考えられる。

したがって、

平均値mの信頼度９５％の信頼区間は

　　

平均値mの信頼度９９％の信頼区間は

　　

である。

ここで、は標本の平均である。

（σが未知のとき、標本の標準偏差sをσの代わりに用いる）

問題６　大きさ１００の標本の標本平均は56.3で標本標準偏差は10.2である。このとき、母平均mの信頼区間を９５％で求めよ。
【解】

問題の条件より、n=100、。

また、標本の大きさnが１００と大きいので母集団の標準偏差σは

　　

したがって、
　　

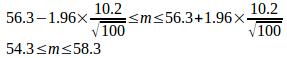
（解答終了）

 

§７　検定

「母平均がmである」という仮説を立てた場合、母集団から任意に抽出した大きさnの標本平均がならば、まず

　　

を求め、

①両側検定

　　優位水準９５％のとき、｜z｜≧1.96のとき仮説を棄却する。

　　優位水準９９％のとき、｜z｜≧2.58のとき仮説を棄却する。

②片側検定

　　優位水準９５％のとき、z≧1.65（右側検定）、z≦−1.65（左側検定）のとき仮説を棄却する。

　　優位水準９９％のとき、z≧2.33（右側検定）、z≦−2.33（左側検定）のとき仮説を棄却する。

問題７　A県のC市で高校３年生男子の中から１００名を任意抽出して平均身長を求めたところ169.8cmであり、またその標準偏差は5.8cmであった。

これは、A県における高校３年生男子の平均身長168.6cmよりも高いと判定されるか。

優位水準９５％と９９％の検定でそれぞれ判定せよ。

【解】

「C市の高校３年生男子の平均身長は168.6cmである」という仮説を立てる。

　　

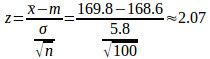
優位水準９５％の片側検定では、z=2.07>1.65だから仮説は棄却されて、C市の高校３年生男子の平均身長が高いと判定される。

優位水準９９％の片側検定では、z=2.07<2.33だから仮説は棄却されず、C市の男子の平均身長が高いとは認められない。

（解答終了）

タグ：統計