無限大、無限小などの問題

無限大、無限小などの問題

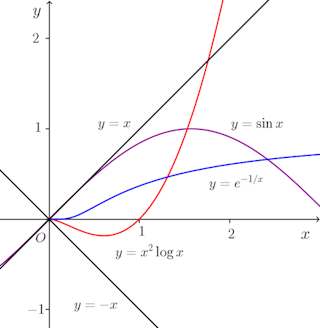
問題１　x→0+0のとき、次の無限小を小さい方から順に並べよ。

　　

【解】

　　

だから、sinxはxと同位の無限小。

　　

よって、x²logxはxより高位の無限小。

x=0のごく近くでは

　　

だから

　　

t=1/xとすると、x→0+0のときt→+∞だから

　　

したがって、はx²logxよりも高位の無限小である。

以上のことより

　　

の順である。

（解答終了）

定数倍の違いを無視したとき、高位の無限小は低位の無限小よりも早く０に収束する。

このことは、右のグラフをよくわかると思う。

ちなみに、y=xはy=sinxのx=0における接線である。

 

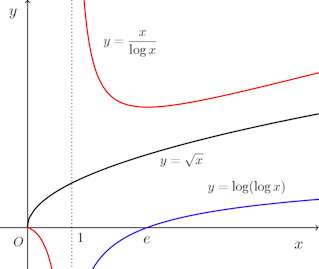
問題２　x→∞のとき、次の無限大を小さい順から並べよ。

　　

【解】

　　

よって、√xはx/logxよりも低位の無限大。

　　

だから、log(logx)は√xよりも低位の無限大。

したがって、

　　

（解答終了）

感覚的に言うと、これはどちらが早く、勢い良く±∞に発散するかを考えればよい。

微妙ですが、グラフを見ると、このことがわかるのではないか。

ちなみに、ロピタルの定理を使うと

　　

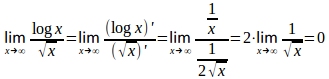
ロピタルの定理を使わないのならば、t>0とし

　　

また、x>eのとき、log(logx)>0、logx<xだから

　　

したがって、ハサミ打ちの定理より

　　

になる。

 

問題３　次の関数のx→0のときのxに対する無限小を求めよ。

　　

【解】

　　

よって、２位の無限小である。

（解答終了）

ランダウ記号（Landauのo）を用いて解くと次のようになる。

【別解】

マクローリン展開より

　　

したがって

　　

よって、xに対する２位の無限小である。

（別解終了）

上の計算では次のランダウ記号の演算規則を使用している。

　　

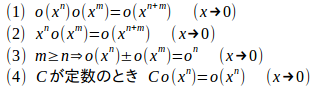
問題４　マクローリンの定理を使って次の極限を求めよ。

　　

【解答】

（１）　マクローリンの定理より

　　

したがって、

 　　

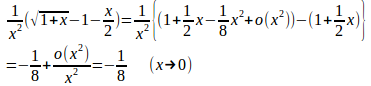
（２）　マクローリンの定理より

　　

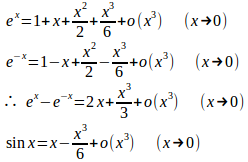
よって、

　　

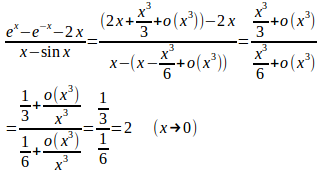
（解答終了）

タグ：微分積分 極限