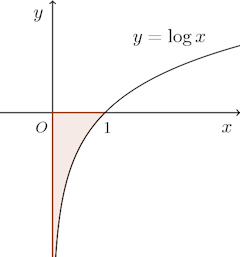ネムネコ 中学の2次関数の総合問題を作るの解答例 [ネコ騙し数学]
ネムネコ 中学の2次関数の総合問題を作るの解答例
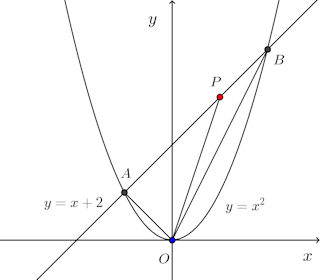 問題 2次関数y=x²と直線y=x+2がある。このとき、次の問いに答えよ。
問題 2次関数y=x²と直線y=x+2がある。このとき、次の問いに答えよ。
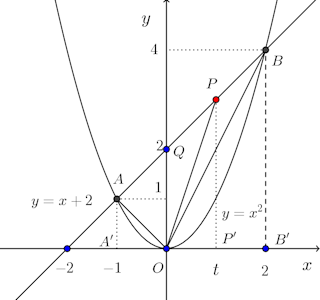
(2) 2次関数y=x²と直線y=x+2の2つの交点のうちx座標の小さい交点を点A、大きい方を点Bとし、原点をOとする。△OABの面積を求めよ。
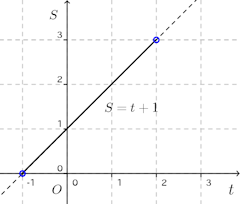
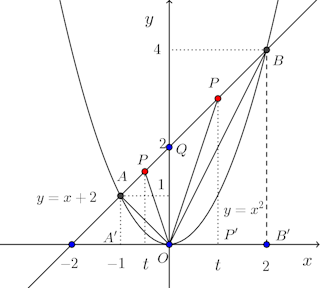
(3) 点Pは線分AB上にある。点Pのx座標をtとするとき、△OAPの面積Sを求めよ。また、横軸にt、縦軸にSをとり、そのグラフを書け。ただし、点PはA、Bと異なる点とする。(4) 線分ABの流さを求めよ。
【解答例】
(1) 2次関数y=x²と直線y=x+2の交点のx座標をxとすると、
(3) 問題の条件より、−1<t<2。
点A、点Bからx軸に下ろした垂線の足をそれぞれA'、B'、点Pからx軸に下ろした垂線の足をP'とする。AA'、PP'、そして、BB'は平行だから
穴あきの丸、◯は含まない。
(4) 三平方の定理より
−1<t<0のとき
t=0のとき
0<t<2のとき
ちなみに、△OABは∠OAB=∠Rの直角三角形。
何故ならば、直線AOの方程式はy=−xで直線の傾きは−1、直線y=x+2の直線の傾きは1で、2直線の傾きの積が(−1)×1=−1で、この2直線が直交するから。また、
と3平方の定理が成立することからもこのことが確かめられる。
そして、この結果を使うならば、△OABの面積は
ネムネコ 中学の2次関数の総合問題を作る!! 解いてミソ [ネコ騙し数学]
ネムネコ 中学の2次関数の総合問題を作る
中学の2次関数の問題を作ってみたにゃ。
 問題 2次関数y=x²と直線y=x+2がある。このとき、次の問いに答えよ。
問題 2次関数y=x²と直線y=x+2がある。このとき、次の問いに答えよ。
(2) 2次関数y=x²と直線y=x+2の2つの交点のうちx座標の小さい交点を点A、大きい方を点Bとし、原点をOとする。△OABの面積を求めよ。
(3) 点Pは線分AB上にある。点Pのx座標をtとするとき、△OAPの面積Sを求めよ。また、横軸にt、縦軸にSをとり、そのグラフを書け。ただし、点PはA、Bと異なる点とする。
簡単な問題だろう。
解いてミソ。
オマケとして、もうひとつ、小問を追加。
(4) 線分ABの流さを求めよ。
計算が大変なものになるかどうかは、ひとえに、数学的センス、図形的・幾何学的センスに関わっていると思うにゃ。
いかに簡単に解くか、腕の見せ所だにゃ。
答えを寄せてくれたら、清書して、このブログに掲載するにゃ。
だから、頑張ってといて欲しいにゃ。
誰も寄せてくれないのはわかっているけれど(^^)
第1回 広義積分とは [ネコ騙し数学]
第1回 広義積分とは
§1 広義積分の定義
これまで有界閉区間において連続な関数の積分について述べてきたが、たとえば、次のような積分を考えてみる。
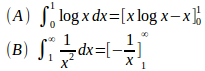 しかし、
しかし、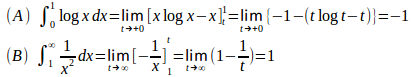
と考えることにより、その値を定めることができる。
このように拡張された積分を広義積分という。a、b(a<b)を実数、f(x)をa<x≦bで定義された関数とする。a<a'<bの任意の実数a'に対して、f(x)はa'≦x≦bで積分可能であるとする。このとき、
が有限に存在するならば、この値を
とあらわし、広義積分は収束するという。または、f(x)はa≦x≦bで広義積分可能という。すなわち、
と定義する。
f(x)がa<x<bで定義されていて、任意のa'、b'(a<a'<x<b'<b)に対してa'≦x≦b'で積分可能であるとき、適当なc(a<c<b)をとり、広義積分を
と定義する。
また、f(x)がa≦x<∞で定義され、b>aである任意のbに対して、a≦x≦bで積分可能で
とあらわし、広義積分は収束する、または、f(x)はa≦x<∞で広義積分可能であるという。
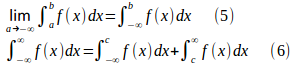
と定義する。
広義積分が収束するとき、広義積分
は絶対収束するという。
広義積分は収束するが、広義積分
が収束しないとき、広義積分
は条件収束するという。
§2 広義積分の計算例
問題1 次の広義積分の収束、発散を調べ、収束するものはその値を求めよ。
【解】
(1) だから広義積分。
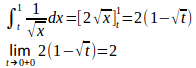
と収束するので、
(2) だから広義積分。
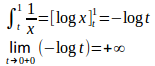
となり、発散する。
(3) t>1とすると
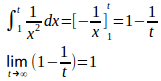
と収束するので、
(4) t>1とすると
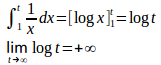
と発散する。
(解答終了)
問題2 次の広義積分を求めよ。
【解】
(1) t>0とすると、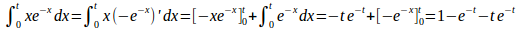
ロピタルの定理より
(2) だから広義積分。
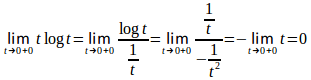
よって、
(3) となり、広義積分。
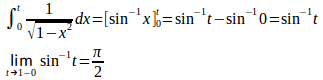
したがって、
(解答終了)