f(x)の導関数f'(x)が奇関数のとき、f(x)は偶関数か？の解答（怪答）

【お前らに質問！！】　f(x)の導関数f'(x)が奇関数のとき、f(x)は偶関数か？の解答（怪答）

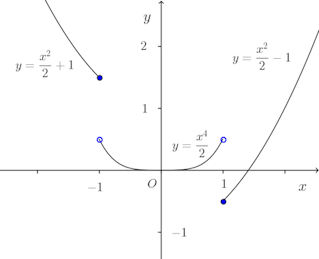
【反例】

　　

とする。

この関数f(x)の導関数f’(x)は

　　

となり、f'(x)は奇関数。

 

私は、f'(x)が連続であるとも、f(x)が実数全域で微分可能だとも言っていません。ただ、f(x)の導関数f'(x)が奇関数だ、y=f'(x)のグラフが原点対称だと言っただけですよ(^^ゞ
そんな条件は上の命題の中のどこにも書かれていない！！

「この質問は引っ掛けだ。卑怯だ！！」

反論、ごもっとも。

しかし、関数のグラフが繋がっていること、関数が連続であることの大切さがわかったんじゃないですか(^^)

そして、
今日ほど、この曲がふさわしい日はないのではないでしょうか♪




あまり挑発的なことを書いて、反感を買うといけませんから、すこしご機嫌取りを。




「いつもあなたの味方です」のネムネコです。

ねむねこ幻想郷の皆さんにお尋ねしますが、 f(x)の導関数f’(x)が奇関数ならば、f(x)は偶関数か？

ねむねこ幻想郷の皆さんにお尋ねしますが、
f(x)の導関数f’(x)が奇関数ならば、f(x)は偶関数でしょうか？

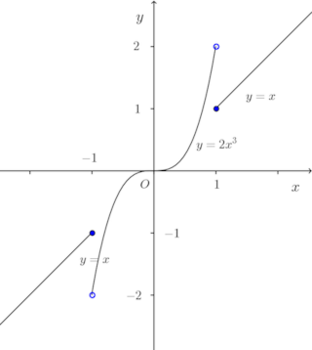
例えば、

　　

ならば、

　　

となる。

これはf(−x)=f(x)が成立するから、f(x)は偶関数。

また、

　　

のとき、

　　

だから、このときもf(−x)=f(x)が成立する。

次の命題は正しそうな臭いがいがプンプンする。

命題

f(x)の導関数f’(x)が奇関数ならば、f(x)は偶関数である

 

さて、この命題は正しいか。

正しければ証明を、正しくなければ反例をあげよ。

ちなみに奇関数とは

　　

が成立する関数。

偶関数は

　　

奇関数の代表的な例としてf(x)=x、偶関数の代表例はf(x)=x²がある。

タグ：微分積分

第７回 ベータ関数入門１

第７回　ベータ関数入門１

p>0、q>0のとき、

　　

が絶対収束することを証明する。

【証明】

p≧1、q≧1のとき、通常の積分である。

そこで、

　　

と分けて考える。

0<p<1のとき、

　　

だから、

　　

は広義積分である。

また、0<q<1のとき

　　

だから、

　　

は広義積分である。

0<p<1のとき、0≦x≦1/2とすると、1/2≦1−x≦1である。

q>1のとき、

　　

0<q<1のとき

　　

である。

以上のことより、q>1、0<q<1のいずれであろうと、

　　

であり、

　　

0<p<1のとき、t>0とすると、
　　

だから、広義積分

　　

は絶対収束する。

次に

　　

を考える。

0<q<1とする。

1/2≦x≦1とする。

p>1のとき、

　　

0<p<1のとき

　　

いずれにせよ

　　

したがって

　　

0<t<1とすると
　　

したがって、広義積分

　　

は絶対収束する。

以上のことより、p>0、q>0のとき

　　

は絶対収束し、

　　

は絶対収束する。

（証明終了）

なお、上の証明では次の定理を使っている。

定理２（比較判定法）

関数f(x)、g(x)は(a,b]で不定積分をもち、

　　

であるとする。

このとき広義積分が収束すれば、広義積分も収束する。

区間[a,b)、[a,∞)、(−∞,b]についても同様である。

ベータ関数の定義

p>0、q>0に対して

　　

で定義されるB(p,q)をベータ関数という。

さて、x=sin²θとおくと、

　　

だから
　　

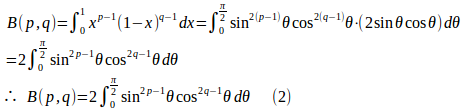
また、
　　
とおくと、

　　

したがって、
　　

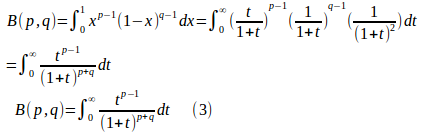
とベータ関数B(p,q)を定義することができる。

問　次の広義積分の値を求めよ。

　　

【解】

　　

だから、（２）式にp=1/2、q=1/2を代入すると、
　　

（解答終了）

タグ：広義積分 微分積分