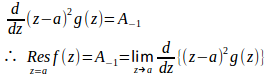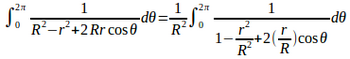あの積分に立ち返る [ネコ騙し数学]
あの積分に立ち返る
再び、次の積分に戻る。
何も考えずに、不定積分の公式に使えば
このような答案を試験の際に書くと、大学の先生は、決まって、「広義積分を理解していない」、「公式の濫用だ」と声高に叫ぶ。
そこで、ならばと、複素関数の積分の知識を使って次のように解いてみることにする。
実数で定義される1/xという関数を、次のように、複素数に拡張する。
そうすると、f(z)は0以外の複素平面上の全ての点で正則になる。
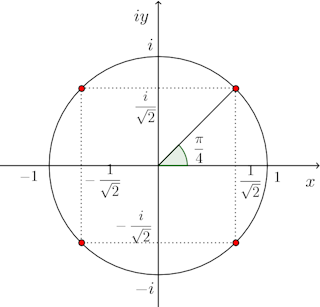
そこで、積分の経路を下図のように複素平面上にとることにする。
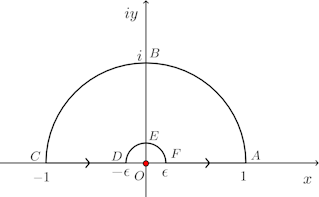
円弧ABCは半径1の円弧、円弧DEFは半径ε>0の円弧。
そうすると、円弧ABCと線分CD、円弧DEF、線分EAで囲まれた曲線の内部でf(z)は正則だから、この積分路にそった積分の値は0になる。つまり、
ところで、円弧ABCは半径1の円の半円だから
つまり、
大学の先生が声高に「公式の濫用」と叫ぶ公式⑨がよみがえる(^^ゞ
これまで、複素積分の定積分の応用でやってきたタイプⅡ、タイプⅢ、ジョルダンの補助定理、さらに、
この手法が胡散臭い(?)ことを知っていながら、確信犯的に⑨の公式(と同じ手法)を使って講義を受けている学生達を幻惑することが多いのだから、なお、質(たち)は悪くて、その罪は重い。万死に値すると言ってもいい(^^ゞ
⑨の能力を過信しすぎだケロ。⑨にそんなことがわかるはずがないにゃ。⑨の能力を舐めてはいけないにゃ。ないことをあることに、あることをないことにし、禁則、タブーを平気で犯すのが⑨であり、その上をゆく⑨³なのだから。
高木貞治の『解析概論』(岩波書店)には次のように書いてある。
(註:一部編集)ε、ε’は独立である。
たとえば、[−1,1]内でx=0において1/xは不連続でここでε=ε’とすれば
となるけれど、は0であることを意味しない。
それは
であるべきだが、この極限は存在しない。故に
は無意味である。それは収束しない(発散する)。
上記において
が存在しなくても、もしも独立変数ε、ε’の間に特別の関係を付けるならば上の例のように極限値が存在することもある。特にε=ε’とするときの極限値をCauchyは
の主値(value principle)と名づけた。Cauchyは虚数積分の考察(解析函数論の前身)において、そのような極限値に遭遇したのであった。現今でも、文献において、積分の主値なる語が上記の意味で、かりおり、用いられる。
(3)の極限が存在しないことは、たとえば、ε=2ε’とすれば、(3)の値はlog2となり、log1、つまり、0とは違った値になる。ε、ε’の0への近づき方によって極限値が異なってしまい、極限値が1つの値に定まらないことから明らか。
第2回 三角形の合同条件 [ネコ騙し数学]
第2回 三角形の合同条件
小中学校で、次の3つの三角形の合同条件を習ったと思う。
今回は、前回、導入した公理に基づいた証明を紹介する。定理6 三角形の合同条件
(1) 2辺と挟角相等(2) 1辺と両端の角相等
(3) 3辺相等【証明】
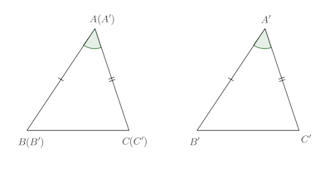 (1) △ABCと△A’B’C’において、AB=A’B’、AC=A’C’、∠A=∠A’とする。
(1) △ABCと△A’B’C’において、AB=A’B’、AC=A’C’、∠A=∠A’とする。△A'B'C'を移動させ、AとA’が一致するように、半直線ABとA'B’を重ねる。
AB=A'B'だから、BとB'は重なる。また、∠A=∠A’だから、半直線ACとA’C’も重なり、AC=A'C'だから、CとC’は重なる。
2点B(B')とC(C')を通る直線は1本なので、BCとB'C'は重なる。よって、
△ABC≡△A’B'C'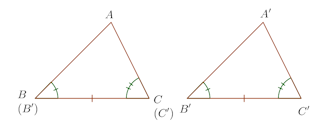 (2) △ABC、△A’B’C’において、BC=B’C’、∠B=∠B’、∠C=∠C’とする。
(2) △ABC、△A’B’C’において、BC=B’C’、∠B=∠B’、∠C=∠C’とする。
∠B=∠B’、∠C=∠C’であるから、B’A’とBAが重なり、C’A’もCAに重なる。
2直線の共有点は1だけだから、A’とAは重なる。よって、△ABC≡△A’B’C’である。
(証明終わり)(3)のの証明のために次の定理を証明する。
定理7 二等辺三角形の底角は等しい。
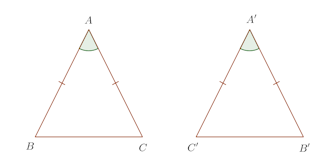 【証明】
【証明】△ABCを裏返して、A、B、CがA’B’C’になったとする。
図形を裏返しにしても形や大きさは変わらないから△ABCと△A’C’B’においてAB=AC=AC’
AC=AB=A’B’∠BAC=∠C’A’B’
よって、△ABC≡△A’C’B’ (二辺挟角相等)∴ ∠ABC=∠A’C’B’=∠ACB
(証明終わり)そして、この定理7を用いて、定理6の(3)を証明することにする。
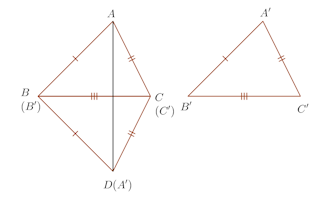 定理6の(3)の証明
定理6の(3)の証明BC=B'C'だから、△A'B'C'を移動してB’とB、C'とCとを重ねると、辺B'C'と辺BCは重なる。
そこで、A'が直線BCに関してAと反対側にくる点をDとする。△BDAはBD=BAの二等辺三角形なので、∠BDA=∠BAD。
また、△CADもCA=CDの二等辺三角形なので、∠CAD=∠CDA。よって、∠BAD=∠BDA。
定理6の(1)の2辺挟角相等より、△ABC≡△DBC。∴ △ABC≡△A'B'C'
(証明終)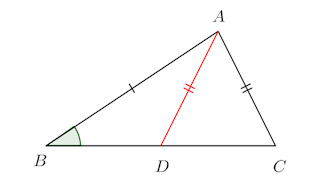 問題 「AB=A'B'、AC=AC'、∠ABC=∠A'B'C'ならば△ABC≡△A'B'C'である」は正しいか。
問題 「AB=A'B'、AC=AC'、∠ABC=∠A'B'C'ならば△ABC≡△A'B'C'である」は正しいか。【解】
反例として、次の三角形を上げれば十分でしょう。つまり、正しくない。
(解答終)ネムネコ、Bloggerにアニメーション付きの幾何の問題をアップ!! [ネコ騙し数学]
幾何の問題(アニメーション付き)
http://nemneko.blogspot.jp/2017/02/blog-post_31.html
次のような問題。
問題
定まった二等辺三角形ABCの底辺BC上の1点をPとし、等辺AB、AC上にそれぞれ点Q、Rをとり、BQ=CP、CR=BPとなるようにすれば、△PQRは底辺BC上の点Pの位置にかかわらず、頂角の大きさが一定な二等辺三角形になることを証明せよ。
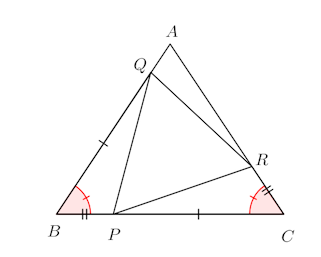
簡単な問題だから秒殺ものでしょう。
見た瞬間に答えがわかる人は、点Pが点Bを出発し点Cに向かうとき、線分QRの中点Mの軌跡などを求めて欲しいにゃ。
きっと秒殺できる問題だから、解答なんて野暮なものは不要でしょ(^^)
アニメーションを見たい人は、上記アドレスにアクセスして欲しいケロ。
このアニメーションを見れば、一定の頂角が何になるかは一目瞭然だケロ。
解きやすいスペシャル・ケースから一定値を推測するということは重要なことだと思うにゃ。
この問題の場合、PがBやC重なるとき、さらに、Pが線分BCの中点に達した時など。一定の頂角を教えたようなものだね(^^)
第58回 留数定理の定積分への応用 問題編3 [ネコ騙し数学]
第58回 留数定理の定積分への応用 問題編3
タイプⅢ
f(z)は複素平面の上半平面Imz≧0で有限個の極を除いて正則であり、
または
とする。
このとき、
f(x)が偶関数のとき
f(x)が奇関数のとき
問題1 次の定積分を求めよ。
留数を求めると、
この問題は、上の公式を使わずとも、次のように計算することができる。
【別解】
とおく。
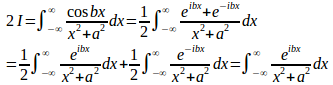
だから、
だから、
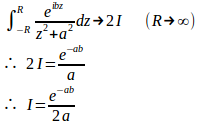
(別解終)
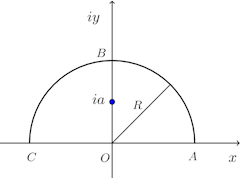
問題2 a>0、b>0のとき、次の定積分の値を求めよ。
【解】
(1)
また、
(2)
また上半平面に2位の極z=iaをもち
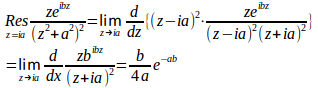
(3)式より
ねこ騙し流「アキレスと亀」 [ネコ騙し数学]
ねこ騙し流「アキレスと亀」
アキレスと亀という有名な話がある。
足の速いアキレスと足の遅い亀が走り競争することになった。
同一地点から同時に出発したならば勝負の結果は、誰の目にもあきらかだ。そこで亀はハンディキャップをもらう。そして、ヨーイドン!!
亀がいた地点にアキレスが達したとき、亀は前を行っている。そして、その地点にアキレスが達したとき、亀はさらにその先を進んでいる。その地点にアキレスが達したとき、亀はまだ前にいる。・・・。
したがって、アキレスはいつまで経っても(?)亀に追いつけないというお話。
ゼノンのパラドクスとも呼ばれるお話。
この反論として、次のようなものをあげることができる。
亀のハンディキャップをH、アキレスの走る速さをV(m/秒)、亀の走るv(m/秒)とする。仮定よりV>m。
出発後に、アキレスが亀に追いつく時間をT秒とすると、次のような方程式が成り立つ。
あ〜、なるほどと思ってはいけない。
与えられている条件は、1 亀がハンディキャップをもらうということ
2 アキレスの走る速さは亀のそれより速いという2点だけだからだ。
アキレスの走る速さと亀の走る速さが一定という条件はどこにも加わっていない。にもかかわらず、この仮定を勝手に加えているのだから。
そこでだ、アキレスの走る速さは一定Vで、亀の走る速さvを次のようにするにゃ。
tはヨーイドンからの時間(秒)とする。記号max(a,b)はaとbの小さくない方の値。
このとき、t>0で常に
そして、t秒後のアキレスの位置Xは、スタート地点を0とすると
の場合は
となり、どちらの場合も、亀がアキレスに抜かれることはない。
亀の走る速さは限りなくアキレスの走る速さに近づくけれど、アキレスの速さよりは遅い。
そして、アキレスと亀の距離は限りなく0に近づくけれど、アキレスが亀に追い付き、追い越すことは起きない。
ただ、この記事を読んで、「ゼノンの主張が正しい」と誤解しないで欲しい。
ここで言いたのは、条件次第でゼノンの主張を否定することも肯定することもできるということだ。
問題が曖昧すぎて、これだけでは真偽が定まらないということだケロよ。
広義積分のおまけ [ネコ騙し数学]
広義積分のおまけ
問題1 次の等式を証明せよ。
t=tanxとおくと
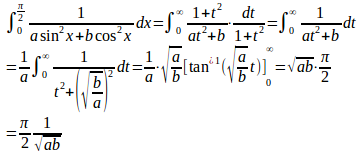
(解答終了)
こう解けば、複素積分や留数定理を使わずに、実積分の広義積分としてこの値を求めることができる。
ちなみに
これで終わると、手抜き呼ばわりされるかもしれないので、もうひとつ広義積分の問題を解くことにする。
問題2 次の積分の値を求めよ
この不定積分は次のように求められる。
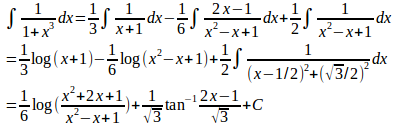
したがって、
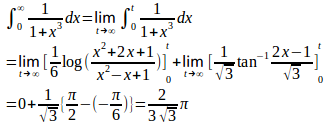
(解答終了)
すこし補足説明すると、
そして、問題1、2とも積分公式
どこから、x²+2x+1が出てきたかですが、これは
この程度の積分ならば、実積分、つまり、微分積分の範囲で解くことができるという話です。
なお、昨日紹介した複素積分による手法で問題2の積分の値は求められないので、この点は注意すること。第57回 留数定理の定積分への応用 問題編2 [ネコ騙し数学]
第57回 留数定理の定積分への応用 問題編2
タイプⅡ
このとき、
特に、f(x)が偶関数のとき、
問題1 次の積分の値を求めよ。
何故ならば、|z|=Rを十分大きく取ると
で、f(z)の上半平面の極はの3点であるから。
極は1位の極だから、留数は
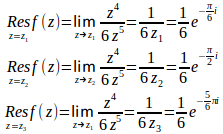
したがって
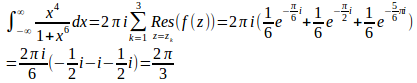
(解答終了)
留数の計算には
この問題の場合、h(z)=z⁴、g(z)=z⁶+1として計算している。
また、|z|>1のとき
ちなみに、
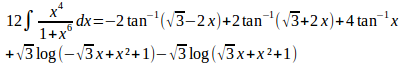
となるので、この不定積分の結果を利用し
問題2 次の定積分の値を求めよ。
(1)
(別解)
(2) この積分もタイプⅡの条件を満たす。
したがって、留数は
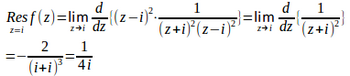
f(z)は偶関数だから、留数定理より
なぜ、f(z)に(z−1)²をかけて微分をすると留数が求まるかですがこれはこういう仕組み。
f(z)がz=aの2位の極をもつとすると、この関数のローラント展開の主要部は
m(m>1)位の極を持つ場合、
第56回 留数定理のの定積分への応用の問題編1 [ネコ騙し数学]
第56回 留数定理のの定積分への応用の問題編1
定理(留数定理)
関数f(z)が単一閉曲線Cを境界とする領域に有限個の孤立特異点を持ち、これら以外では境界Cも含めて正則であるとき、
タイプⅠ
ここでf(X,Y)はX,Yの有理関数。
と置くと、
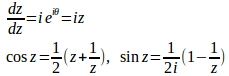
となり、[0,2π]は単位円周|z|=1に移るから、
問題1 次の定積分の値を求めよ。
とおくと
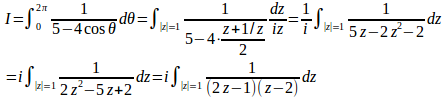
ここで、
したがって、留数は
留数定理より
だから、
問題2 次の定積分を求めよ。
とおくと
ここで、
したがって、f(z)の留数は
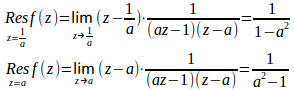
|a|<1のとき、単位円|z|=1の極はz=aのみだから
留数定理より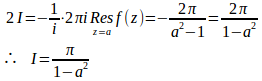
|a|>1のとき、単位円|z|=1の極はz=1/aのみだから
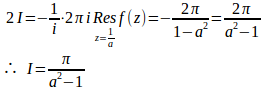
この2つの結果をまとめて
問題3 0<r<Rとするとき、
を求めよ。
【解】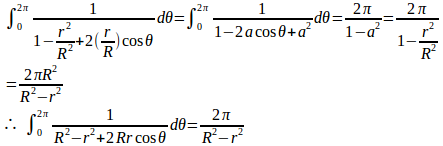
(解答終了)
問題4
【解】
a=bのとき
三角関数の倍角公式より
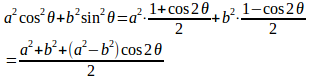
したがて、
(解答終了)
問題4は、とおいて解くのが一般的だろうが、こうすれば実積分として積分の値を求めることができる。
複素積分の補足説明(留数を求める方法) [ネコ騙し数学]
複素積分の補足説明(留数を求める方法)
複素解析のところで、留数定理の定積分への応用の具体例についてほとんど述べなかったので、これを明日以降、3回ほどやることにして、その序言のかわりとして、復習をかねて、前回取り上げた問題を例に、留数を求める方法について簡単に説明することにする。
z=aが複素関数f(z)の特異点で1位の極のとき、z=aのまわりでのローラン展開は
また、g(z)がz=aを1位の零点をもつ正則な関数。h(z)をz=aを零点にもたない正則関数とするとき、
g(z)、h(z)をz=aまわりにテーラー展開するとき
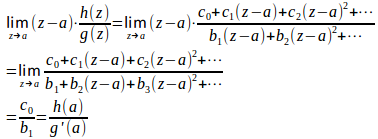
だから。
さらに、補足説明をすると、
複素関数
で、
そこで、
この点を複素平面(ガウス平面)上に描くと右の図のようになる。
しかし、この解を次のように求めることも可能。
何故だろうか(^^)
話を、留数の計算に戻す。
g(z)=z⁴+1の零点はどれも1位。
何故ならば
そして、複素平面の上側にある点はの2点のみ。
第17回 ベータ関数と複素解析の留数定理を使って定積分を計算する [ネコ騙し数学]
第17回 ベータ関数と複素解析の留数定理を使って定積分を計算する
ベータ関数の定義
(1)式は、
特に、p+q=1のとき
一方、複素解析、複素積分の留数定理とは次の定理である。
定理 (留数定理)
関数f(z)が閉曲線Cの内部に有限個の特異点をもち、これらの点以外では曲線C上およびその内部で正則であるとき、次の等式が成り立つ。
複素解析で扱う関数は、実数の変数ではなく複素数の変数であることに注意。そして、iは虚数単位i²=−1である。
また、f(z)のz=α近傍でのローラン展開
の係数A₋₁をz=αにおける留数といい、または
であらわす。
問題 次のことを示せ。
t=1/xとおくと、x=0のときt=∞、x=∞のときt=0。
また、
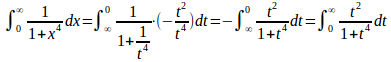
したがて、
さらに、
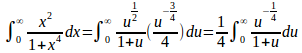
(3)式でp=3/4とおくと
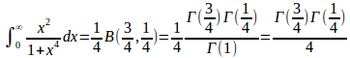
ガンマ関数の倍角公式から
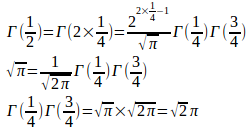
したがって、
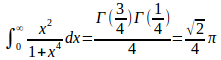
(解答終)
複素解析の留数定理を使うと次のように積分の値を求めることができる。
【留数定理を使った解答】
の複素平面の上半平面にある極はの2つ。
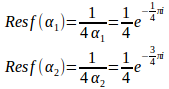
f(z)は偶関数だから
(解答終了)
なお、留数を求める計算では、
g(z)をαを1位の零点としてをもつ正則関数、h(z)をαを零点にもたない正則関数とするとき、
上の問題の場合、g(z)=1+z⁴、h(z)=z²だから
そして、この問題の関数は、複素解析の第53回で述べたタイプⅡの積分。
タイプⅡ
f(z)は複素平面の上半平面(Imz≧0)で有限個の極を除いて正則であり、実軸上に極を持たず、かつ
とすると、
特に、f(x)が偶関数のとき、
ガンマ関数の倍角公式
の導出は、前回の記事で示してある。