複素数を用いて極座標における速度、加速度を求める

複素数を用いて極座標における速度、加速度を求める

平面上を移動する動点Pの時刻tにおける位置ベクトルをrとすると、速度ベクトルv、加速度ベクトルaは次式で与えられる。

　　

平面の基本ベクトルを、また、時刻tにおける点Pの座標を(x,y)とすれば、

　　

となるので、
　　

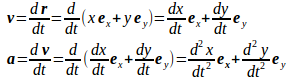
である。

速度ベクトルと加速度ベクトルを

　　

とあらわせば、
　　

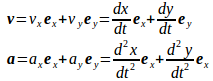
から、

複素数zは、その実部をx、虚部をy、さらに虚数単位をi（i²=1）とすると、z=x+yiで表される。

そして、横軸に実軸、縦軸に虚軸をとると、複素数z=x+yiは右の図で示される。

右図を見ると、複素数が平面ベクトルと同等のものであることがわかると思う。

この手法を用いれば、

　　

と速度ベクトル、加速度ベクトルを簡潔に表現できる。

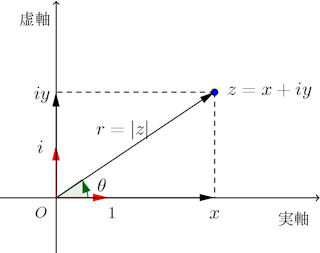右図に示すように、原点Oと点zと結ぶ線分と実軸のなす角度（反時計回りを角度の正の向きとする）θ、原点Oと点zとの線分の長さを

　　

で定義することにする。

そうすると、zの実軸の成分x、虚軸の成分yは

　　

となる。

つまり、

　　

となる（極形式）。

これをオイラーの関係

　　

で書き換えると、

　　

となる。
　　

これをtで微分すると、

　　

ここで、記号「・」はtによる微分

　　

をあらわす。

は大きさが１でと方向が同じベクトルと考えることができる。

また、

　　

ベクトル(cosθ,sinθ)とベクトル(−sinθ,cosθ)の内積を取ると

　　

となり、は直交している。

そして、その大きさは

　　

で１。

も大きさが１だから、互いに直交する単位ベクトルを元にした座標系を作ることができる。

この新たな座標は何かといえば、対応規則からあきらかなように、極座標！！

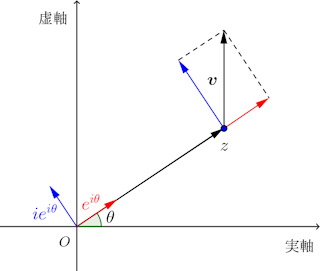
そこで、

　　

をもう一度見なおすと、速度ベクトルvの基本ベクトル方向の成分は、基本ベクトル方向の成分はということになる。

そして、速度ベクトルvをさらに微分すると、
　　

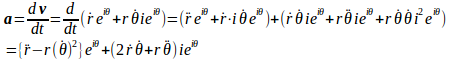
となることから、

　　

以上のことをまとめると、

極座標における速度、加速度のr方向、θ方向の成分は

　　

ここでは、が直交していることを内積を使って示したが、

　　

だから、はを９０°、π/2(rad)回転させたものであることはあきらか。

タグ：複素解析