多項式による補間

多項式による補間

§１　補間

２つの点の間に位置する点、すなわち、におけるf(x)の値を求めることを補間するという。２つの点の外の点におけるf(x)の値を求めることを補外するという。

もちろん、例えば、f(x)=x²+3x+2のように関数が式の形で与えられ、しかも、この計算が簡単にできる場合、補間や補外をする必要はなく、f(x)=x²+3x+2を用いて計算すればよい。しかし、f(x)=sinxならば、電卓などを使わない場合、値が既知の点をもとにテーラー展開などをして値を求めざるを得ない。

また、複数の点、たとえば、の値は与えられているけれど、y=f(x)の関数が与えられていないことも多く、何らかの手段で既知でない点の値を求めざるを得ない。

このような時に、補間や補外といった手法が使われる。

補間や補外には、テーラー級数がよく用いられる。すなわち、

　　

である。

と書くのは面倒なので、と書くことにすると、

　　

これを２次の項、すなわち、で打ち切ると、

　　

に前進差分を

　　

を用いると、

　　

になる。

ここで、

　　

とおくと、（２）は

　　

となる。

この（３）を１次補間公式という。

なにか難しいことを書いているように思うかもしれないが、（３）は、における値f(x)を２点を通る直線（線分）で近似したものに過ぎない。

（１）を３次の項で打ち切るときには、

　　

として、これを（１）に代入すると、
　　

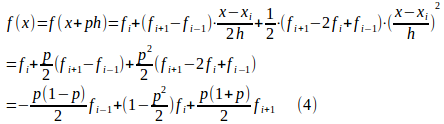
という２次補間公式が得られる。

例１　３点(0,1)、(1,−1),(2,3)があるとする。

　　

とすると、
　　

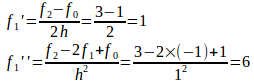
この結果を（１）に代入すると、

　　

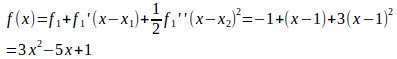
という補間曲線が得られる。

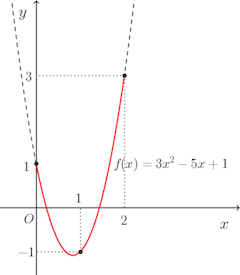そして、これが２次補間によって得られる曲線である。

もちろん、

　　

として、f(0)=1、f(1)=−1、f(2)=3としてえられる次の連立方程式を解いてもよい。

　　

この連立方程式の解は(a,b,c)=(3,−5,1)となり、同じ結果が得られる。

 

§２　ラグランジュ補間

次のn次の多項式を考える。

　　

この多項式は以外のすべての点

　　

において0である。

そこで、

　　

とおくと、多項式はにおいて1となり、それ以外ので0になる。

つまり、

　　

だから、

　　

とおくと、このn次の多項式はn+1個の点

　　

を通る多項式になる。

これがラグランジュ補間と呼ばれる方法である。

例２　３点(0,1)、(1,−1),(2,3)があるとする。

　　

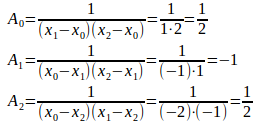
だから、

　　


問

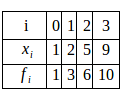
上の表の値をもとに、ラグランジュ多項式によってf(6)を補間せよ。

【解】

　　

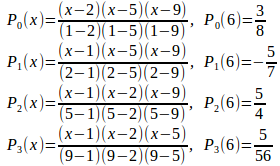
よって、

　　

（解答終了）

これが人間向きの計算法かと言えば大いに疑問であるが、単純な繰り返し計算を得意とするコンピュータにとっては都合のいい計算法である。

以下にこのサンプルプログラム（C言語）を示す。

#include <stdio.h>
#include <math.h>

double f(double x) {
return sin(x); // f(x)=sin x [−π,π]
}

// ラグランジュ補間
double lagrange(double *x, double *y, int n, double t) {
double p,s;
int i,j;

s=0;
for (i = 0; i <= n; i++) {
p = 1.;
for (j=0;j<=n; j++) {
if (i != j) {
p = p*(t-x[j])/(x[i]-x[j]);
}
}
s = s+y[i]*p;
}
return s;
}

main() {
double x[10]={0.0};
double y[10]={0.0};
double t,h;
int i;
int n = 9; //n次式
double a, b;

b = 4.*atan(1); // 区間[a,b]のbの値πをセット
a = -4.*atan(1); // 区間[a,b]のaの値−πをセット
h = (b-a)/n; // [a,b]をn等分した幅
for (i = 0; i <= n; i++) { // i=0〜nの点の値をセット
t = a+i*h;
x[i]= t;
y[i] = f(t);
}

// 計算結果の出力
printf(" x lagrange sin x \n");
for (i=0; i <=100; i++) {
t=a+i*(b-a)/100;
printf("%f %f %f\n",t, lagrange(x,y,n,t), f(t));
}
}

f(x)=sinx（−π≦x≦π）を５次のラグランジュ補間で近似計算した値を以下に示す。この場合、よく近似できていることがわかる。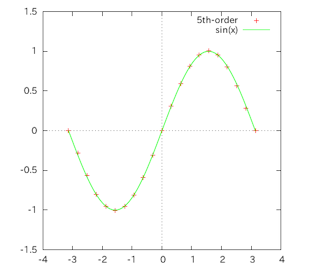

誤解がないように言っておきますが、与えられた点をすべて通る多項式を求めただけで、ラグランジュ補間などの（等間隔の）多項式補間が元の曲線を忠実に反映しているというわけではない。

例えば、

　　

という曲線があるとする。

これを[−1,1]で等間隔に５分割（点の数は６）、９分割（点の数は１０）し、その値をもとに５次補間、９次補間すると右のような曲線が得られる。

点が多く、高次で補間するほうがよりもとの曲線を反映するように考えられるが、この関数の場合、高次にすればするほど、端点であるx=±1の近傍でもとの曲線との乖離が大きくなる現象、ルンゲ現象が発生する。

直線で結んだほうがこの曲線の挙動を正確に反映している。

ここで言いたいのは、データがn+1個あるからn次の多項式で近似するということは非常に危険な行為だということです。

n次のラグランジュ多項式で結べば確かにのすべての点を通る曲線を得られるけれど、時に、このルンゲ現象のようなことが発生することがある。

また、この曲線の極値はx=0のところにのみあるにもかかわらず、５次補間では極値をとる点がが３、９次補間では極値をとる点が７になるなどの問題も発生する。

だから、物理や化学などの実験で得られたデータなどのグラフは、絶対に高次のラグランジュ補間で結んではいけない。

実験データを高次のラグランジュ補間で結んだグラフを書き、それをレポートなどにのせて提出すると、必ず、実験担当の先生や指導教官からこっぴどく叱られる。「このデータを曲線で結んだ理論的根拠は何だ。説明しろ！！」と問い詰められるのが落ちである。

タグ：数値解析