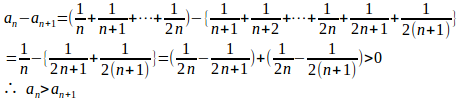高校数学の定積分 [ネコ騙し数学]
高校数学の定積分
高校数学の定積分の定義は、以下のようなものである。
関数f(x)は有界閉区間[a,b]において連続で、[a,b]を
例えば、[0,1]で定義されたf(x)=x²の定積分
（１）を使うと、次のような問題を解くことができる。
問題１ 次の極限値を求めよ。
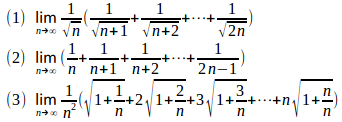
【解】
（１）
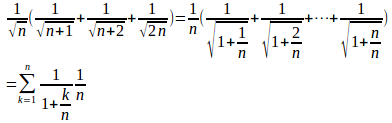
[0,1]をn等分し、
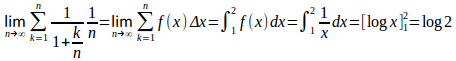
（別解）
[1,2]をn等分し 
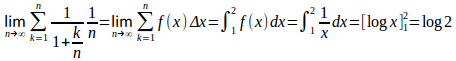
（２）
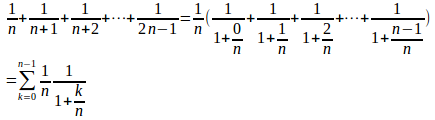
[1,0]をn等分し
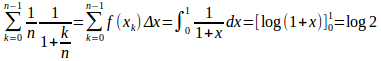
（別解）
[1,2]をn等分し
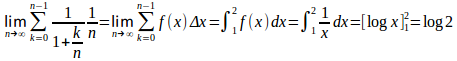
（解答終了）
（３）
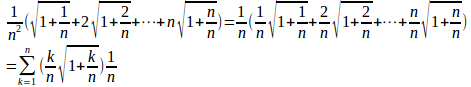
[0,1]をn等分し、
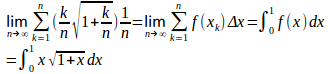
ここで、
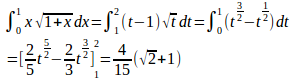
（解答終了）
問題２ f(x)=x⁴のとき、次の極限を求めよ。
【解】
[0,1]をn等分し 
という区間を考えると、
を
となるので、は点
を1:2に内分する点で、また、f(x)=x⁴は[0,1]で単調増加。
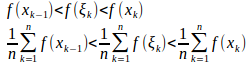
また、
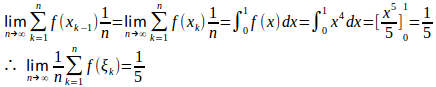
さらに、
となるから、
は
を2:1に内分する点。したがって、
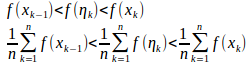
となり、同様に
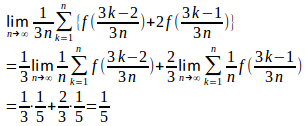
（解答終了）
（１）は、
の
や
としたものだが、問題２はのとり方によらず積分の値は一定で
関数の振幅 [ネコ騙し数学]
関数の振幅
定義
有界閉区間I=[a,b]上の有界な関数f(x)に対して
区間I上の関数f(x)がある実数Mがあり、すべてのx∈Iに対して
論理記号で書くと、
ちなみに、有界でない関数は、（２）の否定をとると、
有界な関数の例としては、たとえば、I=[0、1]で定義されたf(x)=x²。このとき、0≦f(x)≦1だから有界である。
一方、有界でない関数の例としては、たとえば、I=(0,1]で定義されたf(x)=1/x。この関数の値域は1≦f(x)<∞だから、有界ではない。現に、どのような実数M≧1を与えても
例１ I=[0,1]、f(x)=x²とすると、
例２ I=[−π,π]、f(x)=sin とすると。
例３ I=[−1,1]、
−1≦x<0のとき
0≦x≦1のとき
上限と下限の問題 Part２ [ネコ騙し数学]
上限と下限の問題 Part２
問題１
【解】
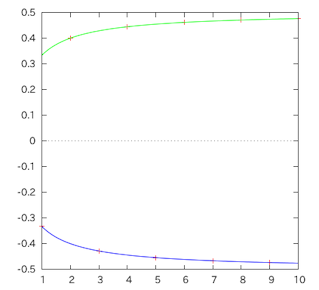nのときの集合Aの要素を 
nが偶数、n=2k（k=1,2,…）のとき
は単調増加列で
は単調減少列で
（解答終了）
問題２ 数列
に関して次のことを証明せよ。
（１） すべてのn∈Nに対して
したがって、
は数列
の上界。
（２） すべてのn∈Nに対して
よって、
は数列
の下界。
等号が成立しない例として、一般項が
である数列があげられる。
（解答終）
問題３
A、Bを実数Rの空でなく有界な部分集合として 
sup C = sup A + sup B
【解】sup A=α、sup =βとおく。
任意のx∈Aに対してx≦α、任意のy∈Bに対してy≦β。したがって、任意のx+y∈Cに対して、
また、αはAの上限だから任意の正数ε>0に対して
βはBの上限だから任意の正数ε>0に対して
よって、任意の正数ε>0に対して
よって、
sup C = sup A + sup Bである。
（解答終）上限・下限の問題 [ネコ騙し数学]
上限・下限の問題
問題を解く前に、最大数、最小数の定義を与える。
最大数・最小数の定義
Aを空でない実数Rの集合とする。α∈Rが、α∈AかつAの上界であるとき、αをAの最大数といい、max Aであらわす。
β∈Rが、β∈AかつAの下界であるとき、βをAの最小数といい、min Aであらわす。問題１
【解】
sup A = 1、inf A=−1、max A = 1。min Aは存在しない。
（解答終了）
問題２
Aを空でない実数Rの集合とする。max A（min A）が存在するための必要十分条件は、Aが上に有界（下に有界）であって、かつsup A∈A（inf A∈A）であることをを示せ。
【解】max A=αとする。αはAの上界だから任意のx∈Aに対してx≦αで、任意の正数ε>0に対してα−ε<α∈A。したがって、α=sup Aで、sup A∈Aである。
β=sup Aとすると、任意のx∈Aに対してx≦βでβ∈Aだから、β=max Aである。
min A=αとする。αはAの下界だから任意のx∈Aに対してx≦αで、任意の正数ε>0に対してα+ε>α∈A。したがって、α=inf Aで、inf A∈Aである。
（解答終了）
問題３ 次の集合の上限と下限を求めよ。
t∈(0,π]として、
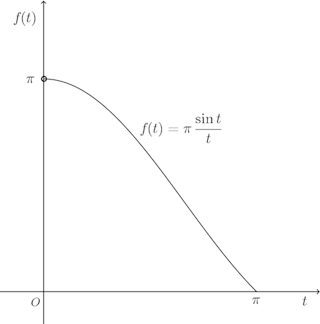とおくと、f(t)のグラフは右図になり、単調減少となる。したがって、f(t)の上限は
（解答終了）
問題４ 空でない実数Rの部分集合Aに対して
このとき、
ただし、−(−∞)=∞、−(∞)=−∞とする。
【証明】−Aが上に有界であるとする。
α=sup (−A)とおくと、すべての−x∈−Aに対してα≧−x。したがって、すべてのx∈Aに対してx≧−αとなり、−sup(−A)=−αはAの下界になる。inf AはAの下界の最大数だから、 
−Aが上に有界でないとすると、Aは下に有界でない。
すなわち、sup (-A)=∞、inf A=−∞。よって、
−(−A)=Aだから、（３）より
ちょっと解いてみた [ネコ騙し数学]
ちょっと解いてみた
問題 数列
が収束すること示し、その極限値が1/2と1の間にあることを示せ。
【解答】
したがって、数列
は単調減少。
だから
で、0はの下界。
下に有界な単調減少の数列は収束するので、は収束する。
が収束することはわかった。その極限値を求めることにする。
f(x)はx≧0で単調減少関数だから、
で
また、
で
だから、同様の議論から 
上限と下限 [ネコ騙し数学]
上限と下限
§１ 上界と下界
Aを実数Rの空でない部分集合とする。α∈Rが、任意のx∈Aに対し、α≧xであるとき、αをAの上界という。
β∈Rが、任意のx∈Aに対し、β≦xであるとき、βをAの下界という。Aの上界（下界）が存在するとき、Aは上に有界（下に有界）であるという。Aが上に有界かつ下に下界であるとき、Aは有界であるという。
例１ 空でない実数Rの部分集合
α≧1の実数αに対して、任意のx∈Aはα≧xだから、αはAの上界で、1はAの最小の上界である。
β≦0の実数βに対して、任意のx∈Aはβ≦xだから、βはAの下界で、0はAの最大の下界である。また、Aは上に有界でかつ下に有界だから、Aは有界である。
§２ 上限と下限
空でない実数Rの部分集合Aが上に有界（下に有界）ならば、Aの上界（下界）の全体集合Bには最小数（最大数）が存在する。Aの上界の最小数をAの上限といい、sup Aあるいは
であらわす。
Aの下界の最大数をAの下界といい、inf Aあるいは
であらわす。
Aが上に有界（下に有界）でないとき、sup A=+∞、inf A=−∞とあらわす。
定理１
sup A=αである必要十分な条件は、任意のx∈Aに対してx≦α、かつ、任意の正数ε>0に対してα−ε<xを満たすx∈Aが存在することである。すなわち、
すなわち、
定理２
A⊂Bならば、inf B ≦ inf A ≦ sup A ≦ sup B【証明】
inf A ≦ sup Aは、上限・下限の定義よりあきらか。
x∈Aならばx∈Bだからx≦βとなり、矛盾する。
よって、α≦βで、sup A ≦ sup Bである。inf A=α、inf B=β、β>αとする。
x∈Aならばx∈Bだからx≧βとなり、矛盾する。
よって、β≦αで、inf B ≦ inf Aである。（証明終了）
例２
このとき、inf A = 0、sup A = 1、inf B = −1、supB = 2だから、inf B < inf A < sup A < sup Bとなり、inf B ≦ inf A ≦ sup A ≦ sup Bが成立している。
A⊂Cで、inf C=0、sup C=1だから、inf C = inf A < sup A = sup Cとなり、inf C ≦ inf A ≦ sup A ≦ sup Bが成立している。
問 開区間I=(a,b)とするとき、inf I = a、sup I=bであることを示せ。
開区間I=(a,b)は
したがって、aは集合Iの下界、bは集合Iの上界である。
inf I=α<aとする。 
したがって、inf I=aである。
sup I= β>bとする。 
したがって、sup I=bである。
（解答終了）ニュートン法 [ネコ騙し数学]
f(x)を微分可能な関数とする。
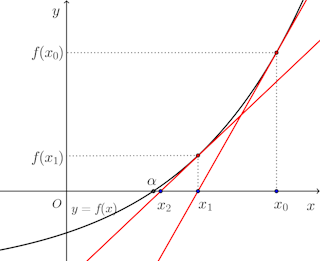
右の図のように適当な点x₁を選び、y=f(x)の点(x₁,y₁)における接線の方程式は
そして、同様に
における接線の接線を引き、この接線とx軸との交点のx座標x₃を求めると、
はf(x)=0の解、x=αに近づいてゆくことが予想される。
これがニュートン法である。
漸化式の形で書けば、ニュートン法は次のようになる。
x=√3の近似値をニュートン法を用いて求めることにする。
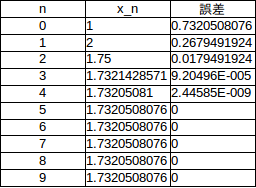
f'(x)=2xだから、
４、５回計算するだけで、x=√3≒1.732050808という近似値に到達している。
ニュートン法は前回の２分法よりも速く、しかも急速に収束することがわかると思う。
ただし、ニュートン法は、次の例のように、収束しないことがある。
接線の方程式が、それぞれ、
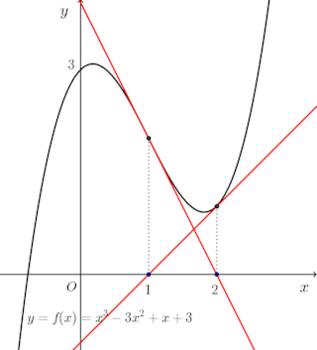
この他にも、f'(x)=0になる点に差し掛かったとき、ゼロ割が発生するなど、危険な一面も有している。
こういうことは極まれにしか起きないけれど、運悪くこのような事態に遭遇することがある。２分法と比較すると、ニュートン法は収束の速度は速いけれど、安定性に欠ける。
微分と差分 [ネコ騙し数学]
微分と差分
f(x)を何度でも微分可能な関数とする。
このとき、f(a+h)は、以下のようにテーラー展開が可能である。 
（３）、（４）式とも１次以降の項を落としているので、誤差は１次オーダ、すなわち、O(h)である。
また、（１）から（２）を引くと 
（５）式は、h²以降の項を落としているので、誤差はhの２次オーダ、O(h²)。
x軸上に等間隔hでならぶの点の集まりに正の方向に向かって整数の番号をつけると、
という点の列、点の列が得られる。
とすると、（３）、（４）、（５）式は次のように書き換えることができる。
このように書くのは面倒なので、
と略記することにすると、（３）、（４）、（５）の近似式は
このように、無限小の微分を有限な差の形で近似する方法を差分法という。
（６）を前進差分、（７）を後退差分、（８）を中心差分という。２次導関数f''(x)の近似式は、次のように求めることができる。
（１）と（２）を足すと、 
なお、（６）、（７）式は不等間隔で点がならんでいる場合でも、（６）式では
、（７）式は
とおくことによって成り立つが、（８）、（９）は不等間隔の場合、成り立たないので注意が必要。
のx=0における微分係数を（６）、（７）、（８）を使って求めてみる。
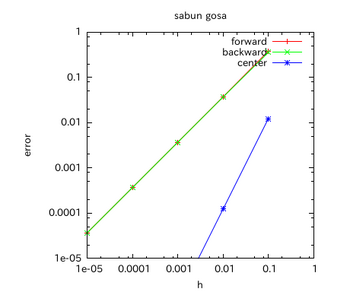x=2のときの微分係数の誤差とxの増分hとの関係を右図に示す。
このことは、前進・後退差分の誤差のオーダーが１次であり、中心差分の誤差のオーダーが２次であることを指し示しており、理論通りというわけ。
つまり、hが1/10になったとき、前進、後退差分の精度が１０倍良くなるのになるのに対して、中心差分は精度は１００倍向上する。
数値積分 台形公式、中点公式とシンプソンの公式の導出と誤差 [ネコ騙し数学]
数値積分 台形公式、中点公式とシンプソンの公式の導出と誤差
次の定積分を考える。
関数f(x)が何度でも微分可能、つまり、
級であるとき、f(a+t)は次のようにテーラー展開することが可能。
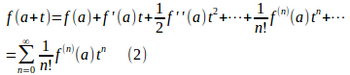
あるいは、
（２）を（１）に代入すると
したがって、
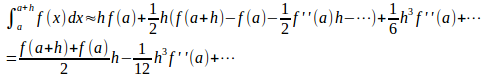
a+h=bと置けば
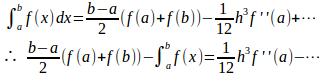
したがって、
との誤差は
程度ということになる。
そして、この結果を用いて、
より厳密な議論は、たとえば、ねこ騙し数学の次などを見て欲しい。
台形公式の精度を求める問題
積分区間[a,a+h]の中点をcとし、x=t+cという変換をすると、dx=dtで、x=aにはt=−h/2、x=a+hにはt=h/2が対応するので、
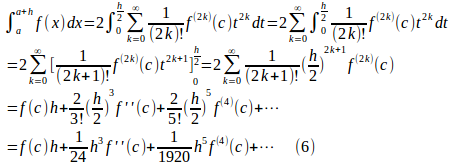
になる。
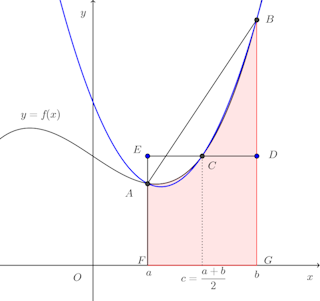a+h=bとおくと、 
上の議論から、中点公式の誤差は
[a,b]でf(x)>0のとき,
また、
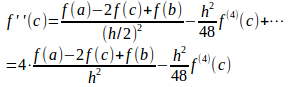
として、（６）式に代入すると、
これから、シンプソンの公式の誤差が
シンプソンの公式は
で、（８）式と
（９）式の形で（８）式を書きなおすとき、hを2hに変えれば良いので、次のようになる。
２次精度のルンゲ＝クッタ法 [ネコ騙し数学]
２次精度のルンゲ＝クッタ法
α、βを適当に選ぶと、所定の誤差の範囲で、
における定積分を
微分方程式は
ところで、
を点
でテーラー展開し、h²で打ち切ると
一方、同じくテーラー展開し、１次で打ち切ると
以上のことまとめると、
これが２次精度のルンゲ＝クッタ法と呼ばれるものであり、その導出の流れるになる。
これをコンピュータや手計算で近似計算する場合、次のようにすればよい。
２次精度のルンゲ＝クッタ法
修正オイラー法は
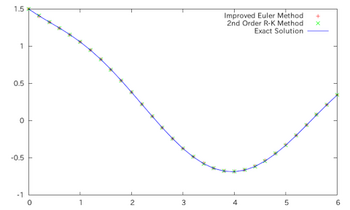２次精度のルンゲ＝クッタ法と修正オイラー法を用いて次の微分方程式を数値的に解いた結果は次の通り 
この結果から、２次精度のルンゲ＝クッタ法と修正オイラー法の精度が同程度であることが理解できると思う。
