上限・下限の問題

上限・下限の問題

問題を解く前に、最大数、最小数の定義を与える。

最大数・最小数の定義

Aを空でない実数Rの集合とする。

α∈Rが、α∈AかつAの上界であるとき、αをAの最大数といい、max Aであらわす。

β∈Rが、β∈AかつAの下界であるとき、βをAの最小数といい、min Aであらわす。

問題１

　　

とする。sup A、inf A、min A、max Aを求めよ。

【解】

sup A = 1、inf A=−1、max A = 1。

min Aは存在しない。

（解答終了）

 

問題２

Aを空でない実数Rの集合とする。

max A（min A）が存在するための必要十分条件は、Aが上に有界（下に有界）であって、かつsup A∈A（inf A∈A）であることをを示せ。

【解】

max A=αとする。αはAの上界だから任意のx∈Aに対してx≦αで、任意の正数ε>0に対してα−ε<α∈A。したがって、α=sup Aで、sup A∈Aである。

β=sup Aとすると、任意のx∈Aに対してx≦βでβ∈Aだから、β=max Aである。

min A=αとする。αはAの下界だから任意のx∈Aに対してx≦αで、任意の正数ε>0に対してα+ε>α∈A。したがって、α=inf Aで、inf A∈Aである。

β=inf Aとすると、任意のx∈Aに対してx≦βでβ∈Aだから、β=min Aである。

（解答終了）

問題３　次の集合の上限と下限を求めよ。

　　

【解】

　　

だから、t=π/nとおくと

　　

n=1のときt=π、n→∞のときt→0。

t∈(0,π]として、

　　

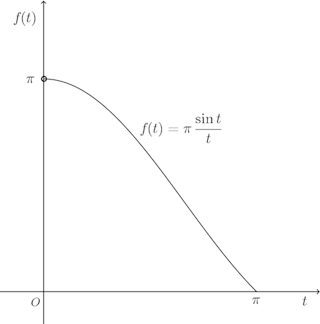とおくと、f(t)のグラフは右図になり、単調減少となる。

したがって、f(t)の上限は

　　

下限（最小数）は

　　

以上のことより、sup A =π、inf A = 0である。

（解答終了）

問題４ 空でない実数Rの部分集合Aに対して

　　

とおく。

このとき、

　　

を証明せよ。

ただし、−(−∞)=∞、−(∞)=−∞とする。

【証明】

−Aが上に有界であるとする。

α=sup (−A)とおくと、すべての−x∈−Aに対してα≧−x。したがって、すべてのx∈Aに対してx≧−αとなり、−sup(−A)=−αはAの下界になる。inf AはAの下界の最大数だから、

　　

inf A=βとすると、すべてのx∈Aに対してx≧β。したがって、すべての−x∈−Aに対して−x≦−βとなり、−inf A=−βは−Aの上界である。sup (−A)は−Aの上界の最小数だから、

　　

（１）と（２）から、

　　

−Aが上に有界でないとすると、Aは下に有界でない。

すなわち、sup (-A)=∞、inf A=−∞。

よって、

　　

である、

−(−A)=Aだから、（３）より

　　

（解答終了）

タグ：極限 微分積分