第２回 定積分の定義に基づいた計算例

第２回　定積分の定義に基づいた計算例

定積分（リーマン積分）の定義を最初に示す。

（リーマン）積分の定義

関数f(x)は有界閉区間[a,b]で有界とする。

任意の分割Δとそのそれぞれのの任意のに対して

　　

であるとき、関数f(x)は[a,b]で積分可能といい、

　　

とあらわす。

なお、ここでいう分割とは

　　

のことで、以降

　　

と略記することにする。

 

問１　定数関数f(x)=cは、任意の有界閉区間[a,b]で積分可能で

　　

であることを示せ。

【解】

分割とを任意にとると

　　

となり、分割やのとり方にかかわらない定数である。

したがって、
　　

となり、f(x)は[a,b]で積分可能で、

　　

である。

（解答終）

問２（ジャンプする関数）

関数f(x)を[a,b]で定義された関数、さらに、c>0で、a<d<bとする。

このとき、

　　

は[a,b]上で積分可能で

　　

であることを示せ。

【解】

分割とを任意にとると

　　

中のが0でないのは、最も多くて、でのときに、とした場合。

したがって、
　　

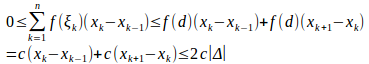
｜Δ｜→0のとき2c｜Δ｜→0だから、ハサミ打ちの定理より

　　

となり、[a,b]でf(x)は積分可能で、

　　

である。

（解答終了）

前回、x∈[0,1]で定義される次の関数

　　

が（リーマン）積分可能でないことを示したが、問２のように不連続な関数であっても積分可能な場合がある。

問３　0≧a<bとする。このとき、[a,b]上の関数f(x)=x²は[a,b]で積分可能で、

　　

となることを示せ。

【解】

分割とを任意にとると

　　

[a,b]で定義された関数g(x)=x²/3とすると、g(x)はで連続、で微分可能だから、平均値の定理より

　　

となる、が存在する。

このという特別な点を選び、このリーマン和を求めると

　　

となる。

　　

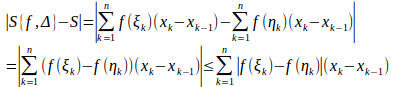
f(x)=x²はで単調増加だから

　　

また、だから、

　　

で、｜Δ｜→0のとき(b²−a²)｜Δ｜→0だから、

　　

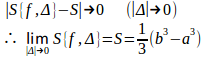
となり、 f(x)=x²は[a,b]で積分可能、そして、

　　

である。

（解答終）

タグ：定積分 微分積分