第９回 微積分の基本定理など

第９回　微積分の基本定理など

定理１２

関数f(x)が区間I上で連続であるとする。このとき、I上の関数F(x)に対して

（１）　F(x)がf(x)の不定積分である

（２）　F(x)がf(x)の原始関数である

は同値である。

【証明】

（１）⇒（２）

F(x)をf(x)の不定積分とすると、

　　

したがって、
　　

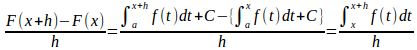
f(x)はIで連続だから、積分の平均値の定理より

　　

となるθが存在する。

したがって、

　　

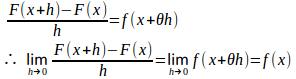
（２）⇒（１）

F(x)をf(x)の原始関数とすると、

　　

また、f(x)の不定積分

　　

とすると、

　　

よって、

　　

したがって、

　　

となり、F(x)はf(x)の不定積分である。

（証明終）

以上のことより、次の定理が成り立つ。

定理１３　（微積分の基本定理）

f(x)が区間I上で連続とする。定点a∈Iと任意のx∈Iに対し

　　

とおくと、F(x)はIで微分可能であり、

　　

である。

さらに、次の定理。

定理１４

f(x)が区間I上で不定積分をもつならば、その不定積分はI上で連続である。

【証明】

f(x)の不定積分をF(x)、a∈Iとすると、

　　

xがIの端点でないとき、x∈[x−δ,x+δ]⊂Iとなる正数δ>0を選ぶと、f(x)は[x−δ,x+δ]で有界だから、

　　

となる正の定数Mが存在する。

そこで、0<h<δとすると、

　　

−δ<h<0とすると

　　

したがって、

　　

となり、連続である。

xがIの端点であるときも同様。

（証明終）

 

定理１５

f(x)を[a,b]であるとする。F(x)がf(x)の原始関数であれば、

　　

である。

【証明】

f(x)は[a,b]で連続でF(x)はf(x)の原始関数だから、定理１２よりF(x)はf(x)の不定積分であり、

　　

と表せる。

よって、

　　

（証明終）

そして、これで、高校の定積分の公式

　　

に結びついた。

 

タグ：微分積分 定積分