微分の復習

微分の復習

 

§１　微分係数

 

定義

関数f(x)が点aの近傍で定義されていて、極限値

が存在するならば、f(x)は点aで微分可能という。このとき、この極限値

　　

をf(x)の点aにおける微分係数といい、f'(a)であらわす。

 

a+h=xとおけば、微分定数の定義式（１）は

　　

とあらわすことができる。

 

f(x)が点aで微分可能である必要十分な条件は、点aの近傍で

　　

と表せる一定の実数Aが存在することである。このとき、A=f'(a)である。

このことは、（３）式の両辺をh≠0で割ると

　　

となることから明らかだろう。

 

例１　f(x)=x²は点aで微分可能である。

　　

となるから、A=2a、ε(h)=hとおくと、

　　

したがって、f'(a)=2aである。

f(x)=x³の場合、

　　

だから、A=3a³、ε=3ah+h²とおくと

　　

したがって、f'(a)=3aである。

 

例１のf(x)=x³のε(h)を見るととわかるとおり、一般にε(h)はhのみで定まらないことに注意。

 

定理（微分可能な関数の連続性）

関数f(x)が点aで微分可能ならば、f(x)は点aで連続である。

［証明］

x≠aのとき

　　

だから、f(x)が点aで微分可能のとき

　　

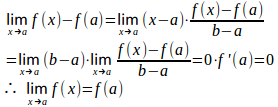
よって、f(x)が点aで微分可能ならば、f(x)は点aで連続である。

（証明終）

 

例２　関数f(x)=｜x｜はx=0で微分可能でない。

何故ならば、

h>0のとき

　　

h<0のとき

　　

となるので、

　　

は存在しないから。

つまり、上の定理の逆は成立しない。

 

上の定理の対偶をとると、「関数f(x)は点aで連続でないならば、f(x)は点aで微分可能でない」になる。つまり、f(x)は点aで不連続ならば、点aで微分不可能である。

 

例３

　　

は、x=1で不連続だから、x=1で微分不可能である。

現に、
　　

で、f'(1)は存在しない。

 

点aで微分可能でなくても、

左側微分係数

　　

右側微分係数

　　

が存在することがある。

したがって、微分可能の定義より、f(x)が点aで右側および左側微分可能であってであるとき、f(x)は点aで微分可能である。

 

 

§２　導関数

 

開区間Iで定義された関数f(x)がIのすべての点で微分可能であるとき、f(x)はIで微分可能であるといい、

　　

をf(x)の導関数という。

関数f(x)が開区間(a,b)上で微分可能でかつ点aで右側微分可能、点bで左側微分可能であるとき、f(x)は閉区間[a,b]で微分可能であるといい、

　　 

とする。

 

 

タグ：微分積分