導関数の性質 [ネコ騙し数学]
導関数の性質
導関数の定義
区間Iで定義された関数f(x)がIのすべての点で微分可能であるとき、f(x)はIで微分可能であるといい、
をf(x)の導関数という。
定理 (和・積・商の導関数)
関数f(x)、g(x)を区間Iで微分可能ならば、λf(x)+μg(x)(λ、μは実数)、f(x)g(x)はIで微分可能で
g(x)≠0のとき、f(x)/g(x)はIで微分可能で
[証明]
(1) h≠0のとき
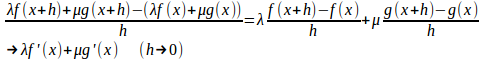
(2) h≠0のとき、仮定よりg(x)はIで微分可能だからIで連続()なので、
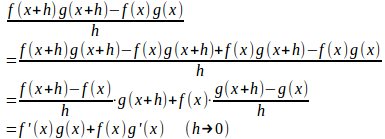
(3) h≠0でg(x)≠0のとき、
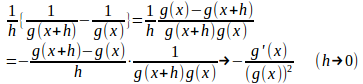
上の結果と(3)より
(証明終)
定理 (合成関数の微分)
関数y=f(x)は区間Iで微分可能、z=g(y)は区間J(f(I)⊂J)とする。このとき、合成関数はJ上で微分可能であり、
すなわち
[証明]
示すべきことは、F(x)=g(f(x))とおき、すべての点a∈Iで
b=f(a)(a∈I)とおき、y∈J上の関数φ(y)を
と定めると、g(y)はJ上で微分可能だからJ上で連続である。同様にf(x)もI上で連続だから、φ(f(x))もI上で連続で、
である。
φ(y)の定義より、点bの近傍で
だから、y=f(x)とおくと、
よって、
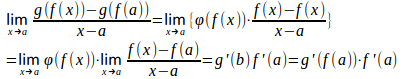
したがって、
(証明終)
x≠aのとき、f(x)=f(a)、つまり、f(x)–f(a)=0になる場合があるので、 一般に
と変形することはできない。
したがって、x≠aのとき
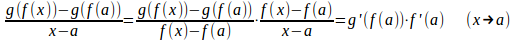
といった証明は許されない。
例えば、
g(y)=y(y∈R)としたとき、点a>0の場合を考えよ。このとき、点aの近傍ではf(x)=f(a)=0である。
点aの近傍でf(x)≠f(a)であるならば、y=f(x)、b=f(a)とおくと、x→aのとき、y→bでg(y)→g(b)となり、
![]()
したがって、
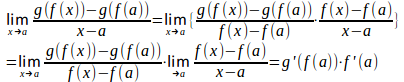
といった証明が許される。
定理 (逆関数の導関数)
関数y=f(x)は区間Iで狭義単調であるとする。f(x)がIで微分可能でつねにf'(x)≠0ならばf(I)で微分可能で
つまり、
である。
[証明]
f(x)はI上で狭義単調だから、x≠a(x,a∈I)⇔f(x)≠f(a)(f(x)、f(a)∈f(I))。
y=f(x)、b=f(a)とおくと、x≠a⇔f(x)≠f(b)だから
また、y→bのときx→aだから、
よって、f⁻¹(y)はy=bで微分可能である。
(証明終)
定理 (媒介変数・パラメータで表された関数の導関数)
x=f(t)、y=g(t)は区間Iで微分可能でf'(t)≠0とする。x=f(t)に逆関数が存在すれば、
である。
[証明]
仮定より、x=f(t)には、逆関数t=f⁻¹(x)が存在して微分可能。したがって、となり、
合成関数と逆関数の微分より
(証明終)
分数同士のの掛け算のように
と考えるとわかりやすい。



