テーラーの定理とテーラー展開、マクローリン展開 [ネコ騙し数学]
第10回 テーラーの定理とテーラー展開、マクローリン展開
定理 テーラーの定理
関数f(x)は閉区間[a,b]でn−1回連続微分可能、開区間(a,b)でn回微分可能ならば
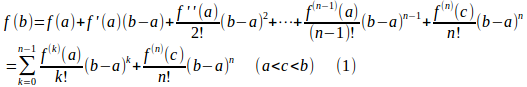
となるcが少なくとも1つ存在する。
[証明]
![]()
となるようにKを定め、
とおくと、F(a)=F(b)となる。
F(x)は[a,b]で連続、(a,b)で微分可能であり、F(a)=F(b)だからロールの定理よりF'(c)=0 となるcがa<c<bに少なくとも1つ存在する。
F(x)を微分すると、
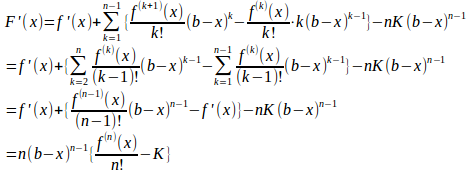
したがって、
(証明終了)
n=1とすると、平均値の定理が得られる。
極値の判定などで重要なn=2のときは以下のようになる。
b=x、と置き、(1)式を書き直すと
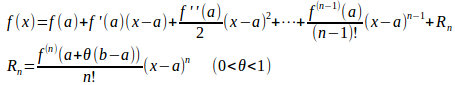
となり、をLagrange(ラグランジュ)の剰余項という。
fが級ならばすべての非負の正数nについて(1)は成り立ち、
である点xでは
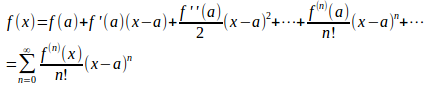
となり、この級数をx=aまわりのテーラー級数という。
特に、a=0のときに得られるx=0まわりのテーラー級数
![]()
をマクローリン級数という。
以下に代表的なマクローリン級数を示す。
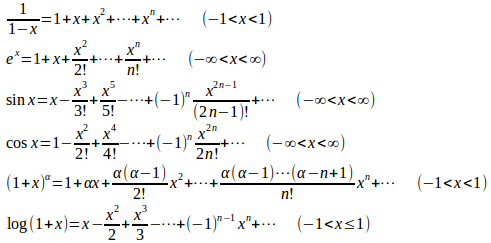
関数f(x)が
とべき関数の級数として展開されるとき、これはテーラー展開(マクローリン展開)に他ならない(テーラー展開の一意性)ことが知られている。
だから、
にx=–tを代入すると、
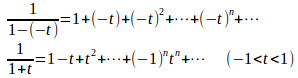
になるので、のマクローリン級数を
と求めることができる。
同様に、
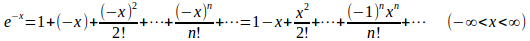
と、のマクローリン級数を利用して
のマクローリン級数を簡単に求めることができる。



