凸関数の問題２ [ネコ騙し数学]
凸関数の問題２
問題を解く前に、関数の凹凸の定義を再掲する。
区間Iで定義された関数f(x)が、Iの任意の点x₁、x₂（x₁<x₂）に対して、x₁<x<x₂ ならば
であるとき、f(x)を凸関数という。また、このとき、f(x)は下に凸という。
また、 –f(x)が凸関数であるとき、f(x)を凹関数という。
とおくと、（１）式は
と変形できる。
したがって、凸関数の定義に、（１）、（２）式のどちらを使用してもよい。
また、1–t =α、t=βとおくと、（２）式は
となるので、（３）式を凸関数の定義に使用してもよい。
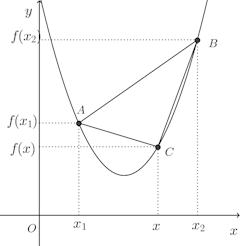
また、f(x)が凸関数のとき、
が成立し、
直線AC勾配≦直線ABの勾配≦直線CBの勾配
である。
さらに、次の定理をあらためて紹介する。
定理 （凸関数と２次導関数）
関数f(x)が区間Iで連続、区間Iの内部で２回微分可能とする。f(x)がIで凸関数である必要十分な条件は、Iの内部でf''(x)>0であることである。
問題１ 次の問に答えよ。
（１） 開区間Iでf(x)>0、f(x)は２回微分可能とする。このとき、logf(x)が凸関数ならばf(x)が凸関数であることを証明せよ。
（２） 区間でf(x)>0とする。logf(x)が凸関数ならばf(x)は凸関数であることを証明せよ。一般に逆は成立しない。
［解］
（１） logf(x)はIで２回微分可能。
問題の条件よりlogf(x)は凸関数だから、定理より
。
よって、
したがって、logf(x)が凸関数であるとき、f(x)は凸関数である。
（２） x、yを区間Iの任意の点とし、0<t<1とする。
logxは増加関数だから、
logf(x)がで凸関数ならばf(x)も凸関数になる。
（解答終）
（※） a>0、b>0、0<t<1のとき
である。
問題２ fは区間Iで定義された凸関数とする。このとき、次のことを証明せよ。
（１） 任意のx∈Iに対して
は増加関数である。
（２） Iが開区間であるとき、fは任意の点x∈Iで右側微分および左側微分が可能である。
（３） Iが開区間であるとき、fは連続である。
［解］
（１） 凸関数の定義より明らか（右上のグラフ参照）。
（２） x₁<x<x₂とする。
xとx₂を固定し、x₁を増加させると、（１）より
は増加する。また、
だからは上に有界である。したがって、x₁→x-0のとき極限値
が存在する。すなわち、
であり、点xで左側微分可能である。
xとx_1を固定しx₂を減少させると、（１）より
は減少し、
だから、は上に有界。したがって、
が存在し、点xで右側微分可能である。
（３） Iが開区間のとき、（２）より、任意のx∈Iでfは右側、左側微分が可能である。したがって、fは点xで左側連続、右側連続。したがって、fは点xで連続である。
（解答終了）
（３）を式で書くと
そして、問題２は次の定理の証明になっている。
定理 関数fが閉区間[a,b]で凸関数ならば、fは開区間(a,b)で連続である。
