ロピタルの定理の怪３

ロピタルの定理の怪３

 

定理A

f(x)、g(x)は点aを除く点aの近傍で微分可能でg'(x)≠0である。このとき、

　　

で、かつ、が存在するならば、が存在し、

　　

である。

 

定理B

f(x)、g(x)は点aを除く点aの近傍で微分可能でg'(x)≠0である。このとき、

　　

で、かつ、が存在するならば、が存在し、

　　

である。

 

定理Aを元にして定理Bを証明（？）してみようではないかというお話。

 

【定理Bの証明（？）】

だから

　　

しかもだからaの十分近くではf(x)>0、g(x)>0で、f(x)≠0、g(x)≠0である。したがって、1/f(x)、1/g(x)は、aの十分近く（x≠a)で微分可能。

よって、ロピタルの定理Aより

　　

である。

ここで、

　　

これを⑨式に代入すると、

　　

 

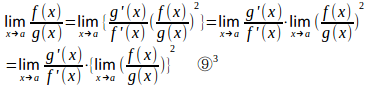
⑨³より、のとき

　　

 

のとき、

　　

だから、上と同様に考えて

　　

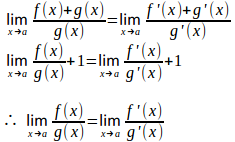
（Q.E.D.）

 

この証明が正しければ、難しいε-δ論法を使わない優れた証明です(^^)

 

数学の教科書の中には、

∞/∞の極限は、

だから、φ(x)=1/f(x)、ψ(x)=g(x)とおくと

と、0/0の極限に帰着させることができ、定理Aから云々

といった趣旨のことが書かれているものがあるとかないとか。

おそらく、上の証明（？）は、こうした方針のもとでなされたものなのでしょう。

そして、この方針にしたがって次の問題を解こうとすると大変なことになる(^^)

 

問題　次の極限を求めよ。

　　

【解】

これは∞/∞の極限だから

　　

(・・?

確かに、

　　

ではあるが、問題をより複雑化させている(^^)

 

それにしてもロピタルの定理は恐ろしい。そして、ロピタルの定理（使用）の闇は未だ深い！！