微分の問題・・・の続き

前回の話の続き！！

 

前回、関数f''(x)が点aの近傍(a–r,a+r)（r>0） でC²級であれば、

　　

であるということを示した。

では、

　　

と、f(x)の２次微分係数f''(a)を（１）式の右辺で近似したときの誤差はどの程度だろうか？

 

fが級であるとき、O形式のテーラーの定理は

　　

である。

n=2とすると、

　　

になる。

これを（１）式に代入すると、

　　

だから、（１）の近似式の誤差はh程度と予測できる。

 

だが、近似式（１）の誤差h程度ではない。このことは、、a=1とし、h=0.1、h=0.01の場合で計算すると、このことはすぐに確かめられる。

実際、h=0.1のときの誤差は0.00226599、h=0.01のときの誤差は0.000022652で約1/100になっている。つまり、hを1/10にすると、誤差は約1/100になっており、誤差はh²に比例していることになる。つまり、（１）式の近似式の誤差はO(h²)である。

 

なぜ、このようなことが起きたかというと、n=3としてf(a+h)をテーラー展開すると、この理由がわかる。

　　

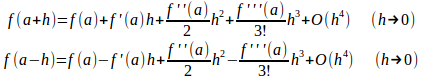
奇数次の項の符号がf(a+h)とf(a–h )では正負が異っており、f(a+h)とf(a–h )を足し合わせると、奇数次の項が消えてしまうのだ。だから、誤差はO(h)ではなく、O(h²)になってしまう。実際、これを（１）式の右辺に代入すると、

　　

となることからも確かめられる。

矛盾しているといえば矛盾していないし、矛盾していないといえば矛盾していないような気がする(^^ゞ

 

実は、これと同じような奇妙なことが次の極限を求めるときに発生する。

　　

（２）、（３）式から、x→0のとき、sinxは、xと同位の無限小でO(x)で、かつ、O(x³)であるということになる。ランダウの記号、関数の無限小の定義からそうなると言われればそれまでなのだが、考えてみれば、これも奇妙な話のように思えてならない。どうやら、微分積分や解析学、そして、数値計算などでよく使用されるランダウの記号は正体不明の、かなり胡散臭いシロモノ、バケモノなのかもしれない。

何しろ、ランダウ記号（ビッグ・オーO）の計算規則は、

　　

で、普通の算法は通用しないのだから。

したがって、これを使うときには細心の注意が必要に違いない。

 

さて、ランダウ記号の計算規則⑨が成立する例として、

　　

としたときの誤差を調べてみることにする。

　　

だから、

　　

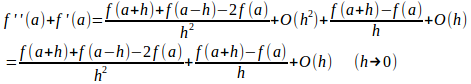
になるはずである。

、a=1として、hを変化させて、絶対誤差
　　

を計算してみると、次のグラフのような結果になる（赤線）。

比較参照のために、

を用いて、f''(a)+f'(a)を計算した値もグラフ中に示してある（緑線）。

グラフの縦軸には近似値との誤差の絶対値を、横軸にはhをとり、対数グラフで計算結果を示してある。

赤の直線（？）の勾配が約１で誤差がh程度、緑の直線の勾配が約２でh²程度であることから、近似式⑨³の誤差がO(h)であること、そして、計算規則⑨の妥当性が確かめられると思う。