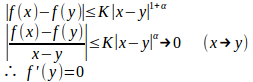リプシッツ連続と一様連続

第１９回　リプシッツ連続と一様連続

 

Xを実数Rの空でない部分集合とし、fをXからRへの関数とする。このとき、任意のx₁、x₂∈Xに対して、あるK≧0が存在し、

　　

であるとき、fはXでリプシッツ連続という。また、（１）式の定数Kをリプシッツ定数と呼ぶ。

 

関数f(x)がXでリプシッツ連続であるとき、f(x)がXで連続であることは、次のように証明できる。

 

すべてのx₁、x₂∈Xとする。

K=0のとき、（１）式より、

　　

となり、f(x)は定数関数。よって、Xの各点で連続である。

K>0のとき、x₁を固定し、任意の正数に対して、δを

　　

をとれば、

　　

になるので、f(x)はすべてのx₁∈Rで連続である。

また、このことから、関数f(x)がリプシッツ連続であれば一様連続であることがただちにわかる。

 

一様連続

fを区間Iで定義された関数とする。任意のε>0に対し、次の条件を満たすδ>0が存在するとき、fはIで一様連続であるという。

　　

 

一様連続の定義から、関数f(x)が区間Iで一様連続であればIで連続であることは明らか。そして、リプシッツ連続であれば一様連続であるので、次のような関係がある。

　リプシッツ連続⇒一様連続⇒連続

一般に、逆は成立しない。

 

一様連続に関しては、重要な次の定理があるが、証明なしで定理だけを紹介しておく。

 

定理

関数fが有界閉区間Iで連続ならば、fはIで一様連続である。

 

上のは、有界閉区間でなければ、一般には成立しない。

 

例１　f(x)=x²（0≦x<∞）は一様連続でない。

とおき、δ=1/nとする。

　　

このとき、

　　　

このようなx₁、x₂を取った場合、nを大きくし、δ>0を限りなく小さくして0に近づけても、1より小さくなることはない。よって、f(x)は[0,∞)で一様連続ではない。

 

（注）

一様連続の定義は

　　

したがって、一様連続でないは、上の否定

　　

例１ではこれを使用している。

 

これを数学で使われる翻訳調日本語に訳すと、

一様連続でないとは、

あるε>0が存在し、任意のδ>0に対して、あるx₁、x₂∈Iが存在し、

　　

を満たすことである

とか(^^ゞ

 

また、次のように、区間Iが有界閉区間でなく、有界な開区間であっても、Iで連続な関数な関数がIで一様連続になることがある。

 

例２　f(x)=x²（x∈(0,1))は区間(0,1)で一様連続である。

任意のx₁、x₂∈(0,1)とする。

　　

したがって、f(x)は(0,1)でリプシッツ連続であり、一様連続である。

あるいは、任意のε>0に対して、δ=ε/2>0をとると、

　　

よって、一様連続である。

 

次の例３のように、有界な区間でなくても、リプシッツ連続であり、一様連続になる場合もある。

 

例３　f(x)=sinx （x∈(−∞,∞）） は（−∞,∞）でリプシッツ連続であり、一様連続である。

任意のx₁、x₂∈(−∞、∞）とする。

　　

したがって、sinxは、(−∞,∞)でリプシッツ連続であり、一様連続である。

あるいは、任意のε>0に対して、δ=ε>0をとると、

　　

よって、一様連続である。

 

 

問１　平均値の定理を使って、

　　

が成り立つことを証明せよ。

 

問２　f(x)=logx （x≧1）は[1,∞)で一様連続か。

【解】

x₁、x₂∈[1,∞)とし、x₁≠x₂とすると、平均値の定理より

　　

となるcがx₁とx₂の間になる。

したがって、c>1となり、

　　

よって、任意の正数ε>0に対して、

　　

とδを定めれば、

任意のε>0に対して、

　　

よって、[1,∞)で一様連続である。

（解答終）

 

 

余力のあるヒトは、「f(x)=√x （x∈[0,∞)）は[0,∞)で一様連続か」にチャレンジしてみるといいだろう。

 

 

問題　区間Iで微分可能な関数f(x)が、任意のx、y∈Iに対して

　　

を満たせば、関数f(x)は定数である。

【解】

任意のx、y∈I（x≠y）とする。

　　

したがって、fはIで定数である。

（解答終）