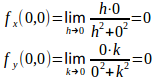第0回 方向微分と偏微分、そして、全微分 [ネコ騙し数学]
第0回 方向微分と偏微分、そして、全微分
§1 方向微分と偏微分
fをR²の部分集合DからRへの写像(関数)とし、さらに、u=(h,k)とする。
tを変化させたとき、
の平均変化率は
をとり、t→0の時の(1)式の極限
を考えると、これはベクトルu=(h,k)に沿っての変化率で、u=(h,k)に沿っての方向微分係数という。これを記号で表す。すなわち、
である。
特に、u=e₁=(1,0)としたときの、e₁=(1,0)に沿っての方向微分係数
は、yをbに固定してxだけを変化させたときの変化率であり、関数fの点(a,b)でのxに関する偏微分係数といい、記号、などで表す。それ故、次のように表すことができる。
u=e₂=(0,1)としたときの、e₂=(0,1)に沿っての方向微分係数
は、xをaに固定してyだけを変化させたときの変化率であり、関数fの点(a,b)でのyに関する偏微分係数といい、記号、、
などで表す。同様に、
問1 次の関数の点(0,0)における、xとyの偏微分係数を求めよ。
【解】
(解答終)
1変数関数f(x)は、x=aにおける微分係数f'(a)が存在するならばx=aで連続であるが、2変数関数f(x,y)の場合、点(a,b)の偏微分係数が存在してもf(x,y)が点(a,b)で連続である保証はない。
たとえば、問1の関数f(x,y)は点(0,0)で連続でない。
§2 全微分
関数f(x)が点x=aで微分可能である必要十分条件は、
である。ここで、A=f'(a)であり、o(h)はランダウ記号(ランダウのスモール・オー)、すなわち、
である。
(8)式を2変数関数f(x,y)に拡張すると、
になるであろう。ここで、A、Bはh、kに無関係な定数であり、
である。
この関係式(9)が成り立つとき、2変数関数f(x,y)は点(a,b)で全微分可能、あるいは、微分可能であるという。
f(x,y)が全微分可能であるとき、(9)式より、
![]()
となり、f(x,y)は点(a,b)で連続である。
定理
f(x,y)が点(a,b)で全微分可能ならば、f(x,y)は点(a,b)で連続である。
また、k=0とすると、(9)式は
となり、両辺をhで割りh→0の極限を求めると、
である。
同様に、k=0とすると、
よって、(9)式は
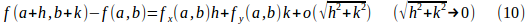
になる。
定理
f(x,y)が点(a,b)で全微分可能ならば、点(a,b)で偏微分可能で、
である。
次に、h、kを定数とし、th、tkを(10)式のh、kと見なすと、(10)式は
となり、両辺をt≠0で割り、t→0の極限をとると、
![]()
これは、u=(h,k)に沿っての方向微分係数であるから、2変数関数f(x,y)が点(a,b)で全微分可能ならば、点(a,b)で任意のu=(h,k)に沿っての方向微分係数をもち、
が成り立つ。
以上のことから、f(x,y)が点(a,b)で(全)微分可能ならば方向微分可能であり偏微分可能である。