第１回 ユークリッド空間の開集合、閉集合、境界

第１回　ユークリッド空間の開集合、閉集合、境界

 

２次元ユークリッド空間の点P(x₁,y₁)、Q(x₂,y₂)の距離を

　　

と定義する。

このとき、距離には次の性質がある。

　　

 

定義
ε>0と座標平面上の点a=(x₀,y₀)∈R²に対して

　　

を点aのε近傍という。

開集合と閉集合

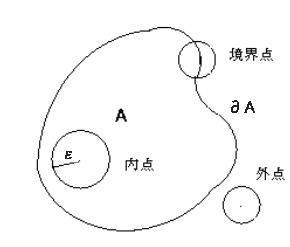
Aをの部分集合とする。

点a∈Aに対して、

　　
となるε>0が存在するとき、aをAの内点という。Aの内点の全ての集合をAの内部といい、記号やで表す。また、の点はAの内点だから

　　

である。

R²の点aについて

　　

となるε>0が存在するとき、aをAの外点という。Aの外点全体の集合をAの外部といい、記号と表す。A

R²の点aがAの内点でも外点でもないとき、aをAの境界点という。Aの境界点全体の集合

　　

をAの境界といい、∂Aで表す。

したがって、R²の点が境界点であるとは、任意のε>0に対して
　　

が成り立つことである。

定義から

　　

が成り立つ。

R²の点aについて、任意の正数ε>0に対しても

　　

が成り立つとき、をAの触点という。Aの触点全体の集合を閉包といい、やで表す。集合Aの点はAの触点だから、

　　

である。また、定義から明らかなように

　　

である。

 

R²の部分集合Aについて、が成り立つときAを閉集合といい、が成り立つとき閉集合という。

定理１　２次元ユークリッド空間R²において、開集合の補集合は閉集合、閉集合の補集合は開集合である。

 

 

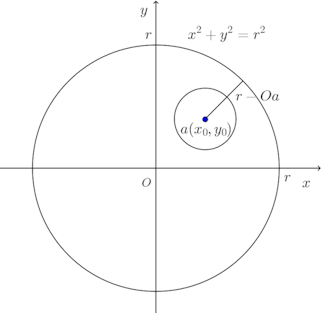
例

　　

は開集合である。

【解】

点aを集合Aの任意の点とする。

にとり、とする。

三角不等式から

　　

よって、

　　

したがって、Aは開集合である。

（解答終）

 

あるいは、

【別解】

集合Aの任意の点aの座標を(x₀,y₀)とすると、

　　

そこで、

　　

にとると、

である。

（解答終）