第３回 ２変数関数の極限

第３回　２変数関数の極限

 

記号の混乱を避けるために、２次元ユークリッド空間R²の点をアルファベットの太字の斜体字を用いてaなどであらわし、２点a(x₁,y₁)、b(x₂,y₂)の２点間の距離を

　　

と表記することにする。

 

実関数と定義域、値域の定義

Aをn次元ユークリッド空間の部分集合、fをAから実数Rへの写像とする。このとき、Aをfの定義域といい、

　　

をfの値域という。

 

n=2のとき、関数f(x,y)の定義域をAとすると、f(x,y)の値域は

　　

である。

 

 

２変数関数の極限の定義

f(x,y)は点a(a,b)の近傍で定義される関数とする。

ある実数lが存在し、任意の正数ε>0に対して、あるδ>0が存在し、

　　

である全ての点x(x,y)について

　　

となるとき、f(x,y)は点aで収束するといい、

　　

または、

　　

などと表す。

 

問１　次のことを示せ。

　　

［解］

任意の正数ε>0に対して、δ=εとδ>0を定めると、の任意の(x,y)について

　　

となるので、

　　

である。

（解答終）

 

問２　次のことを示せ。

［解］

任意のε>0に対してδ=ε/2とδ>0を定めると、の任意の(x,y)について

　　

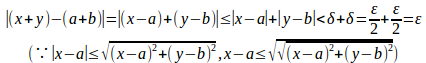
となるので、

　　

である。

 

定理２

、αとβを実数の定数とする。このとき、次が成り立つ、

　　

［証明］

基本的に１変数関数の極限の証明と同じで、1変数関数の証明中のx、aをx、a、さらに、をと変更すれば、そのまま証明が流用できます(^^ゞ

だから、（１）と（４）だけ証明することにする。

 

また、証明を簡略化するために、(x,y)をx、(a,b)をa、f(x,y)をf(x)で表すことにする。

 

（１）　α=0、β=0のときは明らかだから、αとβが同時に0でないとする。

だから、任意のに対して、

　　

となるδ₁>0、δ₂>0が存在する。

そこでδ>0をδ=min｛δ₁、δ₂｝にとると、

　　

 

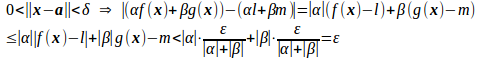
（４）　だから、任意のε>0に対して、あるδ>0が存在して

　　

よって、

　　

（証明終）

 

１変数関数のときと基本的に証明は同じなので、次の定理は定理だけを紹介する。

 

定理３

点(a,b)を除く、点(a,b)の近傍においてf(x,y)≦g(x,y)ならば