第7回 全微分 [ネコ騙し数学]
第7回 全微分
関数f(x,y)が点(a,b)の近傍で、ある定数α、βによって
と表されるとき、fは点(a,b)で全微分可能(微分可能)であるという。ここで、
である。
f(x,y)が点(a,b)で全微分可能なとき、(h,k)≠(0,0)とすると、(1)式より
となるので、f(x,y)は点(a,b)で連続である。
また、k=0のときρ=|h|となり、
同様に、h=0のとき、ρ=|k|となり、
以上のことから、次の定理が得られる。
定理8
関数f(x,y)が点(a,b)で(全)微分可能ならば、f(x,y)は点(a,b)で連続であり、かつ偏微分可能で、
である。
また、h=ρcosθ、k=rsinθとおくと、
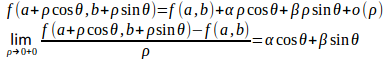
となり、この極限値をθ方向に沿っての方向微分係数という。
定義
領域Dで定義されている関数f(x,y)がD上のすべての点で(全)微分可能なとき、f(x,y)はD上で(全)微分可能であるといい、
をf(x,y)の全微分という。
dx=Δx、dy=Δyだから、(2)式は
と書くこともできる。
定義 (曲面z=f(x,y)の接平面)
関数f(x,y)は点(a,b)で(全)微分可能とする。このとき、平面
を曲面z=f(x,y)の点((a,b),f(a,b))における接平面という。
問 曲線
上の点((a,b),f(a,b))における接平面の方程式を求めよ。
【解】
よって、
とおくと、
である。
(解答終)
原点を中心とする半径rの球面と球面上の点(a,b,c)で接する平面の方程式は、
だから、問で求めた接平面の方程式と一致していることがわかると思う。
定理9
関数f(x,y)がC¹級ならば、f(x,y)は全微分可能である。
【証明】
と置くと、平均値の定理より
は連続だから、
とおくと、h→0、k→0のときε₁→0。
同様に、は連続だから、
とおくと、k→0のときε₂→0。
ゆえに、
![]()
とおくと、|h|≦ρ、|k|≦ρだから、
(証明終)
問題 関数は(0,0)で偏微分可能であるが、全微分可能でないことを示せ。
【解】
だから、(0,0)で偏微分可能である。
このとき、が0に収束すれば全微分可能で、しなければ全微分不可能である。そこで、h=t、k=tとして、t→0の極限を求めると、
よって、全微分可能でない。
(解答終了)








