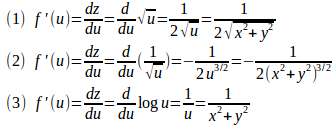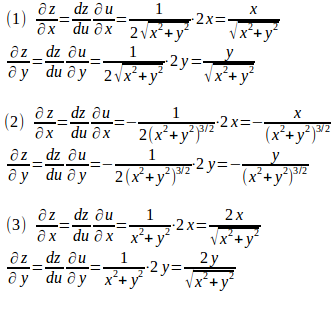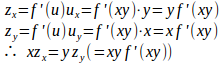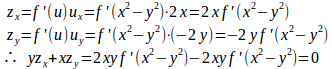第１０回 合成関数の微分法１ [ネコ騙し数学]
第１０回 合成関数の微分法１
定理１１
関数f(u)が区間Iで微分可能、関数g(x,y)が領域Dで偏微分可能かつ
ならば、合成関数F(x,y)=f(g(x,y))はDで偏微分可能で
である。
【証明】
変数yを固定すると、g(x,y)はxのだけの一変数関数φ(x)と考えることができる。
１変数関数の合成関数の微分法より
ところで、
よって、
yに関する偏微分の場合も同様。
（証明終了）
上の定理は、u=g(x,y)、z=f(u)とし、この合成関数z=f(g(x,y))の偏微分を
としたほうが、計算するときにも間違えることはないだろう。
問１ 次の関数の偏導関数を求めよ。
【解】
u=x²+y²とおくと、（１）、（２）、（３）の関数は
と書き換えられる。
z = f(u)とおき、uで微分すると
u=x²+y²の偏導関数は
だから、
（解答終了）
問２ 次の関係式が成り立つことを示せ。
（１） z=f(ax+by)のとき、
（２） z=f(xy)のとき
（３） z=f(x²–y²)のとき
（４） 
のとき
【解】
（１） u=ax+byとおくと、z=f(ax+by)=f(u)。
また、
。
よって、
（２） u=xyとおくと、z=f(xy)=f(u)。
また、
。
（３） u=x²–y²とおくと、z=f(x²–y²)=f(u)。
また、
だから、
（４） u=y/xとおくと、z=f(y/x)=f(u)。
また、
だから、
（解答終）
問３ z=f(x–ct)+g(x+ct)（cは定数）のとき、
であることを示せ。
【解】
u=x–ct 、v=x+ctとおくと、z=f(u)+g(v)。
また、
だから、
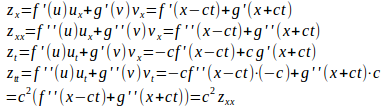
よって、
である。
（解答終了）
は波動方程式と呼ばれるもので、z=f(x–ct)+g(x+ct)はその解である。
ネムネコ、シンプレクティック法を使って微分方程式の数値積分をする！！ [ネコ騙し数学]
かつてのネムネコ・ファミリー――某Q&Aサイト上のみでネムネコと深い交流のあったヒトたち――であるddt³さんから、シンプレクティック（Symplectic）法と呼ばれる数値計算法、微分方程式の数値積分法を教えてもらったので、バタバタとプログラムを作って計算してみた。
数値計算につかったモデルは、調和振動子
で、微分方程式は
で、t=0のときの初期条件を(q,p)=(1,0)として、１次精度のオイラー法と１次精度のシンプレクティック法を使って、この微分方程式を解いてみた。
進めるタイムステップΔt=0.1として数値的に解いた。
（１）式のHはハミルトニアンと呼ばれるもので、この場合、運動エネルギーp²/2とバネの位置エネルギーq²/2の和になる。力学的エネルギーが一定だから、（２）を数値的に解いた(q,p)をプロットすると、本来、数値解は
の円周上に存在しなければならない。
しかし、１次精度のオイラー法を用いて解いた数値解は時間の経過とともにp²+q²=1の円から離れていくんだケロよ。つまり、エネルギー保存則が満たされていない！！
軌道からどんどん離れてゆくから、時間の経過とともにエネルギーが増えていく！！
１次精度のオイラー法を用いた数値計算結果
これに対し、シンプレクティック法は、多少振動するけれど、力学的なエネルギーが保存されるんだケロ。
１次精度のシンプレクティック法を用いた計算結果
数値積分法は、
１次精度のオイラー法だと
１次精度のシンプレクティック法だと
だけの差なのだけれど、この僅かな差でこれほど計算結果が異なるというのは正直驚きだにゃ。
