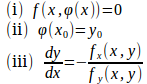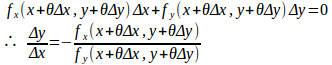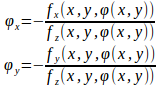ラッセルのパラドックス [ネコ騙し数学]
ラッセルのパラドックス
問題
は集合でないことを示せ。
【解】
を集合と仮定する。
A∈Aとすると、A∉Aになって矛盾する。
A∉Aでないとすると、集合の条件A∉Aをみたすので、A∈Aとなって矛盾する。
つまり、
だケロ。
これは、を集合と仮定したから、このような矛盾が生じた。
したがって、
は集合ではない。
(解答終)
を集合と認めると、ラッセルのパラドックスになってしまう。
このパラドックス回避のためには、こんなものを集合と認めちゃ〜いけねえ。認めなければ、パラドックスにはならない。
つ・ま・り、
何でもかんでも、ものの集まりを集合としちゃ〜いけねぇ
というわけ。
関数f(x)=√xが一様連続であることの証明 [ネコ騙し数学]
関数f(x)=√xが一様連続であることの証明
一様連続の定義
関数f(x)は区間Iで定義されている関数とする。任意のε>0に対して次の条件をみたすδ>0が存在するとき、f(x)はIで一様連続という。
関数の一様連続に関して、次の重要な定理に次のものがある。
定理
関数f(x)が有界閉区間Iで連続ならば、f(x)はIで一様連続である。
上の定理ではIが有界な閉区間であることが重要。
例 で定義されるf(x)=1/xは、Iで連続であるけれど、Iで一様連続ではない。
x₁、x₂∈(0,1]であるx₁、x₂を
にとると、
となり、nをどんなに小さくしても、これは1より小さくならないので、一様連続ではない。
I=[1,∞)にすると、
![]()
そこで、任意のε>0に対して、δ=εにδ>0をとると、
したがって、f(x)=1/xは区間[1,∞)で一様連続になる。
上の例のように、区間Iが有界な閉区間でなくても、Iで一様連続である関数は存在する。
問1 次の関数が一様連続であることを示せ。
【解】
平均値の定理より
となるcがx₁とx₂の間に存在する。
(1)より
任意のε>0に対して、δをδ=εにとると、
よって、一様連続である。
(解答終)
【別解】
![]()
よって、任意のε>0にたいしてδ=εとすれば、
(別解終)
問2 とする。f(x)が区間(1,∞)で一様連続であることを証明せよ。
【解】
x₁、x₂∈(1,∞)とする。
平均値の定理より
となるcがx₁とx₂の間に存在する。したがって、c>1。
よって、
そこで、任意のε>0に対して、δをδ=2εにとると、
したがって、√xは区間(1,∞)で一様連続である。
(解答終)
問3 平均値の定理を使わず、有理化を行うことで、問2を証明せよ。
問4 とする。関数f(x)は区間[0,1]で一様連続であることを証明せよ。
【解】
f(x)=√xは有界閉区間[0,1]で連続。したがって、定理よりf(x)=√xは[0,1]で一様連続である。
(解答終)
問2、問4より、は[0,∞)で一様連続ということになる。
問4は、技を使わないと、ちょっと証明しづらいので、定理を使って証明した。
そして、その技を使うと、ダイレクトには[0,∞)で一様連続であることを証明できる。
【証明】
a≧0、ε>0に対して
である。
x₁、x₂∈[0,∞)とする。
任意のε>0に対してδ=ε²とおくと
x₁≧x₂のとき
だから、
x₁<x₂のとき同様に
①と②より
したがって、任意のε>0に対して、δ=ε²とすると、
よって、f(x)=√xは[0,∞)で一様連続である。
(証明終)
ラグランジュの未定乗数法を使って大学入試の有名問題を解く [ネコ騙し数学]
大学入試の問題で非常に有名な問題がある。
問題 正の実数a、b、cがa+b+c=1を満たすとき、次の問に答えよ。
(1) abcの最大値を求めよ。
(2) であることを示せ。
(3) の最小値を求めよ。
【解】
(1) 相乗平均≦相加平均より
よって、a=b=c=1/3のときabdの最大値は1/27
(2)
(3)
相加平均≧相乗平均より
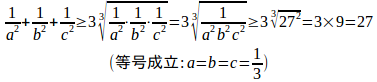
また、(2)よりだから、
![]()
したがって、a=b=c=1/3のときに最小値100/3。
(解答終了)
(2)は、シュワルツの不等式
を知っていれば、x=y=z=1とおき、
となることから、このことは容易に想像がつくが・・・。
(a,b,c)を原点を中心とする半径rの球の球面上x²+y²+z²=r²の点と考えると、
この球と平面x+y+z=1が共有点をもつ条件は、球の半径r≧平面x+y+z=1と原点との距離
と解くこともできる。
等号が成立するのは、球x²+y²+z²=r²と平面x+y+z=1が接するとき。
(3)は、相加平均≧相乗平均だから
よって、
![]()
したがって、最小値は12としてはいけない。最小値が12になるのはa=b=c=1のときだから、a+b+c=3≠1となり、問題の条件を満たさないからだ。
ラグランジュの未定乗数法を使うならば、次のように解くことができるだろう。
(1)は、 f(a,b,c)=abc、g(a,b,c)=a+b+c–1=0とし、
とすると、
a≠0、b≠0、c≠0だから、abcで割ると
また、a+b+c=1だから、a=b=c=1/3。
したがって、f(a,b,c)=abcの極値は
(2)は、f(a,b,c)=a²+b²+c²とし、
とすると、
これとa+b+c=1より、a=b=c=1/3となり、f(a,b,c)の極値は
(3)は、とおき、
とすると、
よって、
何故ならば、a>0、b>0のとき
だから。
同様に、b=c。
よって、a=b=c=1/3。
したがって、f(a,b,c)の極値は
厳密なことを言うと、ラグランジュの未定乗数法を用いるとき、(1)、(2)、(3)のいずれの場合も、a=b=c=1/3のときにf(a,b,c)が極値であることを証明しないといけない。何故ならば、(a,b,c)=(1/3,1/3,1/3)は、あくまでf(a,b,c)が極値をもつ候補の点に過ぎず、この点で極値をとる保証がないから。そして、この証明はそれほど簡単なものではない。
反転の問題 [ネコ騙し数学]
反転の問題
数学の問題集を見ていたら、反転に関する次の問題があった。
問題
原点を中心とする半径rの円の円外の点P(x,y)から接線を引き、2つの接線を結ぶ直線とOPとの交点をQ(X,Y)とするとき、PをQに写す写像を反転という。
(1) OP・OQ=r²を証明し、次の等式を導け。
(2) この反転の逆写像も反転であることを証明せよ。
(3) Pが直線x+y=1上を動くとき、Qのえがく図形の方程式を求めよ。
【解】
 (1) 円外の点Pから円に引いた接線の交点をA、Bとし△OQAと△OAPに注目する。
(1) 円外の点Pから円に引いた接線の交点をA、Bとし△OQAと△OAPに注目する。
∠AOQ=∠POA
∠OQA=∠OAP=∠R
∴ △OAQ=△OPA
よって、
①の両辺をOQ²で割ると
点Pは線分OQの延長線上にああるから、
よって、
である。
(2) ①の右辺、左辺をOP²で割ると、
よって、この反転の逆写像も反転である。
(3) x+y=1にを代入すると、
よって、点(r²/2、r²/2)を中心とする半径r²/√2の、原点Oを通る円である。
(解答終)
一般に、反転によって原点を通らない直線は原点を通る円に写され、原点を通る円は原点を通らない直線に写される。
③式に②式を代入するとx+y=1に戻るので、これから、反転によって原点を通らない円が原点を通らない直線に写ることが確かめられる。
この問題で使われている反転の定義が面白いと思ったので、今回、特別にこの問題を取り上げてみました。
第20回 ラグランジュの未定乗数法 [ネコ騙し数学]
第20回 ラグランジュの未定乗数法
定理 (ラグランジュの未定乗数法)
関数φ(x,y)は点(a,b)の近傍でC¹級でφ(a,b)=0で、(a,b)は特異点でないとする。このとき、φ(x,y)=0の条件のもとでf(x,y)が点(a,b)で極値をとり、かつ全微分可能ならば、ある定数λがあって、次が成り立つ。
![]()
【証明】
点(a,b)は特異点でないので、または
。
いま仮にとすると、このとき、陰関数定理よりφ(x,y)=0はx=aの近傍でb=ψ(a)でC¹級な陰関数y=ψ(x)が存在する。
とおくと、g(x)はx=aで極値をとるからg'(a)=0。
また、
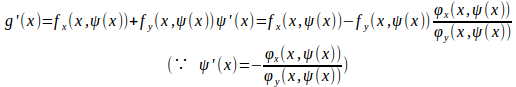
だから、
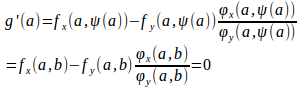
ここで、
とおくと、
(証明終)
問題1 x²+y²=1のとき、f(x,y)=x+yの最大値、最小値をと求めよ。
【解】
曲線φ(x,y)=x²+y²–1= 0は有界閉集合で、f(x,y)は連続だから最大値、最小値をもつ。
だから
となるのは(x,y)=(0,0)であるが、φ(0,0)=−1だから、φ(x,y)は特異点をもたない。
このとき、f(x,y)の最大値、最小値は極値だから、ラグランジュの未定乗数法より
とおくと、極値を取る点では
でなければならない。
λ≠0だから、①と②より
③に代入すると、
よって、
したがって、最大値は
最小値は
である。
(解答終)
【別解1」
x²+y²=1だから、x=cosθ、y=sinθ(0≦θ<2π)とおくと、三角形の合成公式より
よって、
θ=π/4、すなわち、x=y=1/√2のときに最大で最大値は√2で、
θ=5π/4、すなわち、x=y=−1/√2のときに最小で最小値は−√2である。
(別解1終)
【別解2】
x+y=kとおくと、直線x+y=kが円x²+y²=1に接するときに、kは最大、最小になる。
これは、原点と直線x+y–k=0の距離=1のときだから、
(別解2終)
問題2 4x²+y²=4の条件のもとで、f(x,y)=x+yの極値を求めよ。
【解】
曲線4x²+y²=4は有界閉集合で、f(x,y)は連続だからこの有界閉集合で最大値、最小値をもつ。
φ(x,y)=4x²+y²–4=0とおくと、だから、
となる点は(x,y)=(0,0)であるが、φ(0,0)=−1≠0なので、φ(x,y)=0は特異点をもたない。
ラグランジュの未定乗数法より
とおくと、
λ≠0だから、①と②より
③式に代入すると、
よって、
したがって、(x,y)=(1/√5,4/√5)のときにfは極大で極大値は√5、(x,y)=(−1/√5,−4/√5)のときにfは極小で極小値は−√5である。
(解答終)
【別解】
直線x+y=kが楕円4x²+y²=4に接するときにkは最大・最小。
y=k–xとおき、4x²+y²=4に代入すると、
(別解終)
問題3 x³+y³=3xyの条件のもとでf(x,y)=x²+y²の極値を求めよ。
【解】
φ(x,y)=x³+y³–3xy=0とおくと、 だから、(x,y)=(0,0)は特異点。
f(x,y)=x²+y²は非負だから(x,y)=(0,0)のときにf(0,0)=0で、このときに極小である。
(x,y)≠(0,0)とする。
ラグランジュの未定乗数法より
とおくと、
①、②より
x=yのとき、x³+y³=3xyより
陰関数定理より(x,y)=(3/2,3/2)でだから、x=2/3の近傍でyはxの関数である。
極値の判定をするために、f(x,y)=x²+y²とx³+y³=3xyをxで微分すると、
![]()
よって、(x,y)=(3/2,3/2)のとき
③と④の両辺をxで微分すると、
よって、(x,y)=(3/2,3/2)のとき、⑤式より
となり、(x,y)=(3/2,3/2)のとき、fは極大で、
x+y+xy=0のとき、x³+y³=3xyより
x+y=0とx³+y³=3xyより(x,y)=(0,0)。
以上のことより、(x,y)=(0,0)のとき、f(x,y)は極小で、極小値は0。
(x,y)=(3/2,3/2)のとき、f(x,y)は極大で、極大値は9/2。
(解答終)
第19回 陰関数の極値(偏微分) [ネコ騙し数学]
第19回 陰関数の極値
点(x₀,y₀)を含む領域Dでf(x,y)はC¹級であるとする。陰関数定理より、ならば、x₀の近傍でf(x,y)=0で定めるC¹級の陰関数y=φ(x)がただ一つ存在し、
である。
(1)式をさらにxで微分すると、
ここで、
したがって、f(x,y)がDでC²ならば、
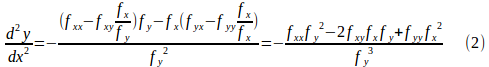
である。
問題1 関係式x²–2xy–y²=1で定まる陰関数についてを求めよ。
【解】
f(x,y)=x²–2xy–y²–1とおくと、 だから、
だから
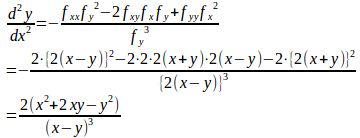
(解答終)
次に、f(x,y)をC²級とし、f(x,y)=0で定まるC²級の関数y=φ(x)の極値について考えることにする。
y=φ(x)がx=x₀で極値を取るとすると、陰関数定理より
また、y=φ(x₀)で極値をとるためには、
したがって、(2)式より、x=x₀におけるd²y/dx²の値は
![]()
となる。
よって、
のときy=φ(x₀)は極小となり、
のときに極大となる。
以上のことをまとめると、次の定理になる。
定理
f(x,y)をC²級の関数とし、y=φ(x)をf(x,y)=0の定める陰関数とする。
φがx=x₀で極値y₀=φ(x₀)を取るならば、
で、
のときy₀は極大値で、
のときy₀は極小値である。
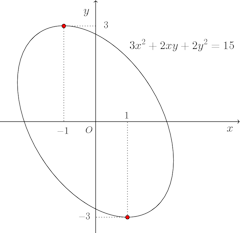
問題2 3x²+2xy+2y²=15の定める陰関数yの極値を求めよ。
とおくと、
3x²+2xy+2y²–15 =0に代入すると、
だから
(x,y)=(−1,3)のとき
(x,y)=(1,−3)のとき
よって、
yは、x=−1のとき極大値3、x=1のとき極小値3をとる。
(解答終)
この程度の問題ならば、3x²+2xy+2y²=15をxに関する2次方程式と考え、2次方程式の判別式を使って解くこともできる。
【別解】
xに関する2次方程式3x²+2yx+2y²–15=0は実根を持たなければならないので、その判別式をDとすると、
y=−3のとき
同様に、y=3のときx=−1。
したがって、yは、x=−1のとき極大値3、x=1のとき極小値1を取る。
(別解終)
宿題 3x²+2xy+2y²=15で定まる陰関数yの極値を、1変数関数の微分を用いて求めよ。
この問題を自分で解くと、紹介した定理の有り難みがよく分かる!!
第18回 陰関数の種々の計算問題 [ネコ騙し数学]
第18回 陰関数の種々の計算問題
問題1 次の関係式が定めるxの関数yの第1次導関数、第2次導関数を求めよ。
【解】
(1) x²+y²=1の両辺をxで微分すると、
y≠0のとき
(2) の両辺をxで微分すると、
のとき、つまり、x+y≠0のとき、
(解答終)
 問題2 曲線x²+xy+y²=3の点(1,1)における接線を求めよ。
問題2 曲線x²+xy+y²=3の点(1,1)における接線を求めよ。
【解】
x²+xy+y²=3の両辺をxで微分すると、
よって、x+2y≠0ならば、
(x,y)=(1,1)を代入すると、
したがって、接線の方程式は
(解答終)
f(x,y)をC¹級の関数とし、点(x₀,y₀)を曲線f(x,y)=0上の点、そして、または
であるとする。
いま仮にとすると、陰関数定理より、点x₀の近傍内にある曲線の部分は、f(x,y)=0で定まるただ1つの陰関数y=φ(x)で表される。
このとき、
が成立するので、接線の方程式は
であり、曲線上の点(x₀,y₀)における曲線f(x,y)=0の接線はただ1本である。
この結果を用いるならば、問題2は次のように解くこともできる。
【別解】
f(x,y)=x²+xy+y²–3=0とすると、
f(x,y)の点(1,1)における偏微分係数だから、曲線f(x,y)=0の曲線上の点(1,1)における接線の方程式は、(1)より、
(別解終)
【解】
x²–xy+y²=3の両辺をxで微分すると、
よって、y'=0になるのはy=2xのとき。
これをx²–xy+y²=3に代入すると、
よって、yの陰関数の極値になる点は(x,y)=(1,2)、(−1,−2)。
極値の判定をするために、①の両辺をxで微分すると、
極値を取る点ではy'=0だから、
したがって、
(x,y)=(1,2)のときy''=−2/3<0となり、このとき極大、
(x,y)=(−1,−2)のとき、y''=2/3>0となり、このとき極小。
以上のことより、x=1のときyは極大で極大値は2、x=−1のときyは極小で極小値は−2である。
(解答終)
【別解】
xに関する2次方程式x²–yx+y²–3=0のxの解は実数でなければならないから、2次方程式の判別式をDとすると、
でなければならない。
y=−2のとき
y=2のとき
よって、
x=−1のときyは極小で極小値は−2。
x=1のときyは極大で極大値は2。
(別解終了)
2次方程式の判別式を使わず、その元となる平方完成を用いると、
【別解2】
よって、
x=−1のときyは極小で極小値は−2。
x=1のときyは極大で極大値は2。
(別解終了)
陰関数定理の補足 [ネコ騙し数学]
陰関数定理の補足
f(x,y)はC¹の関数であるとする。
陰関数定理の主張は、
であるならば、x₀の近傍でC¹級の陰関数y=φ(x)がただ1つ存在し、
であるということ。
または
という条件は、あくまで、関係式f(x,y)=0で定まるC¹級の陰関数y=φ(x)またはx=ψ(y)が存在することの十分条件であって、この条件を満たしていなくても、C¹級の陰関数y=φ(x)またはx=ψ(y)が存在することがある。このことは、次の問題を解けばわかる。
問題1 x³–2xy+y²=0によって定まるC¹級の陰関数y=φ(x)とφ'(0)を求めよ。
【解】
 f(x,y)= x³–2xy+y²とおくと、
f(x,y)= x³–2xy+y²とおくと、だから、曲線x³–2xy+y²=0上の点(0,0)での偏微分係数は
。
つまり、(0,0)は曲線x³–2xy+y²=0の特異点。
したがって、陰関数定理から、x₀=0近傍で、x³–2xy+y²=0によって定まるC¹級の陰関数y=φ(x)が存在するかどうかはわからない。
x³–2xy+y²=0をyについて解くと、
x=0におけるy₁とy₂の右側、左側微分係数を求めると、
そこで、
と定めると、φ'(0)=2となる。
また、
と定めると、φ'(0)=0になる。
(解答終)
問題2 x³–2xy+y²=0によって定められる陰関数
と
がx=0で微分可能であることを示せ。
【解】
まず、y=φ₁(x)がx=0で微分可能であることを示す。
h>0のとき、
h<0のとき、
したがって、y=φ₁(x)はx=0で微分可能で、である。
次に、y=φ₂(x)がx=0で微分可能であることを示す。
h>0のとき、
h<0のとき
したがって、y=φ₂(x)はx=0で微分可能で、
(解答終了)
y=φ₁(x)とy=φ₂(x)が開区間(−∞,1)からx=0を除いた点で微分可能なのは明らか。そして、上の問題からx=0で微分可能だから、(−∞,1)でφ₁、φ₂ともに微分可能ということになる。
関係式f(x,y)=0で定まるC¹級の陰関数 [ネコ騙し数学]
関係式f(x,y)=0で定まるC¹級の陰関数
f(x,y)を
とする。
原点(0,0)の近傍で、関係式f(x,y)=0が定めるC¹級の陰関数y=φ(x)について考えることにする。
だから、原点(0,0)ではとなり、陰関数定理からC¹級の陰関数y=φ(x)の存在の有無を確かめることはできない。
そこで、次のようにyについて解き、
としてみる。
しかし、このように定めると、下図を見ると明らかなように、x=0で曲線y=φ₁(x)、y=φ₂(x)ともに尖っており、x=0で微分可能ではなく、ともにx=0の近傍でC¹級ではない。したがって、この関数は、x=0でf(x,y)=0が定めるC¹級の陰関数y=φ(x)ではない。-001-1d00c.png)
しかし、
とすると、このどちらもx=0で微分可能であり、また、x=0の近傍で滑らかな曲線になっているので、C¹級ということになる。-d53b7.png)
また、この陰関数を曲線y²=x²(x+a)の2つの枝に選ぶと、曲線y²=x²(x+a)は原点(0,0)において接線を2本引くことができる。
この他にも、この問題の場合、x=0のときに陰関数が極値になるかどうかの違いが出てくるので、注意が必要である。
第17回 陰関数定理 [ネコ騙し数学]
第17回 陰関数定理
定義 (陰関数)
xとyに関する関係式f(x,y)=0に対して、関数y=φ(x)が
を満たすとき、y=φ(x)をf(x,y)=0によって定まる陰関数という。
例えば、f(x,y)=x²–y²–1= 0 とする。このとき、
とすれば、
![]()
となるので、と
は関係式f(x,y)=x²–y²–1= 0 で定まる陰関数である。
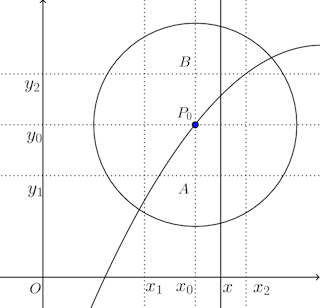
定理18 (陰関数定理)
点(x₀,y₀)を含む領域でf(x,y)はC¹級とする。
ならば、点(x₀,y₀)を含む近傍でf(x,y)=0の定めるC¹級の陰関数y=φ(x)がただ1つ定まり、次の関係が成り立つ。
とする。
関数f(x,y)はC¹級だから点(x₀,y₀)のある近傍でである。
x=x₀で固定すると、だからf(x₀,y)はyに関して単調増加。
A(x₀,y₁)を近傍内の点とすると、y₁<y₀でf(x₀,y₁)<0、B(x₀,y₂)、y₀<y₂でf(x₂,y₂)>0である。
x₁≦x≦x₂において
f(x,y)は連続で単調増加だから、中間値の定理よりy₁<y<y₂となるyがただ1つ存在する。そのyの値はxの関数で、それをy=φ(x)とすればよい。
次に、y=φ(x)が連続であることを示す。α∈[x₁,x₂]、β=φ(α)とし、任意のε>0に対して
とすると、
y₁≦y≦y₂のとき、だから
はx=αで連続であるから、あるδ>0があって、
また、だから
よって、
となり、y=φ(x)はx=αで連続である。
f(x,y)はC¹級だから平均値の定理より
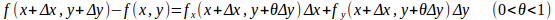
となるθが存在する。
また、f(x+Δx,y+Δy)=f(x,y)=0だから、Δx≠0のとき
は連続だから、Δx→0のとき、
(証明終)
3変数関数についても陰関数定理が成り立つ。
定理19
関数f(x,y,z)が点(a,b,c)の近傍でC¹級ならば、点(a,b)を含む開集合D上でC¹級の関数z=φ(x,y)で
を満たすものがただ1つ存在し、
である。
問 次の問に答えよ。
(1) 点(1/√2,−1/√2)の近傍で、関係式x²+y²=1で定まる陰関数yを求めよ。
(2) 点(1,0)の近傍で、関係式x²+y²=1で定まる陰関数を求めよ。
【解】
(1) f(x,y)=x²+y²–1=0とおくと。
よって、
となり、陰関数定理より、点(1/√2,−1/√2)の近傍で 関係式x²+y²=1で定まる陰関数y=φ(x)が存在する。
とすると、
となり不適。
とすると、
よって、
(2) 点(1,0)における偏微分係数は
だから、陰関数定理により点(1,0)の近傍で 関係式x²+y²=1で定まる陰関数x=φ(y)が存在する。
x²+y²=1をxについて解くと
(x,y)=(1,0)を満たすのはだから、これが点(1,0)の近傍で関係式x²+y²=1で定まる陰関数である。
(解答終)
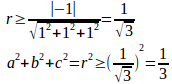
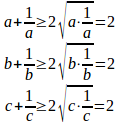
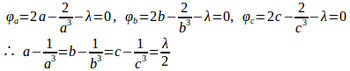
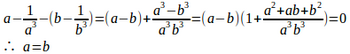
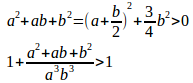
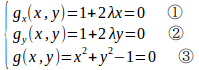
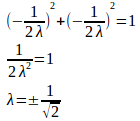
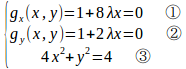
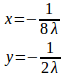
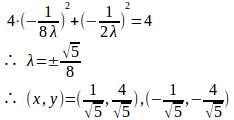
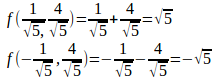
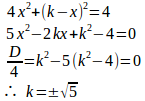
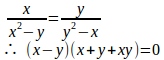
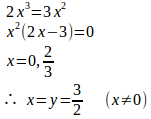
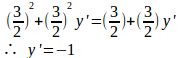
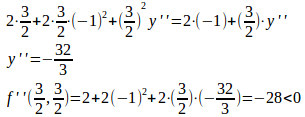
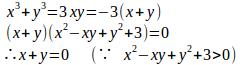
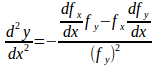
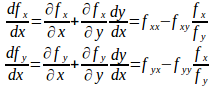
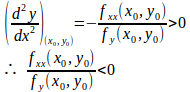
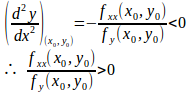





-002.png)