偏微分の簡単なドリル [ネコ騙し数学]
最近、２次曲線を取り上げ、肝心の偏微分の記事をブログにアップしていない。
そこで、お前らに一つ尋ねるけれど、次の偏微分くらいは簡単に求められるんだろうな。
問題 次の関数を偏微分しなさい。
次の定理を使うと、比較的簡単に上の関数の偏微分を求めることができる。
定理 関数f(u)が微分可能で、u=φ(x,y)が偏微分可能ならば、
である。
ただ、この定理を使って実際に計算する場合は、公式（A)よりも、z=f(u)とおき、
を使ったほうが間違いにくいのだろう。
（１）の場合は、z=f(u)=√u、u=x²+y²とすると、
だから、
になる。
（２）の場合、
とおけば、
だから、
になる。
なお、
２次曲線の離心率 [ネコ騙し数学]
２次曲線の離心率
放物線の定義は、「直線（準線）と直線上にない定点（焦点）との距離が等しい点の軌跡」であり、これは「準線からの距離と焦点からの距離の比が１：１である点の軌跡」と言い換えることができる。
そこで、これをさらに一般化し、
「準線からの距離と焦点からの距離の比が１：eである点の軌跡」
について考えることにする。
準線をy軸とし、焦点Fの座標を(c,0)とすると、点P(x,y)と準線との距離は｜x｜、焦点Fと点Pとの距離は
になるので、
この両辺を２乗すると、
e=1のときは
e≠1のとき
0<e<1のとき、e²–1<0だから
e>1のとき
したがって、
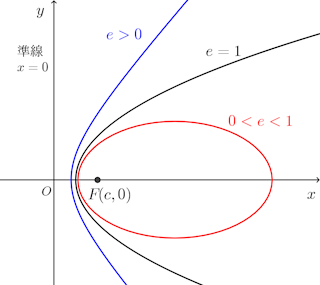
0<e<1のとき楕円、e=1のとき放物線、e>1のとき双曲線である。
このeを離心率という。
楕円、双曲線の中心が原点に一致するよう、x軸方向に
平行移動すると、（３）式は
したがって、楕円
の離心率eは、
から
と求められる。
また、このとき、（４）式は
となるので、双曲線の離心率eは
から
と求められる。
タグ：数学基礎
