ベクトル関数とその微分 [ネコ騙し数学]
ベクトル関数とその微分
実数Rの部分集合Dに属する点tに対して、実関数x(t)、y(t)、z(t)が与えられているとき、ベクトル(x(t),y(t),z(t))を考えることができ、このベクトルF(t)=(x(t),y(t),g(t))をDからR³への1変数ベクトル値関数、または、ベクトル関数という。
Lを定ベクトル、t₀を一定の値とするとき、
ならば、tがt₀に限りなく近づくとき、F(t)はLに限りなく近づくといい、また、LはF(t)の極限といい、
であらわす。
イプシロン・デルタ論法で書くならば、
任意のε>0に対して、あるδ>0があって
が成り立つとき、
とあらわす。
また、
が成り立つとき、F(t)はt=t₀で連続であるという。また、区間Iのすべての点でtで連続であるとき、F(t)はIで連続であるという。
イプシロン・デルタ論法による、ベクトル関数F(t)のt=t₀における連続の定義は次の通り。
任意のε>0に対して、あるδ>0があって
が成り立つとき、F(t)はt=t₀において連続であるという。
ベクトル関数F(t)に関して、次の極限
が存在するとき、F(t)はt=t₀で微分可能という。また、この極限値Aをt=t₀における微分係数といい、
であらわす。
定理
とすると、次が成立する。
(ⅰ)
(ⅱ) F(t)は連続⇔x(t)、y(t)、z(t)は連続
(ⅲ)
この定理はほとんど明らかだと思うので、(ⅰ)だけを証明することにする。
【略証】
(ⅰ) ならば、
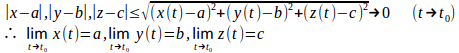
逆に、
ならば

(証明終)
ベクトル関数の微分については、実関数の微分と同様に次の公式が成り立つ。すなわち、A=A(t)、B=B(t)をtのベクトル関数m=m(t)をtのスカラー関数とすると、
である。
例1 Cが一定のベクトルのとき、
例2 mが定数のとき、
問題1 Aをtのベクトル関数とするとき、次のことを示せ。
(1)
ここで、A²=A・Aとする。
(2) |A|が一定であるとき、A とは直交する。
【解】
(1)
(2) |A|は一定だから、A²=A・A=|A|²も一定。
したがって、
また、(1)の結果より
よって、A とは直交する。
(解答終)
問題2
【解】
![]()
(解答終)
問題3 A(t)の微分係数をAの方向とこれに垂直な方向とに分解せよ。
【解】
Aと同じ方向の単位ベクトルをa、Aの大きさをAとすると、
aは単位ベクトルだから問題1より、aとは直交するので、
である。
(解答終)
A(t+Δt)とA(t)のなす角をΔθ、単位ベクトルaの増分をΔaとすると、
と同じ方向の単位ベクトルをbとすると、
だから、問題3の(1)は
である。