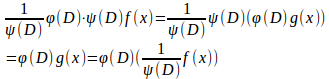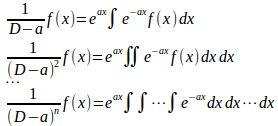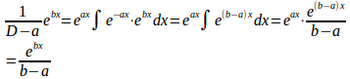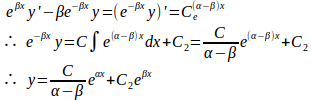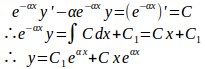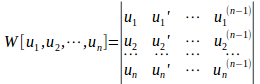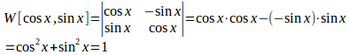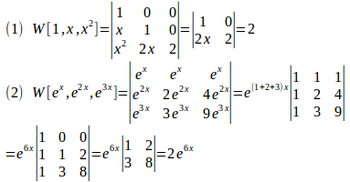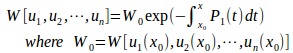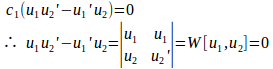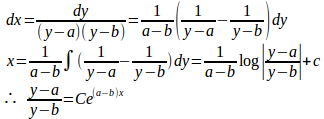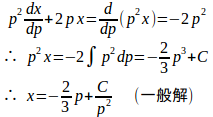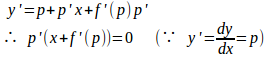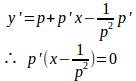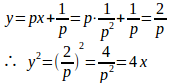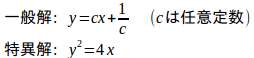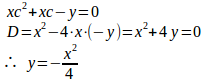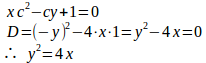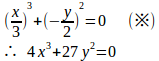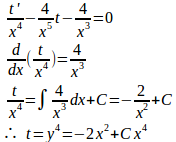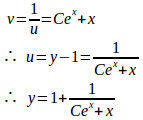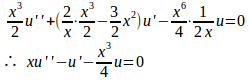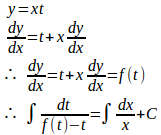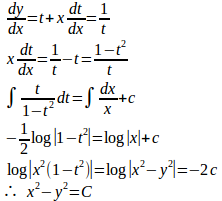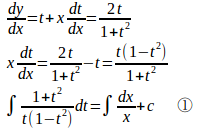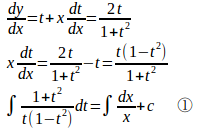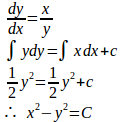第13回 演算子Dを用いる方法の注意点 [ネコ騙し数学]
第13回 演算子Dを用いる方法の注意点
次の微分方程式があるとする。
微分演算子Dを用いると、
と、形式的に、この微分方程式の特殊解を得ることができる。
ここで、
とおくと、
となるが、φ(a)=0だから、この公式を使うことが出来ない。
だから、この場合は定義に立ち返って、
と計算するか、公式
を用いて特殊解を求めなければならない。
①の場合、b=a、f(x)=1とおくと、
問 次の微分方程式を解け。
【解】
同次方程式
の特性方程式は
したがって、この方程式の基本解はで、一般解は
である。
で、φ(D)=D–2とおくと
よって、
したがって、この微分方程式の一般解は
(解答終)
第11回 定数係数の線形非同次微分方程式の解法2 [ネコ騙し数学]
第11回 定数係数の線形非同次微分方程式の解法2
演算公式2
ρ(D)をDの有理式、aを定数とするとき、次の公式が成り立つ。
ここで、iは虚数単位、すなわち、i²=−1。
問題1 φ(D)をDの整式、aを定数とするとき、次の公式を証明せよ。
(1)
だから、
とすると、
(2) ライプニッツの定理より
したがって、
(3)、(4)
オイラーの公式より
よって、
この実部と虚部をとれば得られる。
(解答終)
問1 次の微分方程式の1つの特殊解を求めよ。
【解】
微分方程式の特殊解をy₀とする。
(1)
ここで、
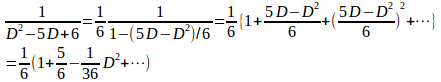
とマクローリン展開し
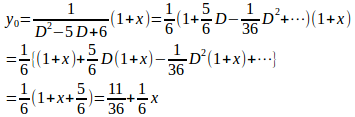
(2)
ここで、
とおくと、公式(1)より
(解答終)
同次方程式
の一般解は
だから、問1の非同次方程式の一般解は
である。
また、
の特殊解は、
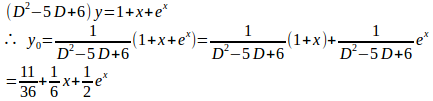
したがって、この微分方程式の一般解は、
である。
問2 次の微分方程式の1つの特殊解を求めよ。
【解】
微分方程式
を考える。
ここで、
とすると、
オイラーの公式より
だから、
![]()
①の実(数)部が
が(1)の特殊解で、
②の虚(数)部が
が(2)の特殊解、
したがって、
(解答終)
第10回 定数係数の非同次線形方程式 [ネコ騙し数学]
第10回 定数係数の非同次線形方程式
定数係数の線形方程式で、右辺が0でない場合、
![]()
を非同次という。これは右辺が0の場合の一般解を求め、1つの特殊解が求められると完全に解くことができる。このため、xによる微分演算子Dを導入し、Dの形式的計算により、
を求める方法を考える。
を用いると、(1)は
となる。φ(D)はDの形式的多項式であるが、定数と交換可能、すなわち、
![]()
であるから、たとえば、
![]()
などと計算することができる。
そこで、割り算を次のように定義し、分数式の計算も可能なようにする。
定義
φ(D)をDの整式とするとき
をφ(D)g(x)=f(x)を満たす関数g(x)と定義する。ただし、φ(D)g₀(x)=0となる関数g₀(x)の違いは無視することにする。
このように定義すると、たとえば、
ただし、
すなわち、f₀(x)=定数の違いは無視する。
定理
φ(D)とψ(D)をDの整式とするとき、
が成り立つ。
【証明】
とすると、
よって、
(証明終)
したがって、Dの分数式も整式の同様に計算できる。
計算公式
aを定数とするとき
問題1 次のことを証明せよ。
と
【証明】
とおくと、
これはg(x)についての1回線形微分方程式だから
であるが、は
の一般解なのでこれを省くと、
である。
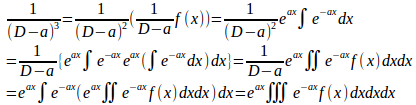
(証明終)
同様にして、(数学的帰納法より)
が成立する。
問1 次の問に答えよ。
(1) a、b(a≠b)が定数のとき、次のことを示せ。
(2) (1)の結果を利用し、次の微分方程式の特殊解を求め、一般解を求めよ。
【解】
(1)
(2) 同次微分方程式
の一般解は。
(1)より、
は非同次方程式
の特殊解だから、一般解は
(解答終)
公式
ρ(D)をDの有理式、がxのn次の整式とするとき、
![]()
である。
ただし、ρ(0)の値が有限で、マクローリン展開が
とする。
問題2 ρ(r)をrの有理式でr=0で分母は0でないとし、P(x)は3次の整式とするとき、
であることを示せ。
ただし、r=0の近傍で、
とする。
【証明】
ρ(0)は有限でr=0で
と展開可能。
したがって、
(証明終)
問2
(1)
であることを利用して、
であることを導け。
(2) (1)の結果を用いて、
を求めよ。
(3) 次の線形同次微分方程式を解け。
【解】
(1)
x²=tとおくと
(2)
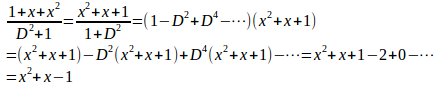
(3) 線形同次方程式
の一般解は
(2)より、x²+x–1は、非同次方程式
の特殊解なので、一般解は
(解答終)
第9回 2階線形微分方程式(定数係数)の解法 [ネコ騙し数学]
第9回 2階線形微分方程式(定数係数)の解法
§1 線形常微分方程式(定数係数)の解法
2階同次線形微分方程式(定数係数)の一般形は
である。
を(1)の(基本)解とすると,
だから、
だから、
でなければならない。この2次方程式を(1)の特性方程式といい、この2次方程式の解を特性解、特性根という。
(1)の特性方程式(2)の解をα、βとすると、2次方程式の解と係数の関係より、
である。
したがって、(1)は
である。
したがって、
となり、y'–βy の一般解は、
となる。
α≠βの場合
(3)式の両辺にを掛けると、
とおくと、(1)の一般解は
α=β(重根)の場合
α=βだから(3)式は
両辺にを掛けると、
C=C₂とすると、一般解は
となる。
特性根が虚根p±qiのとき、
問題1 次の微分方程式を解け。
【解】
(1) 特性方程式は、
よって、一般解は
(2) 特性方程式は
したがって、一般解は
(3) 特性方程式は
よって、
(解答終)
n階線形微分方程式の一般形は、定数係数の場合、
![]()
がを解にもつとすれば、
そこで、
とおけば、
となり、
を満たすとき、は(3)の解の1つとなる。
(4)を(3)の特性方程式といい、その解を特性解、特性根という。
問題2 次の微分方程式を解け。
【解】
(1) 特性方程式は
![]()
よって、一般解は
(2) 特性方程式は
よって、一般解は
(解答終)
§2 2階線形非同次常微分方程式(定数係数)
2階線形非同次微分方程式の一般形は
である。
(5)の一般解は、同次線形方程式(1)の一般解と(5)の特殊解の和で表されるので、まず、同次方程式(1)の一般形を求め、何らかの方法で非同時方程式(5)の特殊解を求めたのち、それを先に求めた同次方程式の一般解に加えればよい。
問題3 次の微分方程式を解け。
【解】
(1) 同次方程式y''–2 y –y=0の特性方程式
だから、この一般解は
非同次方程式
の特殊解がy=ax²+by+cであるとすると、
だから、これを①に代入すると、
ゆえに、a=−1、b=1、c=−1。
したがって、y=–x²+x–1は①の特殊解。
だから、①の一般解は
(2) 同次形方程式y''–y=0の一般解は
非同次方程式
の特殊解がy=Acos+Bsinxであるとすると、
だから、①に代入すると、
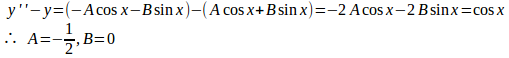
よって、
は①の特殊解である。
したがって、①の一般解は
(解答終)
第8回 線形微分方程式とロンスキアン [ネコ騙し数学]
第8回 線形微分方程式とロンスキアン
未知関数y(x)のn階線形常微分方程式の一般形は
である。
Q(x)=0のとき同次、Q(x)≠0のとき非同次という。
左辺のL[y]は関数から関数への写像なので、実数から関数への写像へと区別するために、[]を用いる。また、y(x)に対する微分演算を含むので微分演算子または微分作用素といい、線形演算子である。
定義
次の2つの性質を満たす演算子を線形演算子という。
(1)式の1つの解をy₀とすると、u=y–y₀は
であるから、uは同次微分方程式
の解である。
これを(1)の補助微分方程式といい、その一般解を余関数という。
また、このことから、(1)の一般解は、(1)の1つの解と余関数の和で表されることになる。
定義
n–1回微分可能なn個の関数
に対して、次の行列式をロンスキー(Wronski)の行列式、または、ロンスキアン(Wronskian)といい、
であらわす。
例
とすると、
問1 次の関数のロンスキアンを求めよ。
【解】
(解答終)
定理1 ![]() を、u₀を含む区間における微分方程式の解(2)とするとき、それらのロンスキアンは次式で与えられる。
を、u₀を含む区間における微分方程式の解(2)とするとき、それらのロンスキアンは次式で与えられる。
一般の場合の証明は難しいので、線形代数(行列式の計算法)の知識を必要しないn=2の場合について証明することにする。
【証明】(n=2の場合)
u₁、u₂を2階線形常微分方程式
の解とする。
ロンスキアンW
をxで微分すると、
![]()
になる。
u₁、u₂を2階線形常微分方程式(3)の解だから
これを①に代入すると、
よって、②の一般解は
したがって、
(解答終)
ロンスキアンWはxの関数になるので、これをW(x)と書くことにすると、この定理1から、区間I内の1点x₀におけるロンスキアンW(x₀)≠0ならば、Iで常にW(x)≠0であることになる。
定義
区間で、n個の関数について、全部が0でない定数
によって
になるとき、1次従属であるといい、そうでないとき1次独立であるという。
ならば、このn個の関数は1次独立である。
n個の関数が1次従属ならばW=0である。
n=2の場合について証明する。
【証明】
対偶法を用いて証明する。
u₁、u₂は1次従属とすると、同時に0でないc₁、c₂によって
となる。
両辺をxで微分すると、
すくなくともc₁、c₂の一方は0でないので、c₁≠0とする。
より、
よって、証明された。
(証明終)
定理3’ n階同次線形常微分方程式(2)のn個の解![]() に対して、xの区間で
に対して、xの区間で
ならば、このn個の解は1次従属である。
したがって、n個の解が1次独立のとき、そのロンスキアンは0でない。
定義 n階同次線形常微分方程式(2)のn個の1次独立の解の1組を、その基本解または基本系という。
例 は、2階同次線形常微分方程式
の基本解である。
は、2階同次線形常微分方程式
の基本解である。
定理4 n階同次線形微分方程式の一般解u(x)は、基本解![]() の任意の1次従属で表される。すなわち、
の任意の1次従属で表される。すなわち、
である。
定理4により、(3)の一般解yは
であり、(4)の一般解は
であることが保証される。
第7回 1階常微分方程式の補充問題 [ネコ騙し数学]
第7回 1階常微分方程式の補充問題
問題1 次の関数から任意定数A、B、Cを消去して微分方程式を作れ。
【解】
(1) y²=Cxの両辺をxで微分すると、
よって
(2) の両辺を微分すると、
①、②よりA、Bを求めると、
これを代入すると、
【別解】
行列式を用いてA、Bを消去すると
これから、
(解答終)
問題2 次の微分方程式を解け。
【解】
(1)
a≠bのとき
a=bのとき
(2) 同次形なのでy=txとおき、両辺をxで微分すると、
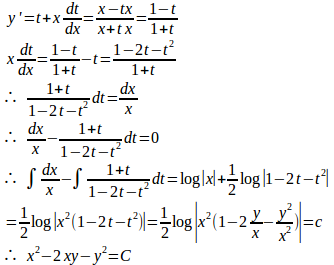
(3) 微分方程式y'+xy=0を解くと、
y=1はy'+xy=xの特殊解だから、y'+xy=xの一般解は
(4) 両辺にを掛けると、
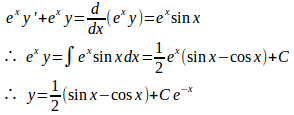
(解答終)
問題3 次の微分方程式を解け。
ここで、
【解】
(1) y=px+p³の両辺をxで微分すると、
p'=0すなわち、p=Cのとき、
3p²+x=0のとき、
だから両辺を2乗して、
(2) y=2px+p²の両辺をxで微分すると、
①をxの微分方程式に書き換えると、
両辺にp²を掛けると
p=0のとき、y=0(特異解)。
(解答終)
第6回 クレーロー型の微分方程式 [ネコ騙し数学]
第6回 クレーロー型の微分方程式
次の微分方程式
をクレーロー型の微分方程式という。
(1)式の両辺をxで微分すると、
となる。
したがって、p'=0またはx+f'(p)=0である。
p'=0のとき、pは定数だからこれをcとおくと、
となり、これが一般解である。
また、x+f'(p)=0、すなわち、x=−f'(p)のとき、
で、これは特異解である。
以上より、クレーローがの微分方程式(1)の解は、
である。
問1 次の微分方程式を解け。ただし、とする。
【解】
(1) y=px+p²の両辺をxで微分すると、
p'=0のとき、pは定数だからこれをp=cとおくと、一般解は
x+2p=0のとき、x=−2pとなり、これを用いて微分方程式y=px+p²からpを消去すると、特異解は
(2) 微分方程式の両辺をxで微分すると、
よって、p'=0のとき、
のとき、
したがって、
(解答終了)
クレーロー型の微分方程式の特異解は、一般解の包絡線である。
包絡線
αをパラメータとする曲線群f(x,y,α)=0の各曲線とただ1点で接する(共通接線)を曲線を、この曲線群の包絡線という。
f(x,y,α)を3変数のC¹級の関数とすると、曲線群f(x,y,α)=0の包絡線は、2曲線
の交点の軌跡で、この2式からαを消去した曲線に含まれる。
問2 次の曲線群の包絡線を求めよ。
【解】
(1) y=αx+α²の両辺をαで偏微分すると、
αを消去すると、
よって、包絡線は
(2) の両辺をαで偏微分すると、
よって、
![]()
したがって、包絡線は
(解答終)
以上のことより、問1のクレーロー型の微分方程式の特異解が一般解の包絡線になっていることが分かるだろう。
問3 クレーロー型の微分方程式
の特異解の表す曲線は、一般解y=cx+f(c)が表す直線族の包絡線であることを示せ。
【解】
のとき
だから直線と曲線は交点を有する。
この点における曲線の接線の勾配は
![]()
だから、直線y=cx+f(c)はこの曲線の接線である。
(解答終)
裏技として、「クレーロー型の微分方程式の一般解がcの代数方程式の場合、その判別式=0が特異解になる」というものがある。
たとえば、問1の(1)の場合、一般解は、y=cx+c²だから、
(2)の場合、一般解はだから両辺をc倍してcy=c²x+1とし、
と特異解を求めることができる。
問4 次の微分方程式を解け。
【解】
y=px+p²の両辺をxで微分すると、
ゆえに、p'=0またはx+3p²=0。
p'=0のとき、p=cで、一般解は
x=−3p²のとき、
この2式からpを消去すると、特異解は
(解答終)
【別解】
一般解はy=cx+c³だから
cについての3次方程式だから、その判別式=0とすると、特異解は
(別解終了)
(※)
3次方程式x³+px+q=0の判別式Dは
第5回 ベルヌーイ形、リッカチ形の微分方程式 [ネコ騙し数学]
第5回 ベルヌーイ形、リッカチ形の微分方程式
§1 ベルヌーイ形
をベルヌーイ形の微分方程式という。
(1)の両辺をで割ると、
とおき、この両辺をxで微分すると
となるから、tの線形の微分方程式
を得る。
この微分方程式を解くことによって、ベルヌーイ形の微分方程式(1)を解くことができる。
問題1 次の微分方程式を解け。
【解】
(1) この微分方程式はn=2のときのベルヌーイ形の微分方程式。
両辺をy²で割ると、
そこで、
とおき、両辺をxで微分すると、
したがって、①は
となる。
よって、
(2) この微分方程式はn=−3のときのベルヌーイ形の微分方程式。
両辺をy⁻³で割ると、すなわち、y³をかけると、
そこで、
とおき、両辺をxで微分すると、
よって、①は
両辺をx⁴で割ると、
(解答終)
§2 リッカチ形
y(x)についての1階微分方程式
をリッカチの微分方程式という。
これは一般に解くことはできないが、1つの特殊解y₁が既知であるとき次のように解くことができる。
y₁は(2)の特殊解だから、
(2)の両辺を上の式で引くと、
ここで、
とすると、
これはuについてのベルヌーイ形の微分方程式だから、解くことができる。
問題2 次の微分方程式を解け。
【解】
y=1とすると、①は
したがって、y=1は微分方程式①の解である。
そこで、u=y–1とおくと、u'=y'。
よって、①は
これはn=2のベルヌーイ形なので、両辺をu²で割ると、
そこで、
とおき、両辺をxで微分すると、
よって、
微分方程式
の解は。
ここで、v=xとすると、
したがって、v=xは、②の特殊解。
よって、②の一般解は
(解答終)
問題4 次の問に答えよ。
(1) リッカチ形微分方程式
が変換
によって、u(x)についての2階の線形微分方程式になることを示せ。
(2) (1)の変換によって、微分方程式
を線形微分方程式に変換せよ。
【解】
(1) とおくと
よって、微分方程式は次のように変換される。
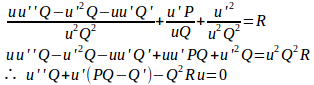
(2) とおくと、(1)より
第4回 1階線形微分方程式の解法 [ネコ騙し数学]
第4回 1階線形微分方程式の解法
1階線形微分方程式の一般形は
で与えられる。
定数変化法を用いて、(1)の一般解を求めることにする。
最初に、同次微分方程式の
の一般解を求めると、
が得られる。
この任意定数c₁を関数u(x)で置き換え、(1)を満たすようにu(x)を定める。
そこで、
を(1)に代入すると、
したがって、(1)の一般解は
である。
問題1 次の微分方程式を解け。
【解】
(1)
であるが、c₁=0として一般解を求める。
公式(2)より
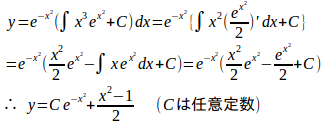
(2)
したがって、
よって、公式(2)より
(解答終)
問題2 次の微分方程式を解け。
【解】
(1)
(2)
だから、微分方程式
の両辺にをかける。
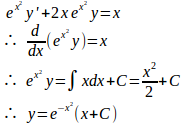
(解答終了)
公式(2)を用いて機械的に一般解を求めるより、問題2の(2)のように解いたほうがよいと思う。
問題3 一階線形微分方程式
の一つの特殊解がy₁であるとき、一般解は
であることを示せ。
【解】
一般解yと特殊解y₁は微分方程式(1)の解なので
①と②の両辺の差をとると、
φ=y–y₁とおくと、
この微分方程式の一般解は
よって、
(解答終了)
第3回 同次形 [ネコ騙し数学]
第3回 同次形
正規形の微分方程式
の右辺G(x,y)がy/xの関数であるとき、すなわち、
であるとき、同次形という。このとき、
とすると、次のように変数分離形に変換でき、一般解を求めることができる。
問題1 次の微分方程式を解け。
【解】
(1) 右辺は、t=y/xとおくと、f(t)=1/tの形になるので、同次形。
y=txとおくと、
(2) 右辺の分母分子をx²で割ると
よって、同次形。
y=txとおくと
ここで、
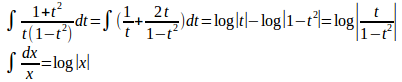
よって、
(3) 右辺をxで割ると
したがって、同次形。
y=txとおくと
ここで、
よって、①は

(解答終)
(1)は同次形の微分方程式として解いたけれど、これは変数分離法で
と解けばよい。
同次形ではないが、微分方程式
は、次のように変形することによって同次形の微分方程式に帰着させることができる。
(ⅰ) のとき
連立方程式
を満たす(x₀,y₀)が存在するので、
によって(X,Y)の微分方程式にする。すなわち、
により
と同次形の微分方程式に変換できる。
(ⅱ) のとき、
b≠0のとき、t=ax+byとおくと
b'≠0のとき、t=a'x+b'yとおくと
問題 次の微分方程式を解け。
【解】
(1) である。
連立方程式
を解くと、(x₀,y₀)=(1,1)。
x=X+1、y=Y+1とおくと、dx=dX、dy=dYだから
Y=Xtとおくと
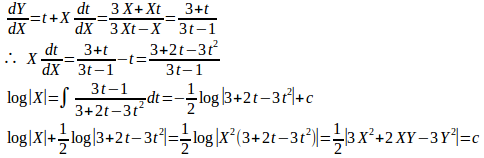
よって、
(2) だからt=2x–3yとおくと、微分方程式は
これを解くと
(解答終)