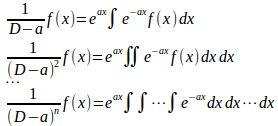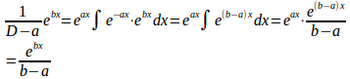第１０回 定数係数の非同次線形方程式

第１０回　定数係数の非同次線形方程式

 

定数係数の線形方程式で、右辺が０でない場合、

　　

を非同次という。これは右辺が０の場合の一般解を求め、１つの特殊解が求められると完全に解くことができる。このため、ｘによる微分演算子Dを導入し、Dの形式的計算により、を求める方法を考える。

　　

を用いると、（１）は

　　

となる。φ(D)はDの形式的多項式であるが、定数と交換可能、すなわち、

　　

であるから、たとえば、

　　

などと計算することができる。

そこで、割り算を次のように定義し、分数式の計算も可能なようにする。

 

定義

φ(D)をDの整式とするとき

　　

をφ(D)g(x)=f(x)を満たす関数g(x)と定義する。ただし、φ(D)g₀(x)=0となる関数g₀(x)の違いは無視することにする。

 

このように定義すると、たとえば、

　　

ただし、

　　

すなわち、f₀(x)=定数の違いは無視する。

 

定理

φ(D)とψ(D)をDの整式とするとき、

　　

が成り立つ。

【証明】

　　

とすると、

　　

よって、

　　

（証明終）

 

したがって、Dの分数式も整式の同様に計算できる。

 

計算公式

aを定数とするとき

　　

 

 

問題１　次のことを証明せよ。

　　

と

　　

【証明】

　　

とおくと、

　　

これはg(x)についての１回線形微分方程式だから

　　

であるが、は

　　

の一般解なのでこれを省くと、

　　

である。

　　

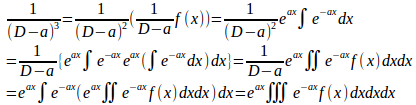
（証明終）

 

同様にして、（数学的帰納法より）

　　

が成立する。

 

問１　次の問に答えよ。

（１）　a、b（a≠b）が定数のとき、次のことを示せ。

　　

（２）　（１）の結果を利用し、次の微分方程式の特殊解を求め、一般解を求めよ。

　　

【解】

（１）

　　

（２）　同次微分方程式

　　

の一般解は。

（１）より、

　　

は非同次方程式

　　

の特殊解だから、一般解は

　　

（解答終）

 

 

公式

ρ(D)をDの有理式、がxのn次の整式とするとき、

　　

である。

ただし、ρ(0)の値が有限で、マクローリン展開が

　　

とする。

 

 

問題２　ρ(r)をrの有理式でr=0で分母は0でないとし、P(x)は３次の整式とするとき、

　　

であることを示せ。

ただし、r=0の近傍で、

　　

とする。

【証明】

ρ(0)は有限でr=0で

　　

と展開可能。

したがって、

　　

（証明終）

 

 

問２

（１）

　　

であることを利用して、

　　

であることを導け。

 

（２）　（１）の結果を用いて、

　　

を求めよ。

 

（３）　次の線形同次微分方程式を解け。

　　

【解】

（１）

　　

x²=tとおくと

　　

 

（２）

　　

 

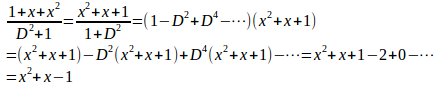
（３）　線形同次方程式

　　

の一般解は

　　

（２）より、x²+x–1は、非同次方程式

　　

の特殊解なので、一般解は

　　

（解答終）