同次関数とオイラーの定理 [ネコ騙し数学]
関数f(x,y)が任意の実数x、y、tに対して
が成り立つとき、f(x,y)をm次同次関数という。
fが1変数関数の場合は、
2変数以上の関数の場合は
である。
たとえば、
という関数があるとする。
このとき、
が成立するので、これは1次の同次関数である。
また、
とすると、
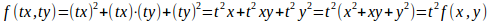
が成立するので、これは2次の同次関数である。
また、f(x,y)とg(x,y)を1次の同次関数とすると、
となるので、1次の同次関数の和は1次の同時関数である。
このことはほとんど明らかであるが、さらに、αを実数とすると、
が成立し、関数fの実数倍も1次の同次関数である。
問題1 f(x,y)をm次同次関数、すなわち、
が成り立つとき、次の問に答えよ。
(1)
(2) fがC¹級で
を満たすならば、fはm次同次関数である。
【解】
(1)
また、
だから、
よって、
t=1とすると、
である。
(2) とおきtで微分すると、
![]()
よって、φ(t)はtについて定数。
したがって、
(解答終)
問題1の(1)をオイラーの定理といい、(2)はオイラーの定理の逆である。
問題2
(1) m次同次関数z=f(x,y)において、とすると、
が成り立つことを示せ。
(2) (1)の結果を用いて、0次同次関数は、なる形をもつことを示せ。
【解】
(1)
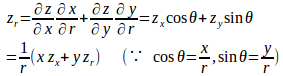
z=f(x,y)はm次同次関数だから、問題1より
したがって、
である。
(2) z=f(x,y)は0次同次関数だからm=0。
したがって、
したがって、zはだけの関数、つまり、y/xだけの関数となる。
よって、
(解答終)
なぜ、次の形の微分方程式を同次形というのか、その理由がわかってもらえるのではないだろうか。



