第59回 偏角の原理 [ネコ騙し数学]
第59回 偏角の原理
定理(偏角の原理)
関数f(z)は単一閉曲線Cで囲まれた閉領域Dで有理型であり、C上では正則で零点をもたないとする。f(z)はCの内部に極、零点
をもつとし、
を
の位数、
を
とすると、
【証明】
の1つの分枝を考えると、
となるので、
ここで、
とすると、はC上を1周しても値は変わらないので、
の変化量は、
と等しい。
よって、
f(z)がαをs次の極としてもつとき、αの近くで
とあらわせるので、
![]()
はαで正則だから、αは
の1次の極で
同様に、βはの1次の極で
となる。
Cの内部にあるの極は、
であるから、留数定理より
![]()
(証明終)
偏角の原理より、C上を反時計回りに1回転させると、w=f(z)はw平面上で1つの閉曲線をえがくことになり、
と書き直せる。この式の右辺はw平面上の閉曲線Γのz=0まわりの回転数をあらわす。
定理(Rouchéの定理)
f(z)、g(z)が単一閉曲線Cで囲まれた閉領域Dで正則であり、C上で
ならば、f(z)、g(z)はCの内部で同一個数の零点をもつ。ただしここでl位の零点はl個と数える。
【証明】
Cの内部にあるf(z)、g(z)の零点の個数をとする。仮定よりf(z)、f'(z)はC上に零点をもたないので、偏角の原理より
よって、
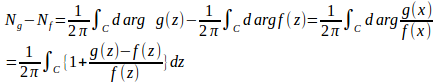
したがって、とおくと、仮定よりC上で|w|<1。
このとき、1+wは、zがC上を1周すると、w=1を中心とする半径1の内部で閉曲線Γをえがくことになり、w=0のまわりの回転数は0になる。
したがって、
(証明終)
偏角の原理の応用として、次に、代数学の基本定理の証明を与える。
定理 (代数学の基本定理)
複素数を係数とするn次の代数方程式
はn個の根をもつ。
【証明】
十分大きな正の数Rをとると、|z|<Rで
Cを|z|=Rとし、
とおき、 これに対してRouché(ルーシェ)の定理を用いると、f(z)はn個の零点をもつので、g(z)もn個の零点をもつことになり、定理は証明された。
(証明終)



