［境界方程式に関する留意点（ラプラス型）］

［境界方程式に関する留意点（ラプラス型）］

 

　前回でやっと、境界方程式の具体的な離散化方程式にたどり着きました(^^;)。

  

　しかし式(1)を具体的に解くためには、なおいくつかの手順が必要です。

（境界要素法って、なんて面倒(^^;)）

 

［1］境界条件の考慮

　式(1)の係数行列B，Hはn×nの正方行列で、既知ベクトルwの次元はn，未知ベクトルψとqの次元もnです。よってこのままでは、条件数n＜未知数の数2n、となり不定解しか出せません。これは偏微分方程式一般に言える事で、偏微分方程式の解は境界条件を与えて初めて一意に決まります。逆に言えば、境界条件を与えない限り、式(1)は不定解以外は出していけないのです。これもある意味、数学ってなんて正直・・・(^^;)。

 

　ラプラス型の境界条件では、解析領域境界C上の全ての点で、ψ(c)かq(c)の値を与える必要があります。よって、式(1)の未知数2n個のうちn個の値が与えられる事になり、条件数n＝未知数の数nとなって解けるようになります。

　最も簡単に境界条件を考慮する方法は、境界条件を表す式を補助方程式として追加してやる事です。

  

　ここでj＝j₁，j₂，・・・とk＝k₁，k₂，・・・は、ψ_jとq_kの値が与えられる節点番号で、最も一般的には規則性はないと思った方が無難です。Ψ_jとQ_kは境界条件により与える値です。

　式(2)の左辺全体を行列D₁，D₂で表します。また対応する右辺をベクトルd₁，d₂で表します。補助方程式を追加すると式(1)は、

  

の形になります。ψとqを合わせた未知ベクトルの次元は2n。(D₁ D₂)はn×2n行列なので、n×2nの(B H)と合わせて、全体は2n×2nの正方な係数行列になります。右辺の既知ベクトルはもちろん、d₁とd₂を合わせた次元はn，wの次元もnなので、全体で2nです。

　(D₁ D₂)を(B H)の上に置くのには理由があります。(D₁ D₂)に適当な行の並べ替えをかけると対角行列になり、(3)のψ，qに関する掃き出し計算が高速化されるからです。この性質は行の並べ替えを行わなくても保たれ、普通にやればよろしい！という事になります(^^)。

 

［2］ポテンシャル値問題

　境界条件として最もすっきりするのは、境界上の全ての点でψ(c)の値が与えられるか、q(c)の値が与えられた場合です。これらのケースでは式(3)の形を使うまでもなく、

  

のどちらかを解けばOKです。

　ところが式(5)のBは特異行列になります。つまり不定解しか出ません。これの理由は物理的事情です。ラプラス（ポアソン）方程式の解関数ψ(x，y)は、必ず何かの物理量のポテンシャル関数になります。そしてポテンシャル自体は物理量に対応せず、その微分だけが意味を持ち、ポテンシャル関数には定数分の不定性があるからです。すなわち式(5)は、不定解を出さなければならないのです。・・・数学ってなんて正直 (^^;)。

 

　物理的理由がはっきりしているので、対処は簡単です。ポテンシャル関数の不定性を固定してやります。例えば節点1に対してψ₁＝0という補助方程式を追加してやり、節点1に関する境界方程式を削除します。節点1の境界方程式とは、

 

  

の事です。実際には、ケースバイケースに最も都合の良い条件を選びます(^^)。

 

［3］滑らかな境界点と本当の角点の区別

　前回の結果では、境界方程式(1)の作成にあたって解析的積分式を使用すれば自然に、

  

の自由項k/2/π×ψが出てくるのでした。理論的には滑らかな境界の場合はk/2/π＝1/2で、角点の場合は角の内角をk_iとしてk_i/2/πです。

　という事は滑らかな境界に折れ線近似を行った場合、解析的積分式からは、近似折れ線間の角度k_iが現れてしまう事になります。近似が十分なら、k_iはπに近い数値にはなりますが。

　そこで通常は、強引にk_iをπにおきかえます。近似値より正確な真の値を使うんだから精度はより上がるはずだ！、という方針ですが、本当かなぁ～？(^^;)。実際にはBマトリックスを作った後に、滑らかな境界点に対応する対角成分iに(1/2－k_i/2/π)を足し込んでやるのが実用的です。またこれは計算プログラムが、滑らかな境界点と角点を区別する情報を持たねばならない事をも意味します。

 

［4］2重流速問題

　これは本当の角点で発生し、角点問題とも言われます。[1]で述べたように、各境界節点iには未知数への条件として境界方程式、

  

が一つだけ存在します。ψ_iかq_iが境界条件で与えられるので、全体として(ψ_j)や(q_j)を決定できる訳です。

　ところが角点には2個のq_iがあります。何故なら角点iの前後で外法線方向が不連続にジャンプするからです。q(c)はψ(x，y)の境界上での外法線方向微分値でした。角点iで2方向の外法線方向β⁽¹⁾とβ⁽²⁾があるなら（図-1）、当然外法線微分値q_iもq_i⁽¹⁾，q_i⁽²⁾と二つある事になります。これは、Hマトリックスとqベクトルの構成を、多少面倒にします。同一節点について、2つのq_iをみなければならないからです。

 

　もし境界条件でq_i⁽¹⁾とq_i⁽²⁾の両方が与えられるなら普通に解けますが、ψ_iとq_iの一方だったり、ψ_iしか与えられない場合には、節点iで未知数2個に対し境界方程式一本は条件不足です。これに対する対処法は、1980年代には色々考えられました。

 

1) 定数要素を用いる方法

　今まで線形近似でやって来ましたが、もちろん定数近似だって可能です。境界要素上で未知量ψ(c)やq(c)は変化しない定数だ、という近似です。境界積分の式からはcの（tの)一次の項が消え、計算はより簡単になります。その際の節点配置は通常、境界要素の中央に置かれ図-2のようになります。

　図から明らかなように定数要素を使えば、2重流速問題は避けて通れます。積分計算が簡単な事もあり実用的にもまずまずで、境界要素法の入門本ではけっこう推奨されてますが、線形近似くらいしたいよねぇ～、ってのが個人的本音です(^^;)。

 

2)陰解法を併用する方法

　陰解法の利点は、基本解の特異点が積分領域外にあるので、未知数を増やす事なくいくらでも境界方程式を立てられる事です。だったら目標角点での直接法の境界方程式をやめて、陰解法の境界方程式を角点で必要な数だけ追加すれば良いじゃない、という考えです（図-4）。

　この方法を使えば、今までやってきた積分式をそのまま流用でき、そのうえ精度的にも直接法と遜色ないんですよ。実用的には、とってもお奨めです。

　ところがやっぱり外部特異点の最適配置と定量的誤差評価は？、と始まりまして、理論家達には不評でした。特異点配置が自由過ぎて、評価できなかっただけなんだろ？と思っちゃう訳ですが、そういう訳で自分はときどき好んで使います(^^)。

 

3)方向微分の公式を用いる方法

　たぶん現在の主流はこれです。かつ入門本では、あまり見た事ありません(^^;)。

 

　2重流速問題に対処するためには、未知数を増やす事なく補助方程式を追加できれば良い訳です。この意味で3)陰解法併用法はすじが通っています。

　境界要素法では、未知関数ψとその微分値qを独立な近似関数として扱います。そこが微分値と関数値の精度が同等になる境界要素法の利点の一つです。有限要素法などでは微分値の近似関数は、関数値の近似関数を微分した関数で与えるので、微分値の近似次数は関数値より一段落ちるのが普通です。qはψの微分値なので理論的には本当は、qとψの間に一般的な制約条件が存在します。その意味では有限要素法の方が妥当なんです。

　まず節点j+1における要素kと要素k+1でのψ(c)の接線方向微分値p^(k)とp^(k+1)を、ψ_j，ψ_j+1，ψ_j+2で近似します（図-4）。長さはそれぞれL_kとL_k+1です。

(9)

　　

 

　(8)，(9)の接線微分の方向は図-4より、β^(k)＋π/2，β^(k+1) ＋π/2になります。従って節点j+1におけるx方向，y方向微分値ψ_x，ψ_yとは方向微分の公式から、以下の関係があります。

　　

 

　一方、図-4のβ^(k)，β^(k+1)方向の法線微分値q_j+1⁽¹⁾とq_j+1⁽²⁾についても同様に、

　　

 

が成り立ちます。(10)，(11)から(ψ_x，ψ_y)を消去すると（細く参照）、

　　

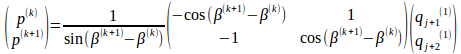
が得られます。さらに(8)，(9)を考慮して、

　　

です。これが節点j+1近傍で、関数値と外法線微分値が満たすべき制約条件です。当然の事ながらβ^(k+1)＝β^(k)の時は（滑らかな境界点の時は）、条件(12)はq_j⁽¹⁾＝q_j⁽²⁾＝q_jを与えるので不要です。これの意味するところは、あまり扁平な角点は頑張らずに、滑らかな境界点とみなした方が安全よ(^^)、という事です。

　境界条件で節点j+1両側のq_j+1が与えられた時、および片側のq_j+1およびψ_j+1がわかる時は、普通に境界方程式を立てます。片側のq_j+1だけ、またはψ_j+1しか既知でない時は、境界方程式をやめて条件(12)を使います。

 

　以上で計算プログラムに突入する準備は整ったぁ～！、と思ったら、まだ領域積分項の扱いがありましたね(^^;)。もぉ～、境界要素法って面倒くさいんだから・・・。

 

（執筆：ddt³さん）

 

補足

タグ：数値解析 境界要素法