差分法の基礎 [ネコ騙し数学]
差分法の基礎
f(x)を何回でも微分可能な関数とすると、テーラーの定理より、f(x)はx=aの近傍で
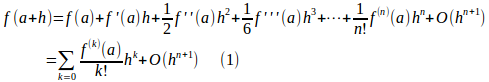
と展開することが可能である。
ここで、記号Oはランダウの（ビッグ）Oで
ある。
したがって、n=1,2,3とすると、
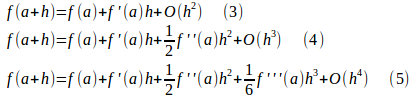
が成り立つ。
また、hを−hに置き換え、
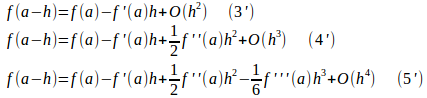
を得ることができる。
（３）式より、h≠0のとき、
となり、このことからf'(a)を
と近似したときの誤差はhのオーダー、
であると予想できる。
このことは、拡張された平均値の定理
より、h≠0のとき、
となり、f''(x)は
で連続だから
となるMが存在し、
となり、
と近似した誤差が｜h｜のオーダー程度であることが確かめられる。
f(x)がxの１次関数の時、
なので、
が成立すので、（６）は１次の精度である。
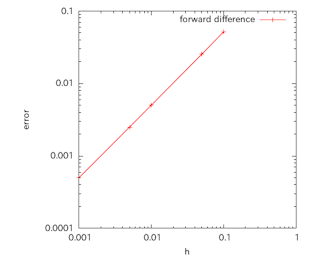
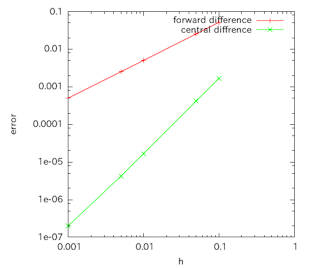
さらにa=0とし、hを変化させ、
と近似したときの誤差を求めてみると、右の図のようになる。
横軸にはh、縦軸に誤差をとり、対数グラフで結果を表している。
この直選の傾きが1であることから、（６）の近似式の誤差がhの１次オーダーであることが確かめられる。
このことを、
と表すことにする。また、f'(a)のこの近似式を前進差分と呼ぶことにする。
また、f'(a)を求めるために、（３）と（３’）の辺々を引くと、
が得られる。
（８）式で与えられるf'(a)の近似式を中心差分と呼び、この近似式の誤差はhの２次のオーダーであることと予想できる。
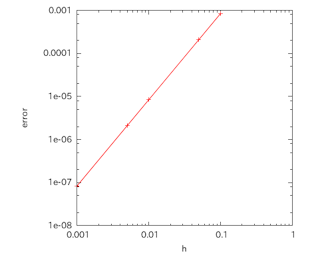
さらにa=0とし、hを変化させ、
と近似したときの誤差を求めると右図のようになる。このときの直線（緑色の直線）の勾配は２であり、この近似式の誤差はhの２次オーダーであることがわかる。
f(x)がxの２次関数であるとき、
となるので、
が成立する。したがって、この近似式は２次の精度を持っている。
要するに、
という記号は、n次の精度で、誤差の程度は
のオーダーであり、hを1/10にすると、誤差は
になるということを表していると考えることができる。
の近似式を求めるために、（５）と（５’）の辺々を加えると、
したがって、
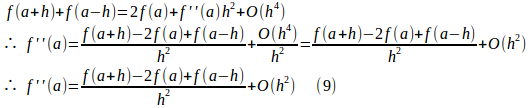
という近似式は、２次の精度をもっており、誤差はh²程度ということになる。
この直線の傾きは２であり、誤差がhの２次のオーダーであることが確かめられる。
