数値計算の誤差：打ち切り誤差と丸め誤差

数値計算の誤差：打ち切り誤差と丸め誤差

 

f(x)は何回でも微分可能な関数とする。

このとき、f(a+h)はx=aにおいて次のようにテーラー展開が可能である。

有限項で打ち切れば、

は剰余項であり、有限項で打ち切ったときの誤差に相当する。

 

最も簡単なa=0のときを考えてみる。

かりに

という関数があるとする、

だから、これをx=0でテーラー展開（マクローリン展開）すると、

と一致する。

 

有限な多項式で表される関数ならば、上の例のように第n次以下の導関数を求めることによってその係数を求めることができる。しかし、テーラー展開（マクローリン展開）が指数関数のように、

と無限級数になる場合、これを無限に計算することはできないので、適当な次数nで打ち切って計算をしなければならない。

たとえば、３次の以上の項を落とせば、

そして、その誤差、打ち切り誤差O(x³)は

と評価されるであろう。

 

この他に、有限桁の数しか扱えないコンピュータの計算誤差には、丸め誤差と呼ばれるものがある。

たとえば、１０進数の0.1は２進数で書くと

という無限小数、循環小数になってしまう。

したがって二進数の小数点８桁で打ち切ると0.00011001（二進数）となる。この0.00011001（二進数）を十進数に直すと0.09765625（十進数）となるので、十進数で0.00234375という誤差が発生することになる。

このような計算機特有の誤差を丸め誤差という。

 

この他に桁落ちというものがある。

例えば、

という計算を考える。

いま仮に１０進数で８桁（浮動小数）しか精度を有さない計算機があるとする。

そして、これを使って上の計算を行おうとすると、

最初８桁あった有効精度が５桁に落ちてしまう。

このように、近い数同士の引き算をする場合、計算の精度が落ちてしまうことがある。

このような現象を桁落ちという。

しかし、次のように計算すると、

と精度が保たれる。

今のコンピュータ、とりわけ電卓は賢いので、どのように計算しても同じ計算結果を出すが・・・。

 

わかりやすいように１０進数を使って説明しているけれど、正確な議論をする場合、コンピュータは２進数で計算をしているので、２進数を使って議論をしなければならない。

この点は留意して欲しい。

 

この他に、たとえば、十進数で３桁しか精度を持たないコンピュータの場合、1000+1を計算すると、

となってしまう。

このように、大きな数（？）と小さな数（？）の足し算でも情報が落ちる情報落ちという現象が起きる。

整数３桁しか扱えないコンピュータなどあるものかと思うかもしれないけれど、かつて存在した８ビットのパソコンで扱える整数は、特別な処理を施さないかぎり、±の符合を有する整数の場合−128〜+127、符合を有さない整数の場合0〜255だ。

という計算をするためには、符号なしの整数の場合、最低でも10ビット必要でそれほど荒唐無稽な話ではないのである。

上の有効精度３桁というのは極端な例だが、Fortranで1000000+0.001を単精度で計算させると、次のような計算結果が得られる。

 

 

 

0.001という情報が落ちてしまっている。

つまり、情報落ちが発生している。

また、先に話したように、0.001は、一旦、２進数に変換されるので、これを１０進数に戻すときに1.00000005×10⁻³となっており、丸め誤差が発生していることもわかると思う。

 

このように、コンピュータで計算する場合、打ち切り誤差以外の様々な誤差が計算に混入する。そして、時に、計算途中で誤差が誤差を次々と生み出し、それが雪だるま式に膨れ上がり、この誤差の蓄積のために、とんでもない計算結果が得られるのであった。

 

タグ：数値解析

［境界要素法プログラムを設計する（基本のGauss掃き出し法）］

［境界要素法プログラムを設計する（基本のGauss掃き出し法）］

 

１．Gauss掃き出し法の標準構成

　前回の[外部手続き]の最後に、

    REM Gauss掃き出し法 **********************************************
    External Sub Gauss_0(A, z, n, Zero_Order, Return_Code)
      REM まだ何にもしない
    End Sub

という、よくわからんものがくっついてたはずです(^^)。今回はこの中身をつくろうという話です。Gauss掃き出し法は連立一次方程式を解く、標準解法です。なので別に境界要素法でなくても良いのですが(^^;)。

　Gauss_0の引数Aは、解くべき連立一次方程式の係数マトリックスを表す配列，zはGauss_0が呼ばれた時は連立一次方程式の既知ベクトル（配列）で、Gauss_0の処理が終わると解ベクトルになっています。nは未知数の数，Zero_Orderは後述するピボット選択で使用する0判定オーダーを表す整数，Return_Codeは計算終了状態をGauss_0の外部へ伝えるために用意した引数です。

 

　標準解法なので、数値計算業界（？）の業界標準みたいな構成があります。こういう構成です。

 

    External Sub Gauss_0(A, z, n, Zero_Order, Return_Code)
      External Sub Scaling
      External Sub Foward_Eliminate
      External Sub Back_Sub

      REM ｽｹｰﾘﾝｸﾞ
      Call Scaling(A, z, n, Return_Code)

      If Return_Code <> 0 Then
        Return
      End If

      REM 前進消去
      Call Foward_Eliminate(A, z, n, Zero_Order, Return_Code)

      If Return_Code <> 0 Then
        Return
      End If

      REM 後退代入
      Call Back_Sub(A, z, n)
    End Sub

 

　とりあえず、If Return_Code <> 0 ThenのIfブロックはおいといて、REM文の後のサブルーティン呼び出しに注目です。呼ばれるサブルーティンは、スケーリング(Scaling)，前進消去（Foward Elimination），後退代入（Back Substitution）を行います。このうち前進消去と後退代入の意味がわからない人は、

ネコ先生の記事を読もう！。

 

２．スケーリング

　スケーリングは桁落ち誤差対策です。連立一次方程式の係数マトリックスを表す配列Aは、ふつう倍精度浮動小数点実数で宣言されますが、倍精度浮動小数点実数型の公称有効数字は16桁と決まっています（国際規格）。以下は極端な例ですが、次の2元連立一次方程式を考えます。

　　

　上記を解くと、(2)－(1)で、

　　

　(2')より、

　　

なので、(3)を(1)に代入し、

　　

となります。(3)，(4)より厳密解は、ほとんどx＝2，y＝1である事がわかります。数値計算には必ず数値誤差が憑きもの（？(^^;)）です。なので例え数値誤差が憑いたとしても、x＝2，y＝1程度の近似解は出るようにしたい訳です。

　同じ事をコンピューターにやらせると、既に(2')の段階でコンピューター内部では-(1+10²⁰) → -10²⁰，1-10²⁰ → -10²⁰という現象が起きてしまいます。有効数字が16桁しかないからです。

　すると(3)でy＝1となり、それを(1)に代入するとx＝0となって全くお話になりません。何故ならx＝0，y＝1を(2)に代入すると、誤差がありとしても想定外の、-1＝1という不当過ぎるな結果になるからです。

　一方、

　　

としてもOKなはずです。(1')は(1)の両辺を10²⁰で割っただけのもの。ここで(2)－(1')をやるために、(1')のxの係数を1にしようとして、(1')を10²⁰倍したら馬鹿です。(1)と(2)の状態に戻るので。(1')－10^-20×(2)を試してみましょう。下から上を引いた方が考えやすいので行交換を行い、

　　

として(1')－10^-20×(2)を行うと、

　　

　(1")より、

　　

 

と(3)と同じものが得られますが、これを(2)に代入すれば、x＝2が得られます。

　だまされたような気持ちですか？(^^)。でもこのトリックは正しいんです。理由はなんでしょう？。連立方程式の「構造」に注目します。(1)と(1')を比べると、条件(1')ではxの寄与は非常に小さいとわかります。無視してもいいくらいです。無視するとy＝1です。それを(2)に代入しx＝2。(1)と(1')は同じ条件のはずなのに・・・。

 

　以上を強引にまとめると、こうなります。

　大きすぎる数値で桁落ちが起こるより、非常に小さい数値で桁落ちが起こった方がましだ！。

　そして桁落ちは必ず起こる！。

 

　理由は連立方程式の中で微小な係数しか持たない部分は、最初から無視しても構造的に被害小だからです。いいかえれば、ちゃんとした近似構造を解いた。

　しかし連立方程式の各条件は、何倍しても理屈の上では同じ条件。本当は寄与が少ない部分も、生の数値ではそう見えないかも知れない。よって寄与が少ないと見分けるためには、連立方程式の各行の数値桁数を揃えればいい、という話になります。そのために、連立方程式の各行を各行の絶対値最大成分の値で割り、各行の最大係数を1に揃える作業を、スケーリングと言います（←　一種のスケール規模問題です）。

　スケーリングを行うと、連立方程式の数値的安定性は格段に向上します。でも数値誤差は憑き物(^^;)。弊害もあります。ほとんど特異な連立方程式（解けちゃいけない）が、安定に解けてとんでもない答えが出る場合もあります。そして人間は馬鹿だから、その答えを信じます(^^;)。

 

　ところで(1')(2)を(2)(1')にしたような行交換を、機械は自動で出来るものでしょうか？。それは次のピボット選択と関連します。

　ところで桁落ち誤差の意味がわからない人は、ネコ先生の記事を読もう！。

 

 

 

３．ピボット選択

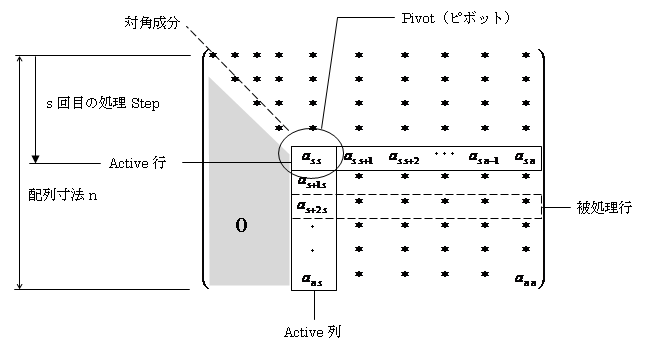
　ピボット選択は基本的に丸め誤差対策です。掃き出し中の連立一次方程式の係数配列は、概ね下図のようになります。灰色の部分は掃き出し完了ブロックで、成分は全て0です。Active行，Active列に囲われた部分が、これからs回目の掃き出しを行おうという、未処理ブロックになります。Active行，Active列の交点を、特にピボット（Pivot：枢軸）と言います。

 

　掃き出し処理は、Active列のs+1行～n行成分を0にすれば完了です。そのためにまず、Active行をピボットa_ssで割り、被処理行の頭の値a_{s+2 s}などをActive行にかけて、非処理行から引きます。「/」を使う時には、常に割る数が0でないかどうかのチェックが必要です。

　a_ssがたまたま0という事はあり得ます。でもActive列の中には非零成分がたぶんあります。そこでActive列のs行～n行を検索し、最初に見つかった0でないa_ksを持つ行をActive行（s行）と交換し、k行目をActive行とすればOKです。もしActive列に非零成分がなければ、特異行列です。答えがでちゃいけません。そこで処理を中止します。

 

 

　でも数値誤差は憑き物。本当は0なんだけど0に近いが0になってない数値はきっと、Active列にもごろごろしてます(^^;)。どれくらい小さければ0とみなすか？。要するに閾値Epsはどれくらいか？。これは問題のスケール規模で決まります。

　係数配列の数値は平均的に非常に大きい場合もあるし、逆もありえます。両方で同じEpsを使っては計算精度なんか保証されません。でもスケーリングしたのでした。各行の最大成分は初期状態で必ず1です。スケール規模は「1」です。「1」を基準にEpsを決定できます(^^)。ここで引数Zero_Order登場です。Active列の非零成分検索で、絶対値が　Eps＝1.0 * 10^(-Zero_Order)　未満のものは0とみなします。自分は経験的にZero_Order＝8を使います。

 

　でも非零という条件だけでいいのでしょうか？。係数配列は初期状態においてすら、すでに各数値には丸め誤差δが含まれます。コンピューターの数値には、有限の有効桁数しかないからです。コンピューターの中の方程式とは、要するに最初から近似方程式なんですよ。数値誤差は数値計算の憑き物！(^^;)。

　真の値がa_ij＋δならば、それをピボットa_ssで割る事により、丸め誤差の影響はδ/a_ssになります。小さすぎるa_ssで割ると、丸め誤差の影響は拡大します。もう一つ困るのはa_ssが微小だと、スケーリングのところでやった(1')を、わざわざ(1)に戻すような事まで起きる可能性がある事です。せっかくスケーリングしたのに。

 

　なので、Active列の絶対値最大成分を持つ行をActive行と交換します。これがピボット選択（行ピボット選択）です。あれっ、(1')と(2)の行交換が自動で出来ちゃった・・・(^^)。

 

　スケーリングとピボット選択をセットで使うと、概ね6桁くらいの有効数字を数値誤差の影響から救えます。10^6＝1,000,000なので、馬鹿にならない数字です。

　ところで丸め誤差の意味がわからない人は、ネコ先生の記事を読もう！。

 

REM ｽｹｰﾘﾝｸﾞ
External Sub Scaling(A, z, n, Return_Code)

  For i = 1 to n
    Ma = 0
    jj = 0

    REM 行の絶対値最大成分を検索
    For j = 1 to n
      h = Abs(A(i, j))

      If Ma < h Then
        Ma = h
        jj = j
      End If

    Next j

    REM 行が0だったら処理中止
    If Ma = 0 Then
      Return_Code = 1
      Return
    End if

    REM 絶対値最大成分で行を割り規格化
    h = A(i, jj)
    z(i) = z(i) / h

    For j = 1 to n
      A(i, j) = A(i, j) / h
    Next j

  Next i

  Return_Code = 0
End Sub

 

REM 前進消去
External Sub Foward_Eliminate(A, z, n, Zero_Order, Return_Code)

  REM 0判定値セット
  Eps = 10^(- Zero_Order)

  For i = 1 to n

    REM Pivot検索
    Ma = 0
    ii = i

    For k = i to n
      h = Abs(A(k, i))

      If Ma < h Then
        Ma = h
        ii = k
      End If

    Next k

    REM Pivot候補がEps未満だったら処理中止
    If Ma < Eps Then
      Return_Code = 2
      Return
    End if

    REM 行選択Pivot
    If ii <> i Then
      P1 = z(i)
      P2 = z(ii)
      z(i) = P2
      z(ii) = P1

      For j = i to n
        P1 = A(i, j)
        P2 = A(ii, j)
        A(i, j) = P2
        A(ii, j) = P1
      Next j

    REM 掃き出し処理
    h = A(i, i)  REM Pivotｾｯﾄ
    z(i) = z(i) / h  REM 既知ﾍﾞｸﾄﾙのActive行を規格化

    For j = i + 1 to n  REM 係数配列のActive行を規格化
      A(i, j) = A(i, j) / h
    Next j

    For k = i + 1 to n  REM 掃き出し
      h = A(k, i)  REM 非処理行の頭をｾｯﾄ

      If h <> 0 Then  REM Fillin Skip
        z(k) = z(k) - h * z(i)  REM 既知ﾍﾞｸﾄﾙの掃き出し

        For j = i + 1 to n  REM 係数配列の被処理行を掃き出し
          A(k, j) = A(k, j) - h * A(i, j)
        Next j

      End If

    Next k

  Next i

  Return_Code = 0
End Sub


REM 後退代入
External Sub Back_Sub(A, z, n)

  For i = n to 1 Skip -1
    h = 0

    For j = n to i + 1 Skip -1
      h = h - A(i, j) * z(j)
    Next j

    z(i) = h
  Next i

End Sub

 

(執筆　ddt²さん）

タグ：境界要素法 数値解析