放物型偏微分方程式の解法 ルンゲ・クッタ法

放物型偏微分方程式の解法　ルンゲ・クッタ法

 

次の熱伝導方程式

　　

の右辺を差分法を用いて次のよう

　　

と近似し、

とおくと、ルンゲ・クッタ法を用いて、（１）式の近似解を求めることができる。

すなわち、

　　

 

例によって、（２）を用いて、次の問題を解くと、右のグラフのようになる。

 

問題

　　

を、初期条件

　　

境界条件

　　

のもとで、Δt=1、Δx=1として解け。

 

 

 

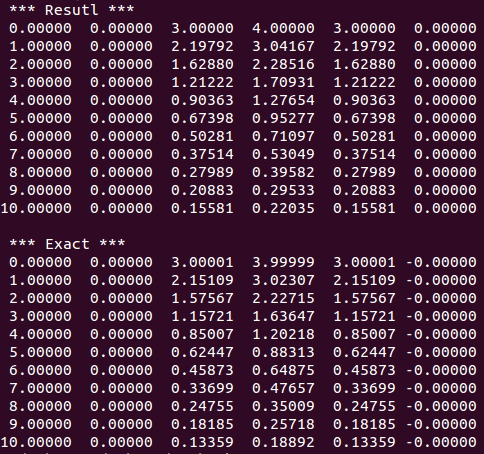
Δt=1、Δx=1という粗い計算でも、良好な計算結果が得られていることが分かる。

 

Δt=0.1、Δx=0.4とすると、さらに良好な結果が得られ、厳密解との差はほとんど認められなくなる。

 

 

なのですが、ルンゲ・クッタ法も陽解法の一種なので、

　　

のとき数値解が振動することがあるので、ルンゲ・クッタ法を用いて熱伝導方程式を解くとき、

　　

になるようにΔt、Δxを取ったほうがよい。

このことを示すために、Δt=0.36、Δx=0.5のとき、すなわち、

として計算すると、４０ステップのt=14.4の前後で振動を始め、t=18ではさらに激しく振動する。

計算に使用したプログラムは次の通り。

 

 

! ルンゲ・クッタ法による解法
parameter (nt=20, nx=10)
real t(0:nx, 0:nt)
real dk(4,0:nx)
real l,kappa

l=4.; kappa=0.5
dt=0.2
dx = l/nx
dx2=dx*dx
c=kappa/dx2

dk= 0
   
! 初期化
do i=0, nx
    do j=0,nt
        t(i,j)=0.
    end do
end do

! 初期条件
do i=0,nx
    x=i*dx
    t(i,0)=x*(l-x)
end do

! 境界条件
do j=0,nt
    t(0,j)=0.
    t(nx,j)=0.
end do

! Runge-Kutta Method
do j=1,nt
    do i=1,nx-1
        dk(1,i) = dt*f(t(i-1,j-1),t(i,j-1),t(i+1,j-1),c)
    end do
   
    do k=2,3
        do i=1,nx-1
            dk(k,i)=dt*f(t(i-1,j-1)+dk(k-1,i-1)/2,t(i,j-1)+dk(k-1,i)/2,t(i+1,j-1)+dk(k-1,i+1)/2,c)
        end do
    end do

    do i=1,nx-1
        dk(4,i)=dt*f(t(i-1,j-1)+dk(3,i-1),t(i,j-1)+dk(3,i),t(i+1,j-1)+dk(3,i+1),c)
    end do
   
    do i=1, nx-1
        t(i,j) = t(i,j-1)+(dk(1,i)+2.*dk(2,i)+2.*dk(3,i)+dk(4,i))/6
    end do
end do

write(6,*) '*** Resutl ***'
do j=0,nt
    write(6,100) j*dt,(t(i,j),i=0,nx)
end do

write(*,*)
write(6,*) '*** Exact ***'
do j=0,nt
    write(6,100) j*dt,(exact(i*dx,j*dt),i=0,nx)
end do

100 format(12(f8.5,1x))

end

function f(x,y,z,c)
f=c*(x-2.*y+z)
end

! 厳密解
function exact(x,t)
pi = acos(-1.0)
s=0.
do i=1,30
    s=s+128/((2*i-1)**3*pi**3)*exp(-(2*i-1)**2*pi**2/32*t)*sin((2*i-1)*pi/4*x)
end do
exact = s
end

タグ：数値解析 微分積分 微分方程式