第33回 曲線座標 [ネコ騙し数学]
第33回 曲線座標
直交座標x、y、zの関数
u=F(x,y,z), v=G(x,y,z), w=H(x,y,z) ①
x=f(u,v,w), y=g(u,v,w), z=h(u,v,w)
が得られる。そして、x,y,zの値の一組にはu,v,wの値の一組が対応し、逆にu,v,wの値の一組に対してx,y,zの値の一組が対応するから、u,v,wの組を座標と考えることができ、これを曲線座標という。いま仮にc₁を定数とし、u=c₁とすると、F(x,y,z)=c₁は一つの曲面をえがく。そして、c₁を変化させれば、曲面群が得られる。同様に、v=c₂、w=c₃とすれば、2種類の曲面群が得られ、この3つの曲面群を座標曲面という。
たとえば、
そう言った話。
2つの座標曲面v=c₂とw=c₃の交わりは曲線でこれをu曲線という。u曲線に沿っては、v=c₂、w=c₃なので、vとwは一定で、uの値だけが変化する。同様にして、w=c₃とu=c₁の交わりをv曲線、u=c₁とv=c₂の交わりをw曲線という。
任意の点をPとすれば、Pを通るu曲線、v曲線、w曲線が一つずつ存在する。Pを始点とし、u曲線に接し、uの増加する向きに向かう単位ベクトルをuとする。同様に、v曲線、w曲線に接し、u、vの増加する向きに向かう単位ベクトルをv、wとする。
そうすると、下の図のような座標系が得られる。
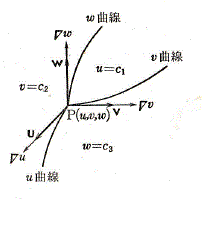
で、各点で3つのベクトル、u、v、wが互いに直交するものとする。この時、このとき、u、v、wを直交曲線座標という。なお、u、v、wは右手系をなすものとする。
点(x,y,z)の位置ベクトルをrとすれば、線元素dsは
![]()
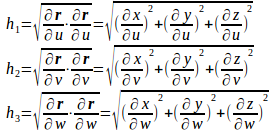
したがって、u曲線、v曲線,w曲線の弧長をそれぞれs₁、s₂、s₃とすると
直交曲線座標では、uは曲面u=c₁に垂直で、uの増加する向きに向かう単位ベクトルだから
ベクトルAを、その始点Pにおけるu、v、wの方向に分解して、
であるとする。このとき、をそれぞれ曲線座標u、v、wに関するAの成分、または、Aのu成分、v成分、w成分という。
このu、v、wは直交座標のi、j、kとは異なり、始点Pの位置によって向きが変わるにゃ。
例として、3次元の極座標をあげることにするにゃ。
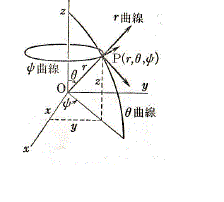




コメント 0