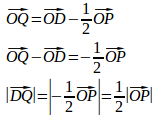微分係数と微分可能性の問題

微分係数と微分可能性の問題

問題１　関数f(x)のx=aにおける微分係数f'(a)が存在するとき、つぎの極限値をa、f(a)、f'(a)を用いて表せ。

　　

【解】

（１）

　　

h→0のとき

　　

よって、
　　

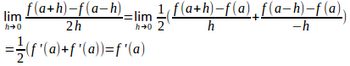
（２）　x=a+hとすると、h=x−a。

よって、x→aのとき、h→0。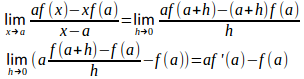
　　

（解答終わり）

（２）は、次のように解くこともできる。

【別解】

　　

よって、

　　

（別解終わり）

 

問題２　関数f(x)が任意の実数x,yに対して常に

　　

を満足しているとき、次の問いに答えよ。

（１）　f(0)を求めよ。

（２）　f'(0)=0として、x=aにおける微分係数f'(a)を求めよ。

【解】

（１）

　　

にx=y=0を代入すると、

　　

（２）

　　

よって、

　　

（解答終わり）

（２）より、問題２の関数は、x=0で微分可能ならば、任意の点aで微分可能なことが分かる。

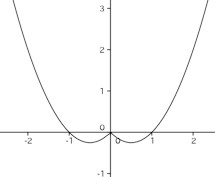
また、（２）より、f(x)=x²である。

問題３　次の関数の連続性と微分可能性について論ぜよ。

　　

【解】

（１）

　　

よって、 となり、f(x)はx=0で連続である。

x≠0のとき

　　

x→0のとき、sin(1/x)は振動し収束しないので、f(x)はx=0で微分可能でない。

（２）

　　

よって、g(x)はx=0で微分可能である。

x=0で微分可能だから、g(x)はx=0で連続である。

（解答終わり）

定理

f(x)がx=aで微分可能ならば、x=aで連続である。

【略称】

　　

よって、x=aで微分可能ならば、x=aで連続である。

タグ：微分積分

平均変化率と微分係数

平均変化率と微分係数

§１　平均変化率

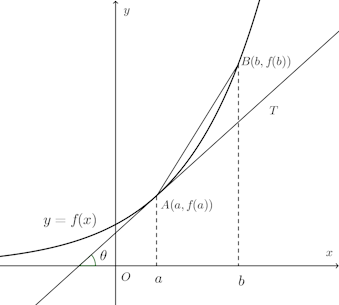
関数y=f(x)がx=aからx=bまで変化すると、それに応じてyもf(a)からf(b)に変化する。

その値の変化は

　　xの変化（増分）　b−a

　　yの変化（増分）　f(b)−f(a)

であり、変化の割合は

　　

である。、これをy=f(x)のx=aからx=bまでの平均変化率という。

グラフでは直線ABの傾きをあらわす。

§２　微分係数

関数y=f(x)のx=aにおける微分係数は

　　

あるいは、

　　

である。

グラフでは、点(a,f(a))における接線ATの傾きをあらわす。

また、接線ATがx軸となす角をθとすると、

　　

§３　微分可能

関数y=f(x)がx=aで微分係数をもつことは極限

　　

が存在することである。このとき、f(x)はx=aで微分可能であるという。

　　

を右側微分係数、

　　

を右側微分係数という。

f(x)がx=aにおいて微分可能である必要十分条件は、

　　

が成り立つことである。

§４　問題

問題１　定義に基づいて、x=aにおける微分係数f'(a)を求めよ。

　　

【解】

（１）

　　

（２）

　　

（３）

　　

問題２　関数y=f(x)=x³−4xのx=aにおける微分係数が区間[−1,1]における平均変化率に等しくなるようなaの値を求めよ。

【解】

　　

[−1,1]における平均変化率は

　　

よって、

　　

問題３

（１）　はx=0で微分可能か

（２）　次の関数f(x)はx=1で微分可能か

　　

【解】

（１）

　　

h>0のとき、|h|=hだから

　　

h<0のとき、|h}=−hだから

　　

したがって、微分可能ではない。

（２）　h<0のとき

　　

h>0のとき
　　

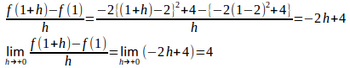
よって、微分可能である。

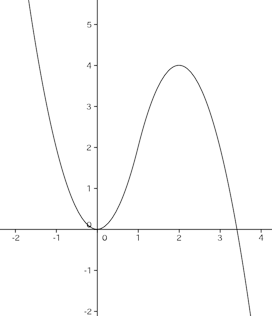
（解答終わり）

タグ：微分積分

微分積分 除去可能な不連続

微分積分　除去可能な不連続

f(x)はx=a以外で連続で、x=aにおいて定まった値を持たず不連続であるが、

　　

が有限確定であるとする。

このとき、x=aにおけるf(x)の値をf(x)=bと定めると、f(x)は連続になる。

例

　　

この関数は、x=2で0/0で定まった値を持たず不連続。

しかし、x=2におけるf(x)の値を

　　

と定義し、

　　

とすると、f(x)はx=2で連続になる。

 

問題１

　　

は、f(0)をどのように定めたら、連続になるか。

【解】

x≠0で

　　

よって、

　　

また

　　

ハサミ打ちの定理より

　　

である。

したがって、f(0)=0に定めればよい。

（解答終わり）

ハサミ打ちの定理

f(x)≦g(x)≦h(x)かつ

ならば

である。

問題２

　　

がxのすべての値に対して連続であるようにa、bの値を定めよ。

【解】

|x|>1のとき

　　

|x|<1のとき

　　

x=1のとき

　　

x=−1のとき

　　

x=1で連続であるためには

　　

x=−1で連続であるためには

　　

でなければならない。

①と②よりa=0、b=1である。

【解答終わり】

極限の計算で、

　　

を使っている。

さらに、

　　

を使っている。

タグ：微分積分

数列とは何か

数列とは何か

数列とは何か？

数列の定義は意外に難しいらしく、ネットでいくつかその定義を調べてみたところ、

数列とは、ある規則に従ってならべられた数の列のこと

くらいの定義しかないようだ。

名著とされる高木貞治の『解析概論』では、次のように数列が定義されている。

のように、無数の数を一定の順序でならべたものを数列という。その項は自然数の範囲内において変動する変数nの’函数’である。この函数が確定したときは、数列をと書く。

まだまだ文学的な表現で、定義としては不十分のように思う。

その点、とある本に書いてある数列の定義は実に明快だ。

自然数の全体をNであらわす。

NからRへの写像

を実数列あるいは単に数列といい、あるいは単にとあらわす。これは実数をとならべたものである。

なお、ここで、Rは実数のことである。

この定義によれば、自然数Nから実数Rへの写像、関数を特に数列と呼び、区別しているようである。

ではあるが、これではあまりに抽象的でわかりづらいと思うので、高校数学風の次の定義を紹介する。

ある規則によって何番目の数が何であるかが定められる数の列を数列といい、数列を作っている各数を項という。

という数列があるとき、を初項、を第２項、……、を第n項という。

数列をまたは単にとあらわす。

数列には、無限に続くもの（無限数列）と有限で終わるもの（有限数列）がある。有限数列においては、項の個数を項数、最後の項を末項という。

がnの式の形で書かれ、それによって数列が一般的に示されるとき、を一般項という。

例

　　

という数列があったとき、一般項は

　　

である。

問題　次の数列の空所を満たし、その第n項を求めよ。

　　

【解】

　　

（解答終わり）

どうやって、この関係を見つけたって？

勘(^^ゞ

（１）は、nが1増えるごとに、1/2減っているようなので

　　

らしい。

（２）は勘だにゃ。

（３）は、nが１増えると、3/2倍になっている.

（４）は、分子が1, 3, △, 7だから、2n-1と推測できる。分母は2, 4, ◯, 16だからと推測できる。

したがって、

　　

であろう。

実は、この手の問題は、一般項の式がひと通りに決まらない。複雑な式で□の部分を予想でき、その推測式によって□の値が変わる。

例えば、（２）、（４）はラグランジュ補間を使って

　　

とnの２次式の形で一般項を求めることができる。

（３）は、ラグランジュ補間を使うと

　　
と２次式ので一般項を求めることができるのだ。

ラグランジュ補間

ラグランジュ補間を使うと、というn+1個の相異なる点があるとき、このすべての点を通るn次式を求めることができる。

の３点であるとき、２次のラグランジュ補間の式は

　　

である。
上の補間式に使うと

　　

になることを確かめて欲しい。

タグ：数列

ベクトル 直線の方程式（平面の場合）

ベクトル　直線の方程式（平面の場合）

§１　直線の方程式

点Aを通り、方向がである直線lがあるとする。

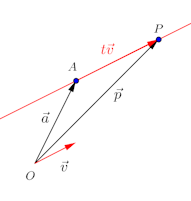
点Pが直線l上にあるので、

　　

となる実数tが存在する。

点Aと点Pの位置ベクトルをそれぞれ

　　

とすると、

　　

より

　　

となる。

ここで、tはすべての実数値をとる変数、媒介変数である。

次に、直線l上に２点A、Bがあり、その位置ベクトルをとする。

直線lはに平行なので、

　　

と考え、上式に代入すると

　　

この結果をまとめると、次のようになる。

１．　点を通り、方向の直線の方程式

　　

２。　２点を通る直線の方程式

　　

s+t=1とすると、上の式は次のように書き換えることができる。

　　

§２　問題

問題１　２点A(−2,3)、B(2,−4)を通る直線上の任意の点の座標を、媒介変数tを使ってあらわせ。

【解】

　　

さらに、直線上の任意の点Pの位置ベクトルを

　　

とする。

　　

したがって、

　　

（解答終わり）

　　

を使って計算してもいいけれど、上のように解いたほうが、計算は楽でしょう。

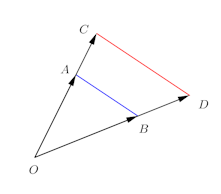
問題２　平面上に異なる３点A、B、Cがある。s、tは、s≧0、t≧0であるような実数値をとる変数で

　　

とする。

（１）　s+t=1のとき、Pの軌跡を求めよ。

（２）　s+t=k（kは正の定数）のとき、Pの軌跡を求めよ。

（３）　s+t≦1のとき、Pの存在範囲を求めよ。

【解】

（１）　s+t=1よりs=1−t。

また、s≧0とt≧0より、0≦t≦1。

　　

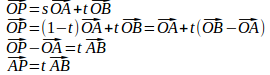
t=0のときP=A、t=1のときP=B。また、点Pは線分AB上を動くので、点Pの軌跡は線分AB（両端を含む）である。

（２）　l=sk、m=tkとおくと、l≧0、m≧0で

　　

さらに、

　　

とおくと、

　　

（１）より、Pの軌跡は線分CDであり、よって、Pの軌跡は原点を中心にABをk倍した線分CDである。

（３）　s+t=kとおくと0≦k≦1。

よって、点Pの存在範囲は、△OABの内部とその周である。

（解答終わり）

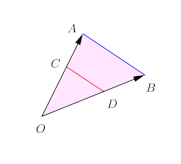
問題３　１直線上にない３点A、B、Cがあって、とする。∠AOBの２等分線が直線ABと交わる点をPとするとき、次のことを示せ。

　　

【解】

　　

とする。

（１）　Pは直線AB上にあるので

　　

またPは∠AOBの２等分線上にあるので

　　

よって
　　

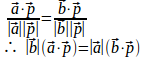
内積を計算すると

　　

これを代入すると、

　　

∠AOB≠0だから、

よって

　　

s+t=1と連立して解くと、
　　

（２）

　　

よって、

　　

である。

タグ：ベクトル

ベクトル 空間図形への応用

ベクトル　空間図形への応用

問題１　正四面体ABCDの辺AB、BC、CD、DAの中点をそれぞれP、Q、R、Sとするとき、次の問いに答えよ。

（１）　AB⊥CD、AC⊥BD、AD⊥BC

（２）　PR⊥AB、PR⊥CD

【解】

　　
とする。

正四面体だからAB=AC=AD。

正四面体の１辺の長さをaとすると、

　　

また、△ABC、△ABD、△ACDは正三角形だから、∠BAC=∠BAD=∠CAD=60°。

　　

（１）

　　

同様に、AC⊥BD、AD⊥BC

（２）　とする。

　　

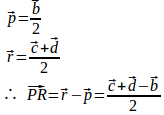
よって、

　　

また、

　　

よって、

　　

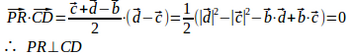
問題２　立方体の３つの辺をOA、OB、OCとし、同一の平面上にない頂点をDとすると、ODは△ABCの平面に垂直であることを示せ。

【解】

立方体の１辺の長さをaとし、O(0,0,0)、A(a,0,0)、B(0,a,0)、C(0,0,a)とする。さすれば、D(a,a,a)。

　　

そうすると、

　　

よって、

　　

だから、ODと△ABCの平面は垂直である。

（解答終わり）

座標を導入せず、次のように解いてもいい。

【別解】

　　

立方体だから

　　

また、

　　

だから、

　　

よって、OD⊥AB、OD⊥AC。

したがって、ODと△ABCの平面に垂直である。

（解答終わり）

問題３　空間の３点A(2,0,0)、B(0,2,0)、C(0,0,1）がある。

（１）　△ABCの面積を求めよ。

（２）　原点Oから△ABCに垂線OHをひくとき、の向きの単位ベクトルを求めよ。

（３）　△ABCの平面と△AOCのなす角の余弦を求めよ。

【解】

（１）
　　

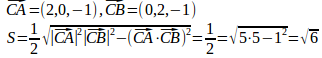
（２）
　　
とする。

単位ベクトルだから

　　

また、OH⊥CA、OH⊥CBだから

　　

よって、

　　

x≧0、y≧0、z≧0だから、
　　

 

（３）　△ABCの平面の単位垂直ベクトルは、△AOCの単位垂直ベクトルをとすると

　　

この２つの平面のなす角をθとすると

　　

タグ：ベクトル

ベクトル 演習問題

ベクトル　演習問題

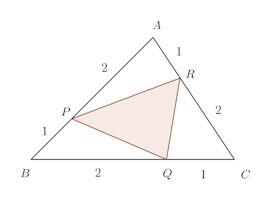
問題１　△ABCと△PQRの間に、次の関係がある。

　　

△ABCと△PQRの面積比を求めよ。

【解】

　　

とする。

　　

よって、点PはABを2:1に内分する点。

同様に、QはBCを、RはCAを2:1に内分する。

よって、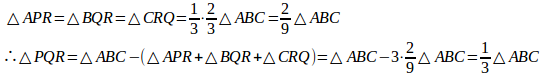

　　

（解答終わり）

問題２　ベクトルがあって、の間に

　　

の関係がある。

（１）　の内積をkを用いて表せ。

（２）　内積の最小値、およびそのときののなす角θ（0≦θ≦180°）を求めよ。

【解】

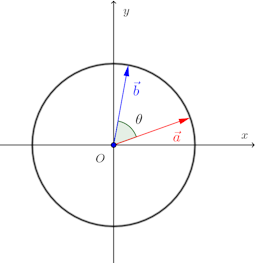
（１）　だから、。

また、

　　

（２）

　　

相加平均≧相乗平均より

　　

よって、

　　

したがって、内積の最小値は1/2。

　　

（解答終わり）

 

問題３　円Oに内接する△ABCがある。動点Pが円O上を動くとき、

　　

を満たす点Qの軌跡は、△ABCの各辺の中点を通る円であることを示せ。

【解】

　　

とする。

　　

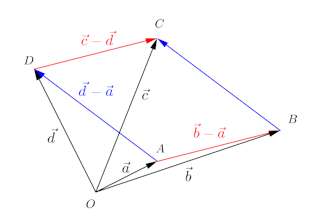
△ABCの外接円の半径をRとすると、は△ABCの外接円の半径Rであり、点QはDを中心とする半径R/2の円周上の点である。

また、

　　

より、点Aと点Pが一致するとき、つまり、

　　

のとき

　　

で、点Qは辺BCの中点と一致し、したがって、点QはBCの中点を通過する。

同様に、点Pが点Bに一致するときはCAの中点、点Cと一致するときはABの中点を通る。

以上のことより、点Qの軌跡は、△ABCの各辺の中点を通る円である。

（解答終わり）

△ABCの重心をGとすると、

　　

だから、

　　

である。

タグ：ベクトル

ベクトル ベクトルの図形への応用２

ベクトル　ベクトルの図形への応用２

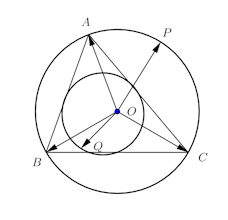
問題１　決まった平行四辺形ABCDがある。任意の点Pに対して、

　　

が一定であることを証明せよ。

【証明】

　　
とする。

四角形ABCDは平行四辺形だから

　　

よって、

　　

したがって、この値は、任意の点Pによらず、一定である。
（証明終わり）

この問題の結果を使うと、次の問題を簡単に解くことができる。

問題２　、を満たすベクトルを位置ベクトルとする４点A、B、C、Dはどんな位置関係にあるか。

【解】

　　

よって四角形ABCDは平行四辺形。

として問題１の結果に代入すると

　　

よって、AB⊥AD。

以上のことから、四角形ABCDは長方形。

（解答終わり）

そして、平行四辺形の面積を与える公式の証明。

問題３　平面上の２つのベクトルを隣り合った２辺とする平行四辺形の面積をSとするとき、

（１）　であることを証明せよ。

（２）　のとき、Sを求めよ。

【解】

（１）　平行四辺形の面積Sは、∠AOB=θとすると

　　

内積の定義から

　　

よって

　　

（２）　（１）より

　　

で、S≧0だから

　　

（解答終わり）

問題２の（１）より

平面上の２つのベクトルを隣り合った２辺とする平行四辺形の面積をSは

　　

平面上の２つのベクトルを隣り合った２辺とする三角形の面積は

　　

問題４　平面上で、３点A(1,1)、B(2,3)、C(4,−1)を頂点とする三角形の面積を求めよ。

【解】

　　

（解答終わり）

 

タグ：ベクトル

関数の連続

関数の連続

関数の連続について述べる前に、関数の極限についての補足説明をする。

§１　有限確定について

xが限りなくaに近づくとき、関数f(x)がある一つの実数bに限りなく近づくとき、このことを

　　

と表し、bを関数f(x)のaにおける極限、または、極限値という。

そして、このとき、は有限確定という。

また、またはであるときは、は確定であるという。

有限確定ではなく、確定である代表的な例は

　　

がある。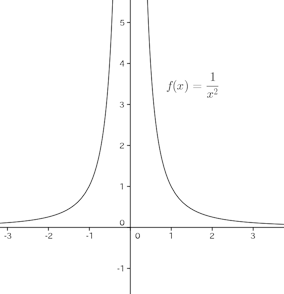



+∞や−∞は、数、実数でないので、これを極限、極限値と考えていいのかどうかという問題はあるけれど・・・。

関数f(x)の極限が存在しない例代表的な例としては、

　　

がある。

この場合、x=0における左側極限、右側極限は次のようになる。

　　

この他に、

　　

も、x=0における極限は存在しない。

たとえば、
　　

として、xを0に近づけてゆくとき、

　　

だから、この近づき方では

　　

になる。

しかし、

　　

といったように、xの0への近づき方によって、値が変わってしまう。

一つの値に定まらないので、この場合もx=0における極限は存在しない。

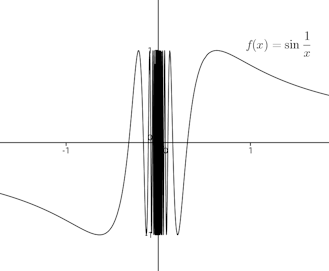
なのだけれど、

　　

のx=0における極限値は

　　

である。

　　

そして、だから、ハサミ打ちの定理より

　　

である。

このあたりが極限の面白さであり、不思議なところであるように思う。

§２　関数の連続

関数の連続の定義

関数f(x)の定義域に属するx=aに対して

　　

であるとき、関数f(x)はx=aにおいて連続であるという。

また、この条件が満たされないとき、f(x)はx=aにおいて不連続であるという。

そして、関数f(x)が定義域に包まれる区間に属すすべての点で連続であるとき、f(x)はその区間で連続という。

また、

　　

のとき、f(x)はx=aにおいて右側連続であるといい、

　　

であるとき、

f(x)はx=aにおいて左側連続であるという。

そして、f(x)がx=aで連続であるとき、

　　

である。

例１

　　

この関数は、x=1で不連続である。

ちなみに、

　　

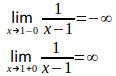
例２

　　

という関数があるとする。

この関数は初項x²、公比1/(1+x²)とする等比数列の無限級数で定義される。

x=0のとき、
　　

x≠0のとき

　　

だから、この無限級数は

　　

に収束する（※）。

したがって、

　　

よって、x=0でこの関数は不連続。

この関数の場合、

　　

つまり、x=0において右側極限=左側極限であるけれど、f(0)=0でないので不連続。





（※）

タグ：微分積分

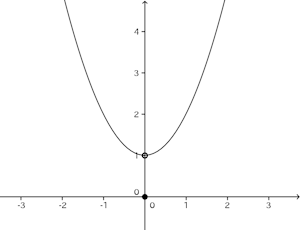
ベクトル 図形への応用

ベクトル　図形への応用

本格的にベクトルの図形への応用をする前に、知識の確認。

　　

1の||はABとCDが平行であることをあらわす記号。

さらに、

点Cが直線AB上にある必要十分な条件はとなるkが存在することである。

問題１　△ABCの外心をOとし、

　　

となるHをとるとき、次のことを証明せよ。

（１）　Hは△ABCの垂心である。

（２）　△ABCの外心、垂心、重心は１直線上にある。

【証明】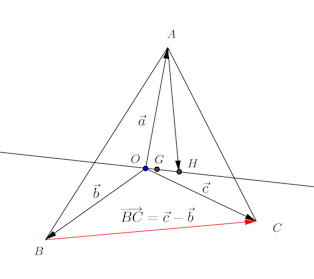

（１）　とする。

Oは△ABCの外心なので、

　　

である。同様に、BH⊥CA、CH⊥AB。
　　
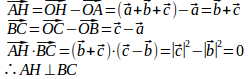
よって、Hは垂心である。

 

（２）　重心をGとすると

　　

だから、

　　

故に、O、G、Hは１直線上にある。

（証明終わり）

オイラー線

三角形において、外心をO、重心をG、垂心をHとすると、O、G、Hは一直線上にあり、

　　

を証明したことになる。

 

問題２　△ABCと同じ平面上に点Oがあり、

　　

であるとき、Oはどんなん点か

【解答】

とすると、条件は

　　

よって、

　　

よって、CO⊥AB。

また、

　　

よって、AO⊥BC。

同様に、BO⊥CA。

したがって、Oは垂心である。

（解答終わり）

問題　３点A、B、Cの位置ベクトルが次の条件を満たしているとき、△ABCはどんな三角形か。

（１）　

（２）　

【解（？）】

重心をGとすると

　　

のときとなり、重心Gと原点Oは一致する。

（１）のはOA=OB=OC、つまり、Oと三角ABCの各頂点の距離は等しいので、Oは外心。外心Oと重心Gが一致するのだから、△ABCは正三角形。

（２）のは、問題２よりOが垂心であることを表しており、また垂心と重心が一致するのだから、△ABCは正三角形である。

（解答？終わり）

 

しかし、こんな解答をしたら、学校の先生から怒られる。学校の先生から怒られるだけならばまだしも、大学受験で点数をもらえないかもしれない。

【解】

（１）　より　　

　　
よって、AB=AC。

同様に、BC=BA。

よって、△ABCは正三角形。

（２）　

で、
　　

よって、AB=AC。

同様に、BC=BA。

よって、△ABCは正三角形。

（解答終わり）

これはあくまで解答の一例で、他にもいくつか解答は考えられる。

たとえば、次のように考えるだろう。

　　

同様に

　　

だからとなり、という条件が出てきて、（２）を（１）に書き換えることもできる。

（１）、（２）ともに、△ABCが正三角形であるための必要十分な条件なのだから、当たり前の話。

（１）はから

　　

として、

　　

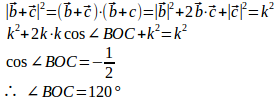
同様に、∠COA=∠AOB=120°。

また、条件よりOA=OB=OC。

２辺挟角相等より△OAB≡△OBC≡△OCA。

よって、AB=BC=CAで△ABCは正三角形。

タグ：ベクトル