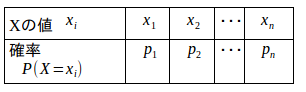第6回 独立試行の確率と2項分布の問題 [ネコ騙し数学]
第6回 独立試行の確率と2項分布の問題
問題1 ❍、☓で答える6つの問題が与えられている。いまこの解答にするのに何も考えずにでたらめに❍、×をつけるとき、そのうちの正解数をXとする。
(1) X≧3になる確率を求めよ。(2) Xの平均値(期待値)と標準偏差を求めよ。
【解】正解数の分布は2項分布。
(1)
(2) 平均値mと標準偏差σは
問題2 日本人の血液型の10人に3人の割合がO型である。5人の日本人を選んだとき、そのうちのO型の人数をXとする。
(1) Xはどのような分布に従うか。(2) Xの期待値と標準偏差を求めよ。
(3) 南方系のある人種から5人を選んだとき、そのうちの4人が O型であった。この人種が日本人よりもOがたが多いと判定したときの危険率を求めよ。【解】
(1) 2項分布B(5,0.3)に従う。(2) 平均値をm、標準偏差をσとすると、
(3) 日本人とO型の割合が等しいと仮定する。
つまり、p=0.3として、P(X≧4)の確率を計算すると
(解答終了)
危険率については検定であらためて説明することにするが、
「南方系のある人種の人たちに占めるO型のヒトの割合が日本人のそれと等しい」という仮説を立てると、5人中4人がO型である確率は0.03で非常にまれなことが起きているということになる。
問題3 さいころを50回投げるとき、1の目が出る回数をXとする。
(1) Xがいくらのとき確率は最大になるか。(2) Xの平均値を求め、(1)で求めた値と比較せよ。
【解】1の目が出る回数は2項分布に従う。
(1) X=kのとき確率が最大とすると、
(2) 平均値(期待値)は
(解答終了)
第5回 独立試行と二項分布 [ネコ騙し数学]
第5回 独立試行と二項分布
§1 独立試行の確率
1回の試行で事象Aの起こる確率をpとすると、この試行をn回繰り返した場合、事象Aがr回起こる確率は
問1 袋の中に赤球1個、白球4個が入っている。この中から1個取り出して、もとに戻すことを3回繰り返す。この場合、赤の出る回数をXとして、Xの確率分布を求めよ。
【解】取り出した球を戻すので、赤球の出る確率p=1/5、白球の出る確率q=4/5。
この問題の場合n=3。Xの取りうる値は0、1、2、3。
X=rの時の確率をP(X=r)と書くことにすると、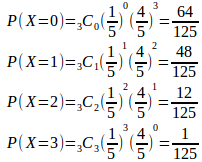
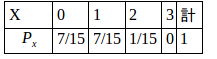
したがって、確率分布は次のようになる。
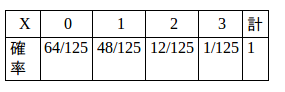
(解答終了)
この問題には出ていないけれど、赤球の出る回数rの期待値mは
§2 2項分布
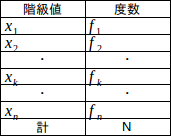
変量Xが0、1、・・・・・・、nの値をとり、それらの値をとる確率が
その平均・期待値m、標準偏差σは
(2)、(3)を使えば、問1の平均値、標準偏差は
【(2)の証明】
xで微分すると、
x=1を代入すると、
【(3)の証明】
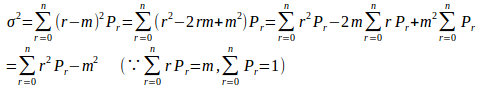
また、
ここで、①の両辺をxで微分すると、
x=1を上式に代入すると、
これを②に代入すると、
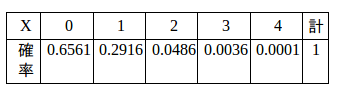
問2 10%の不合格品を含む同じ製品の一山がある。この中から任意に4個を取り出すとき、その中に含まれる不良品の数Xで確率分布の表で示し、Xの平均値、標準偏差を求めよ。
【解】X=rである確率は
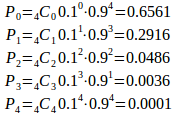
(解答終了)
問題 1回の試行で事象Aの起こる確率がpであるとき、n回の試行の内、事象Aが最も起こりやすい回数を求めよ。
【解】r=kのとき、確率が最大になるとすると、
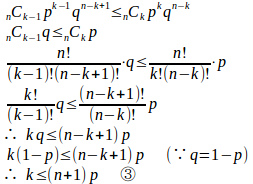
②に対しては、③のkをk+1と置き換えて、不等号の向きを入れ替えると、
(解答終了)
問3 1個のさいころを40回投げるとき、1つの目が何回出る確率が最も高いか。
【解】n=40、p=1/6。
(4)より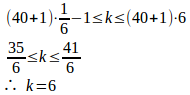
よって、6回のとき確率は最大になる。
(解答終了)第4回 確率分布2 [ネコ騙し数学]
第4回 確率分布2
分布関数と確率密度関数
変数Xが連続な値をとるとき、Xを連続型の確率変数といい、X<xである確率P(X<x)が
変数Xの変域をa≦x≦bとし、確率密度関数をf(x)、平均をm、分散をσ²とすると、
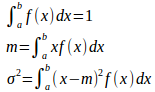
である。
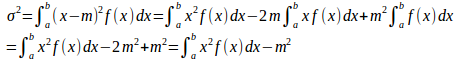
となり、
問題1 確率変数Xの従う確率分布の密度関数f(x)が
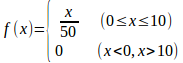
であるとき、次の問いに答えよ。
(1) P(3≦X≦5)の値を求めよ。(2) P(7≦X)の値を求めよ。
(3) Xの平均E(X)を求めよ。(4) Xの標準偏差D(X)を求めよ。
【解】
(解答終了)
問題2 あるバスの停留所の発車時刻は毎時0分、15分、35分の3回である。この発車時刻をまったく知らない人が、停留場へ来て待たされる時間の期待値を求めよ。
【解】この人が停留所に来る時刻をx分とすると、待ち時間tは
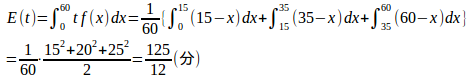
(解答終了)
問題3 連続的な値をとる確率変数xがあって、その確率密度がAを定数として、
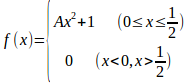
とするとき、となるようなaの値を求めよ。
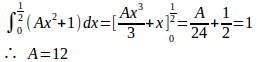
したがって、
a=0.2とすると、
(解答終了)
なのですが、a=0.2であることに気づく人はどれだけいるのだろう。
条件より0<a<0.5で、
とおくと、
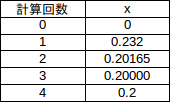 だから、ニュートン法
だから、ニュートン法
計算の初期値としてx₀=0.232を選べば、1、2回計算すれば、a=0.2であることに気づくのではないか。
問題4 半径aの円Oの周上の1点Aから任意の方向に弦を引くとき、それらの弦の長さの平均を求めよ。
また、弦の長さが半径より大となる確率を求めよ。【解】
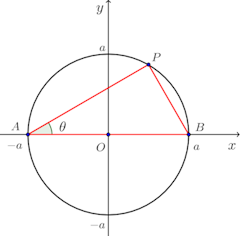 円の中心Oを原点、Aを(−a,0)、Bを(a,0)とし、周上の点をPとする。
円の中心Oを原点、Aを(−a,0)、Bを(a,0)とし、周上の点をPとする。弦APとx軸のなす角をθ(−π/2≦θ≦θ/2)とすると、弦APの長さlは
AP>aになるのは、
第3回 確率変数と確率分布 [ネコ騙し数学]
第3回 確率変数と確率分布
§1 確率変数と確率分布
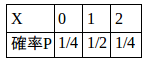
1〜6の目をもつサイコロを振り、出た目をXとすると、Xの目が出る確率は、次のようになる。
![]()
たとえば、X=1と、Xの値が決まれば、その確率
より一般的に書くと、次のようになる。
の値をとる変数Xに対して、
の確率
が与えられているとき、Xを確率変数という。また、確率変数Xとそれに対応する確率
との対応関係を確率分布という。
確率変数のとる値がであるとし、それに対応する確率を
とするとき、
問1 1枚の硬貨を2回投げるとき、表の出る回数を確率変数Xとして、Xの確率分布を求めよ。
【解】(1回目の結果、2回目の結果)と書くことにすると、全事象は、(裏,裏)、(裏,表)、(表,裏)、(表,表)の4通り。
表が0回出るのは、(裏,裏)の1通り。したがって、表が0回出る確率は
したがって、表が1回出る確率は
したがって、表が2回出る確率は
(解答終了)
問2 10本のくじがあって、そのうち、2本が当たりくじとする。3本引いてあたった回数をXとするとき、X本当たる確率を求めよ。
(解答終了)
§2 期待値(平均値)と分散、標準偏差
確率変数Xがの値をとり、それに対応する確率が
であるとき、
をE(x)や、mなどであらわし、確率変数の平均値、期待値という。
をやV(x)、σ²で表し、確率変数の分散という。
問3 白球4個と赤球3個が入っている袋から2個の珠を同時に取り出すとき、その中に含まれる白球の個数の確率分布を求めよ。また、期待値を求めよ。
【解】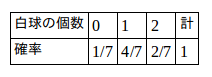 取りざされる白球の個数をk(=0,1,2)に対応する確率を
取りざされる白球の個数をk(=0,1,2)に対応する確率を
したがって、平均値mは
ちなみに、分散Vと標準偏差σは
問題 1と書いたカードが1枚、2と書いたカードが2枚、・・・・・・、nと書いたカードがn枚ある。この中から1枚取り出すとき、カードの示す数Xを確率変数とする。
(1) X=kである確率(2) Xの平均値を求めよ。
【解】(1) カードの数は全部で
したがって、は
(2) Xの平均値mは
第2回 標準偏差と分散 [ネコ騙し数学]
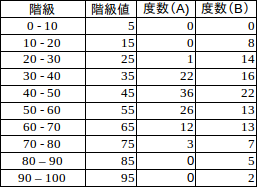 右の(度数)表に表される、2つの異なる試料の集団AとBがあるとする。
右の(度数)表に表される、2つの異なる試料の集団AとBがあるとする。
また、最頻値・モードは45、メディアン・中央値も45である。
それにも関わらず、度数多角形(度数折れ線グラフ)を見ると、資料の値のバラツキ、散らばりの具合が集団Bの方が大きいことがわかる。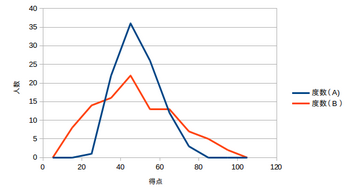
こうした資料の値の散らばりの度合いを示す数を分散度といい、標準偏差はその最も代表的なものである。
N個のの数の平均をmすなわち
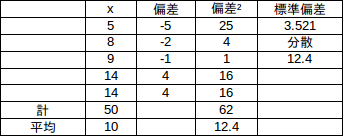 問1 5、8、9、14、14の標準偏差を求めよ。
問1 5、8、9、14、14の標準偏差を求めよ。【解】
平均値mは
−5、−2、−1、4、4
だから(解答終了)
問2 標準偏差は、次の式を用いて計算できることを示せ。
この公式を用い、問1の標準偏差を計算すると、
変量Xの値をの度数分布表が次のようであるとき、Xの平均値をm、すなわち、
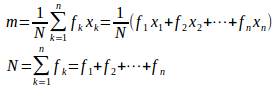
とすると、標準偏差σは
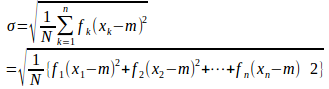
 問3 右の度数分布表から標準偏差を求めよ
問3 右の度数分布表から標準偏差を求めよ【解】
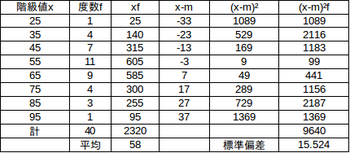
(解答終了)
問4 変数xのとる値を、それぞれの度数を
とし、
xの平均値をm、標準偏差をσとするとき、
【証明】
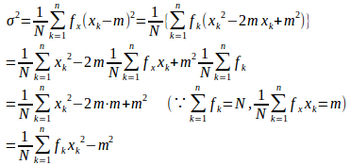
(証明終了)
第1回 資料の整理 [ネコ騙し数学]
第1回 資料の整理
§1 資料の整理
度数分布表
右の図のように、資料をいくつかの階級(区間)に分け、階級ごとの度数を表にしたもの。ここでの階級0〜10は0以上10未満であり、階級の幅は10である。
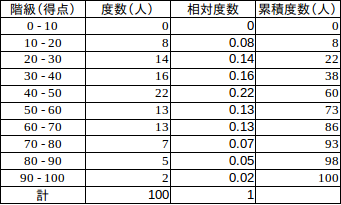
ヒストグラム
横軸に資料の数値、縦軸に度数をとり、階級の幅を1辺、その階級の度数を高さとする長方形を書き、度数の分布を表したグラフ。長方形の面積は、度数に比例する。
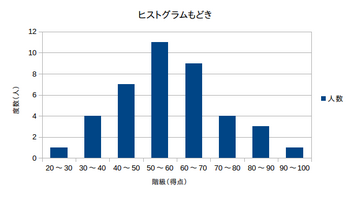
度数分布多角形
ヒストグラムの各長方形の城辺の頂点を順に結び、両端では階級の幅の半分だけ外側に点をとって結んだもの。各長方形の面積の和と度数多角形の面積の和は等しい。
相対度数
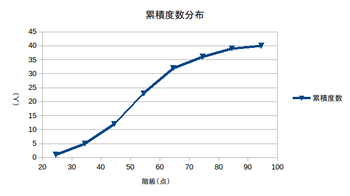
累積度数
各階級までの度数の和を、その階級の累積度数という。§2 代表値
階級値
階級の中央の値上の度数分布表の階級10–20の場合、
(1) 10≦x≦19と考えると
(2)を採用することにする。
平均値
資料の値の総和を資料の総数で割った値N個の値があるとき、平均値mは
である。
モード(最頻値)
度数分布表で最も階級値が大きい階級値
上の例だと、度数が最も大きい階級は40〜50だから、その階級値である45がモードになる。
メディアン(中央値)
資料を大きさの順にならべたとき、中央にくる数値。資料の個数が偶数個のとき、中央の2つの値の平均値とする。
例えば、資料が
また、
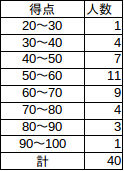
例えば、右 の表の場合、資料の個数は100だから、中央の2つの値は、資料の値の順にならべた、50番と51番目の値。
の表の場合、資料の個数は100だから、中央の2つの値は、資料の値の順にならべた、50番と51番目の値。
累積度数を見ると、これは階級40〜50に属するので、メディアンはその階級値である45になる。
――この値は中学数学レベルの話!!――
私が高校時代に使っていた(受験参考書)にしたがうと、以下のように求める。
総数100、100÷2=50。
累積度数を見ると、これは40〜50の階級に属する。この区間幅は10で、この階級に属する資料の数は22個だから、階級40〜50では40から一様にずつ得点が上昇していると考え、
資料の数が100で偶数だから50番目と51番目の真ん中を50.5番目と考え、
ちなみに、この度数分布表を作成するにあたって用いたデータ
――平均値50、標準偏差20の正規分布もどき――
の50番目と51番目の値は45。中学数学レベルのメディアンの値が元のデータと一致している!!
また、度数分布表から計算した平均値は47.2であるが、元の資料の平均値は46.68で一致しない。
(2)ではなく(1)の階級値を採用すると、平均値は46.7となり、この資料の場合、(1)の階級値を採用したほうが精度は高いようだ。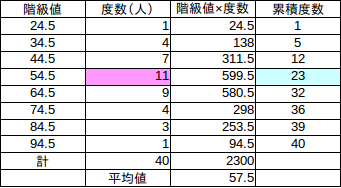
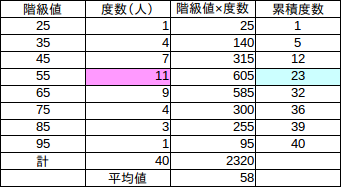
【解】
右の表を元に、次の表を作る。モード(最頻値)は55点。
資料の個数は40なので、中央の値は20番目と21番目の値の平均値。
これは階級値55に属するので、(中学数学の)メディアン(中央値)は55点。高校数学レベルのメディアンは
第15回 数列と確率 [ネコ騙し数学]
第15回 数列と確率
確率と数列の極限の問題を幾つか紹介し、それを解くことにする。
問題1 1つのさいころを振って1が出れば甲の価値、6が出れば乙の勝ちとして、さいころを振ることを止め、1と6以外の他の目が出たら、繰り返して降るものとする。
(1) さいころを振る回数をn回までとしたとき、甲の勝つ確率を求めよ。(2) 回数を制限しないとき、甲の勝つ確率を求めよ。
【解】(1)
したがって、甲が1〜n回で勝つ確率は
(2)
(解答終了)
甲がk回目で勝つ場合は、k−1回連続で2〜5の目が出て、k回目に1が出る場合。
2〜5の目が出る確率は
問題2 ある人が射的をする。一度命中した次に引き続き命中する確率は0.8であり、外れた次に引き続き外れる確率は0.4であるという。第n回目が命中であったときの確率をとするとき、次の問いに答えよ。
(1) を
を用いて表せ。
(2) を求めよ。
(1) 命中した次に命中する確率は0.8
外した後に命中する確率は1−0.4=0.6n−1回目が命中の確率
n−1回目がはずれである確率
したがって、n回目が命中である確率は
したがって、数列は初項
、公比
の等比数列。
(2)
問題3 A、B2人が、A、Bの順で交互にさいころを振り、最初に1の目が出た人を勝ちとする。A、Bの勝つ勝率を求めよ。
【解】p=1/6とすると、Aが勝つパターンは下の表のようになる。
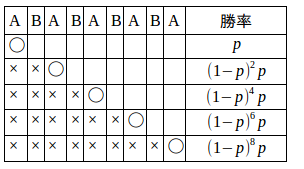
よって、Aが勝つ確率P
したがって、Bの勝率は
つまり、このゲームは先攻の方が有利ということになるのであった。
確率の初歩8 問題編3 [ネコ騙し数学]
確率の初歩8 問題編3
問題1 熊を射ちに行った猟師がある。ねらった銃弾が命中する確率が1/3であるとすると、何発かの弾丸を射って、少なくとも1発命中する確率が0.9以上にするには、何発射てばよいことになるか。
ただし、とする。
n発中少なくとも1発命中する事象は、n発全弾外す事象の余事象である。
ねらった銃弾が命中しない確率は
(解答終了)
問題2 ある高等学校で生徒の血液型を調べたら、O型の者が30%、A型の者が40%であった。この高等学校の生徒3人を無作為に選び出すとき、次の確率を求めよ。
(1) 少なくとも1人がA型である確率(2) 2人がA型で1人がO型である確率
(3) 1人がA型、1人がO型、残りの1人がA型でもB型でもない確率。【解】
(1) 3人ともA型でない確率は
(2) 3人の内、2人がA型、1人がO型である順列の数は
したがって、2人がA型で1人がO型である確率は
(3) 1人がA、1人がO型、1人がA型でもO型でもない順列の数は3!=6。
したがって、この確率は
(2)、(3)の補足説明をする。
(2) 選んだ3人が(A,A,O)の順だとする。生徒数が多ければ1人くらい抜き出しても、生徒に占めるA型の生徒の割合はほとんど変わらない、等しいとみなすことができる。
したがって、この確率は
この他に、(A,O,A)、(O,A,A)の2通りがあり、それぞれの確率が
つまり、①を3倍したものがこの確率になるというわけ。
(3)は、A(割合0.4)、O(割合0.3)確率、AでもOでもない人(割合0.3)の並び、順列が3!=6通りあるので
問題3 20歳の男子が30年以上生存する確率を2/3として、20歳の男子4人のうち、3人以上が30年以上生存する確率を求めよ。
【解】4人のうち3人が30年以上生存する確率P₃は
問題4 n(n≧2)個の正しく作られた硬貨を同時に投げるとき、”すくなくともn−1個裏が出る”という事象をA、”すくなくとも1回表が出るが全部表でない”という事象をBとし、AかつBという事象をA∩Bとあらわすことにする。
(1) を求めよ。
【解】
(1) 事象Aは表が0または1個出る事象だから
n個すべてが表、裏である確率は
nが3以外のとき、AとBは従属。
(解答終了)確率の初歩7 問題編2 [ネコ騙し数学]
確率の初歩7 問題編2
問題1 Aの箱には1個の赤球と2個の青球と3個の白球が入っている。Bの箱には10本のくじが入っていて、そのうち3本が当たりくじである。
Aの箱から1個の珠を取り、それが赤であれば同時3本、青であれば2本、白であれば1本のくじをBの箱から引けるものとする。(1) ちょうど1本当たる確率を求めよ。
(2) 少なくとも1本当たる確率を求めよ。【解】
(1) Aから赤が出てBから1本だけ当たる事象、Aから青が出てBから1本だけ当たる事象、Aから白が出てBから1本だけ当たる事象の確率は、それぞれ、
(2) Aから赤が出て1本も当たらない事象、Aから青が出て1本も当たらない事象、Aから白が出て1本も当たらない事象の確率はそれぞれ
問題2 5個のA、B、C、D、Eを、横に1列に出たらべにならべたとき、次のものを求めよ。
(1) AがBの右にあり、同時にCがDより右にある確率。(2) AとBが隣り合わせにならない確率。
【解】(1) A、B、C、D、Eの5個をならべる順列の総数は5!通り。
AがBの右にあり、同時にCがDより右にある順列の個数は
(2) AとBが隣り合わない事象は、AとBが隣り合う事象の余事象。
AとBが隣り合う順列は、AとBを1個と考え、4個の順列を考えれば良いので、4!通り。したがって、AとBが隣り合う確率は
(※)
次の5つの□のうちに1個を選び、まず、Eをおく。
これには通りの選び方がある。
もっと大胆に考えるならば、AとBを同じ種類、CとDを同じ種類と考え、AとB、CとDを区別しなければよい。区別するから、右・左の順序が生じる。
このように考えると、同じ種類のものを含む順列の公式より
問題3 1つのさいころを4回投げ、1回目に出た目の数をa、2回目に出た目の数をb、3回目に出た目の数をc、4回目に出た目の数をdとする。
(1) a+b+c+dが偶数になる確率を求めよ。
(2) abcdが偶数になる確率を求めよ。【解】
(1) a+b+c+dが偶数になるのは、4回さいころを投げたうち、「偶数の目が4回出る」場合と「偶数の目が2回、奇数の目が2回出る」場合と、「偶数の目が0回出る」場合。偶数の目が出る確率pは
(2) abcdが偶数になる事象の余事象は、「a、b、c、d」がすべて奇数である事象。
4回奇数が出る確率は
「偶数の目が0回出る」確率
確率の初歩6 問題編1 [ネコ騙し数学]
確率の初歩6 問題編1
問題1 1つの袋に赤球3個、白球が7個入っている。この袋から1球取り出し、それが赤球ならばそれで終わりとし、白球ならばそれをもとに戻さないでもう1球取り出すものとする。このとき赤球を取り出す確率を求めよ。
【解】赤球が出るのは、1回目で赤の場合と、「1回目で白球、2回目で赤球」の場合。
1回目に赤球を取り出す確率は
問題2 赤札10枚、白札7枚、青札5枚の計22枚の札がある。この中から4枚取り出すとき、次の事象の確率を求めよ。
(1) 4枚とも赤である。(2) 4枚の札の中にどの色の札も入っている。
【解】(1) 赤札10枚から4枚取り出す組み合わせはしたがって、4枚とも赤である確率は
(2) 4枚の札の中にどの色も入っているのは、「赤札2枚、白札1枚、青札1枚」の場合、「赤札1枚、白札2枚、青札1枚」の場合、「赤札1枚、白札1枚、青札2枚」の場合である。
赤札2枚、白札1枚、青札1枚の場合の確率
問題3 白黒2種の同質の球がある。白球10個と黒球5個を入れたよくかき回し、目をつぶって3個の球を取り出すとき、少なくとも1個は白球である確率を求めよ。
【解】少なくとも1個白球である事象は、取り出した球がすべて黒球である事象の余事象。
3個取り出した球がすべて黒である確率は
問題4 2つの事象A、Bが独立であるとして、Aは起こらないがBは起こる確率をp、AもBも起こらない確率がqとおく。このとき、Aの起こる確率、Bの起こる確率を、pとqであらわせ。
【解】Aの起こる確率をx、Bの起こる確率をyとする。
さらに、Aの余事象、Bの余事象を、それぞれ、であらわすことにする。
①+②
問題5 平均して3問中2問解く能力を持つ学生が、3問の出題で少なくとも2問解ければ合格、正解1問以下では不合格という試験を受けるとき、合格する確率を求めよ。
【解】合格するには、3問、または、2問正解でなければならない。
3問解ける確率は、