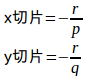ワンポイントゼミ6 極大と極小 [ネコ騙し数学]
ワンポイントゼミ6 極大と極小
極大、極小の定義
関数f(x)が点x=x₀においてとる値f(x₀)がx₀の近傍(x₀を含む十分小さな開区間)で、x≠x₀ならばf(x₀)>f(x)(f(x₀)<f(x))であるとき、f(x)はx=x₀で極大(極小)といい、f(x₀)を極大値(極小値)という。極大値、極小値をあわせて極値という。
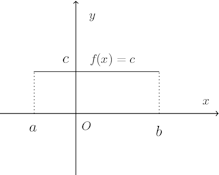
問1 定義域をa≦x≦b(a<b)とする定数関数f(x)=cがある(cは定数)。
f(x)が極大、極小になる点とその値を求めよ。極大、極小になる点、極大値、極小値は存在しない。
(おしまい)
x₀≠xならばf(x₀)>f(x)=c(f(x₀)<f(x)=c)である点x₀がx₀∈[a,b]に存在しない――そのような点x₀が存在するとすれば、f(x₀)>c(f(x₀)<c)になってしまい、f(x₀)=cに矛盾する――。したがって、この場合、極大値、極小値とも存在しない。
問2 実数全域で定義された次の関数f(x)がある。
【答】
f(x)は
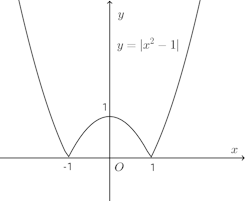
x=−1の十分に近いところにおいて、x≠−1ならばf(x)>f(−1)=0が成立するので、x=−1で極小。
x=1の十分に近いところにおいて、x=1ならばf(x)>f(1)=0が成立するので、x=1で極小。x=0の十分に近いところにおいて、f(x)<f(0)=1だから、f(x)はx=0で極大。
したがって、
極小値0 (x=±1)極大値0 (x=0)
(おしまい)関数が微分可能であるとき、極値をとる点aでは、かならず、f'(a)=0でなければならない。
問2の関数は、x=±1以外では微分可能で、その導関数f'(x)はだからx=0でf'(0)=0となり、この条件を満たしている。
しかし、x=±1で、f(x)は微分可能でないから、この条件を満たしていない。そもそも、導関数f'(x)はx=±1で定義されていない。
また、f(x)=x³は実数全域で微分可能であるけれど、f'(x)=3x²=0となる点x=0で極値をとらない。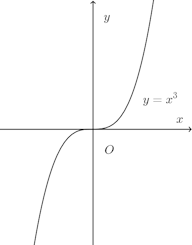
このことから、f'(a)=0という条件は、微分可能な関数f(x)がx=aで極値をもつための十分な条件でないことがわかる。f'(x)=0という条件は、微分可能な関数f(x)が極値を持つために満たさなければならない、必要な条件にすぎない!!
ひとつ質問をするが、
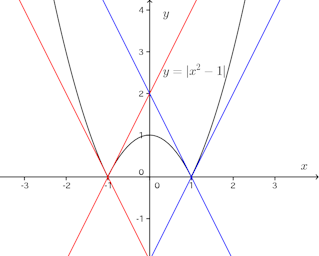
赤と青で示されている直線がこの曲線の接線?
それとも、これとは違う他の直線。
あるいは、接線は存在しない(^^)
3次方程式2 [ネコ騙し数学]
3次方程式2
問題1 3次方程式x³+px+q=0が重複解をもつとき、
【解】
f(x)=x³+px+qとおき、3次方程式f(x)=x³+px+q=0の重複解をαとすると、
(解答終わり)
②の微分のところでは、次の微分公式を使っている。
問題2 3次方程式x³+px²+q=0が重複解をもつとき、pとqにはどのような関係があるか。
【解】f(x)=x³+px²+qとおき、αを重複解とすると、
よって、
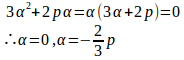
(1) α=0のとき、①よりq=0。
(2) のとき、これを①に代入すると
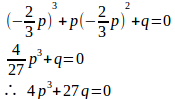
よって、
4p³+27q=0、または、q=0。(解答終わり)
ちなみに、p=q=0のときは、3重解でx=0が解。
問題3 a、b、cが相異なる実数で、
一見すると、3次方程式とは関係なさそうな問題ですが・・・。
【解】
3次方程式の解と係数の関係より、
よって、f(t)はで極小値をとる。
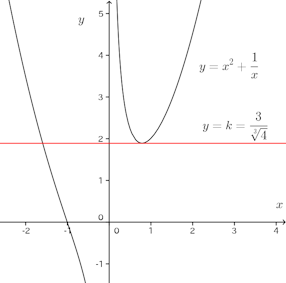
f(x)=kの実数解の個数とy=kとy=f(x)の交点の個数は等しいので、相異なる③つの実数解をもつためには
次のように、y=x³+1とy=kxとの交点の数を調べて、kの範囲を定めてもよい。。
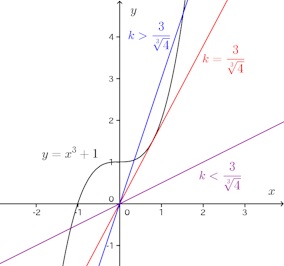
曲線y=x³+1上の点(t,t³+1)における接線の方程式は
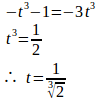
この時の傾きは
したがって、y=kxがy=x³+1とに接するとき
ワンポイントゼミ5 問題4の別解 [ネコ騙し数学]
ワンポイントゼミ5 問題4の別解
記事「3次方程式」の問題4の別解を紹介する。こちらのほうが素直な解答。
問題4 3次関数y=x³+4x²+kx−18のグラフがx軸に接するように定数kの値を定めよ。
【解】f(x)=x³+4x²+kx−18とおくと、f'(x)=3x²+8x+k。
f(x)がx軸と接するから、接点のx座標をαとすると、f(α)=0、f'(α)=0でなければならない。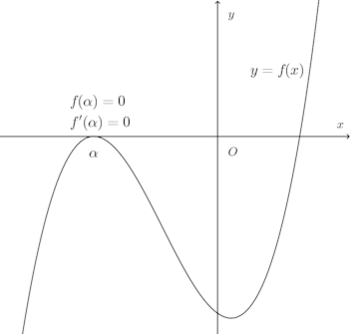
したがって、
(解答終わり)
このように解いてもよい。
【註】
因数定理
整式f(x)がx−aを因数にもつ必要十分な条件はf(a)=0である。
g(−3)=0だから、因数はx−(−3)=x+3。
x−3ではないので、注意!!3次方程式 [ネコ騙し数学]
3次方程式
問題1 x³+x−8=0は、ただ1つの実数解を、1と2の間にもつことを示せ。
【解】f(1)=−6、f(2)=2だから、中間値の定理より、f(x)=0を満たすxが1<x<2に存在する。
f(x)=x³+x−8とすると、
したがって、f(x)=x³+x−8=0を満たす実数解は、1と2の間にただ一つである。
(解答終わり)
問題2 3次方程式x³+x²−x+a=0の実数解の個数がaの値によってどう変わるか調べよ。ただし、重複解は1つと数える。
x³+x²−x+a=0の実数解は
①式を微分すると
x | … | −1 | … | 1/3 | … |
y' | − | 0 | + | 0 | − |
y | 減少 | −1 | 増加 | 5/27 | 減少 |
したがって、
a>5/27、a<−1のとき、実数解は1個
a=5/27、a=−1のとき実数解は2個(重複解が1つ)−1<a<5/27のとき実数解は3個
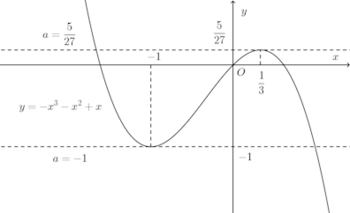
(解答終わり)
問題3 3次方程式2x³+3x²−12x+a=0が重複解をもつようにaの値を定めよ。また、そのときの解を求めよ。
問題2と同じように、y=−2x³−3x²+12xとy=aの共有点の個数を調べてもいいが、次のように解くこともできる。
【解】
f(x)=2x³+3x²−12x+aとすると、
したがって、f(x)=0とf'(x)=0が共通解をもつならば、x=−2またはx=1でなければならない。
(1) x=−2が重複解の場合
(2) x=1が重複解のとき
【別解1】
f(x)=2x³+3x²−12x+a=0の重複解をα、もうひとつの解をβとすると、
したがって、
(1) α=−2のとき
aは
(2) α=1のとき、
(別解1終わり)
微分を使わずに、次のように解くこともできる。
【別解2】αを重複解、βをもうひとつの解とする。
(2) α=1のとき
(別解2終わり)
問題4 3次関数y=x³+4x²+kx−18のグラフがx軸に接するように定数kの値を定めよ。
【解】y=x³+4x²+kx−18がx軸に接するということは、3次方程式x³+4x²+kx−18=0が重複解をもつということ。
3次方程式x³+4x²+kx−18=0の重複解をα、もうひとつの解をβとすると、
③より
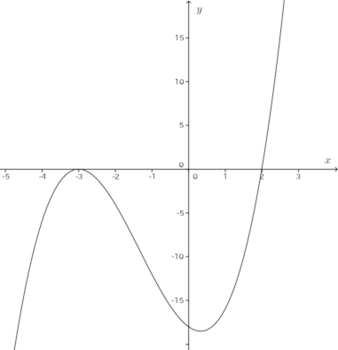
(解答終わり)
ワンポイントゼミ4 微分を用いて、整式を(x−a)²で割った余りを求める [ネコ騙し数学]
ワンポイントゼミ4 微分を用いて、整式を(x−a)²で割った余りを求める
問題 f(x)を2次以上の整式とする。
(1) f(x)を(x−a)²で割ったときの余りが
(2) f(x)がf(x)を(x−a)²で割り切れるための必要十分条件がf(a)=f'(a)=0であることを証明せよ。
(3) x⁷−2x+4を(x−1)²で割った余りを求めよ。【解】
(1) f(x)をf(x)を(x−a)²で割った商をQ(x)、余りをpx+qとすると
(2)
【⇒の証明】(1)より、f(x)を(x−a)²で割ったときの余りは
したがって、
これが任意のxについて成り立つので、
⑥より
【逆の証明】
f(x)を(x−a)²で割ったときの余りは
したがって、
f(x)がf(x)を(x−a)²で割り切れるための必要十分条件がf(a)=f'(a)=0である。
(3)
となる。
もちろん、
と計算してもよい。また、同様の議論から、
したがって、F(x)が整式であるとき、y=F(ax+b)をxで微分すると
話を元に戻すが、
問題より、f(x)が整式であるとき、f(x)=0が重複解(重根)を持つための必要十分な条件は
剰余の定理と因数定理、そして、解と係数の関係 [ネコ騙し数学]
剰余の定理と因数定理、そして、解と係数の関係
§1 剰余の定理
剰余の定理
整式f(x)をx−aで割った余り(剰余)はf(a)である。【証明】
多項式f(x)をx−aで割った商をQ(x)、余りをRとすると、
問 x²−3x+4をx−1、x−2で割った余りを求めよ。
【解】f(x)=x²−3x+4とおく。
剰余の定理より、f(x)をx−1で割った余りR₁は
問題1 xについてある整式をx−2で割ると5余り、x−3で割ると8余るという。この整式を(x−2)(x−3)で割った余りを求めよ。
【解】xについての整式をf(x)、(x−2)(x−3)で割った商をg(x)、余りをax+bとする(※)。
題意より
よって、余りは3x−1である。
(解答終わり)(※) 整式f(x)を2次式(x−2)(x−3)で割った余りは、高々1次式なので、その余りをax+bと置くことができる。
§2 因数定理
因数定理
整式f(x)がx−aを因数にもつ必要十分な条件はf(a)=0である。【証明】
f(x)をx−aで割った商をQ(x)、余りをRとする。(必要条件の証明)
したがって、
よって、f(x)はx−aで割り切れ、f(x)はx−aを因数にもつ。
(証明終わり)問 次の方程式を解け。
f(x)=x³−3x²−4x+12とおくと、
x−2でf(x)を割ると、商はx²−x−6。
だから、よって、この方程式の解はx=±2、3である。
(解答終わり)§3 2次方程式と3次方程式の解と係数の関係。
(1) 2次方程式の解と係数の関係2次方程式の一般形は
したがって、
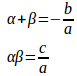
これを2次方程式の解と係数の関係という。
問題 2次方程式x²−10x+c=0の2つの実根αとβの間にβ=α³の関係が成立するとき、cの値を求めよ。
【解】解と係数の関係より
f(α)=α³+α−10とするとf(2)=0。
よって、
(2) 3次方程式の解と係数の関係
3次方程式の一般形は
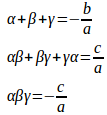
という3次方程式の解と係数の関係が得られる。
問題 方程式x³+ax²+bx−12=0が根3および3と異なる実根をもつとき、重根およびa、bの値を求めよ。
【解】3と異なる実根をαとすると、解と係数の関係より
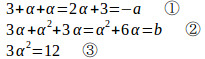
③より
α=2のとき、a=−7、b=16
α=−2のとき、a=1、b=−8(解答終わり)
(a+b)²−(a−b)²をどうやって計算する? [ネコ騙し数学]
一つ質問するけれど、
真面目に展開して、
それとも、
この場合は、①の方が楽だけれど、今日のワンポイントゼミ3にでてきた
あなたは、これを真面目に展開して計算しますか。
オレは、頭の中で、②を使って、
①の結果、
⑧をバカ正直に展開して計算するヒトは、⑨未満と呼ばれてもしょうがない!!
そう、思わないかい?
⑨のチルノですら、間違っているけれど、自身の知識を活用している!!
ワンポイントゼミ3 球の体積 [ネコ騙し数学]
ワンポイントゼミ3 球の体積
半径rの円の体積Vは
このことを定積分を使って求めることにする。
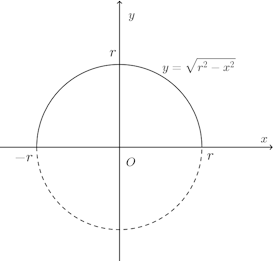
原点Oを中心とする半径rの半円は
は偶関数だから、偶関数の定積分の性質から
途中計算でこれを使っている。
【方法2】
原点を中心とする球の方程式は
この断面の面積S(t)は
方法2の定積分は、方法1の計算のxがtに変わっているだけなので、計算しないけれど、このように計算することもできる。
(※) x=±rにおける球の断面(?)を半径0の円とみなしている。
厳密には
問題 半径rの円
【解】
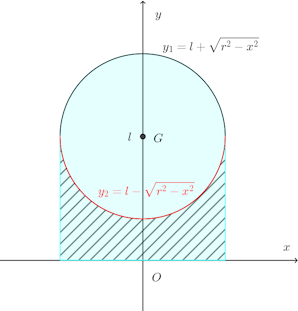
求める体積は、薄い水色で示されている、y₁とx軸とで囲まれている領域を回転してできる立体の体積から、斜線部で示されているy₁とx軸とで囲まれている領域を回転してできる立体の体積を引いたもの。
したがって、
注目して欲しいのは、この結果。
⑨より、問題で求めた円環体の体積Vは
円環体の体積V=(円Cの重心が回転により描く軌跡の長さ)×(円Cの面積)
になっていることがわかる。
これは偶然のことか(^^)
体積の問題2 [ネコ騙し数学]
体積の問題2
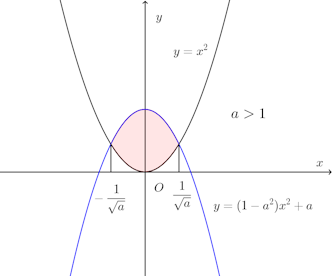
問題1 異なる2つの放物線y=x²、y=(1−a²)x²+aが交わるとき、これらで囲まれる図形をy軸のまわりに回転してできる回転体の体積は、aの値にかかわらず一定であることを証明せよ。ただし、a>0とする。
【解】異なる2つの放物線の交点のx座標は
(1) 0<a<1のとき、体積Vは
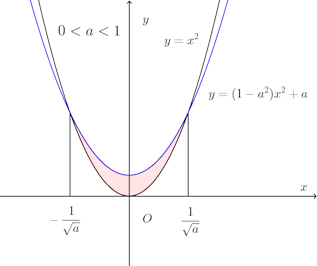
(2) a>1のとき
よって、体積Vはaの値にかかわらず一定で、その値はπ/2である。
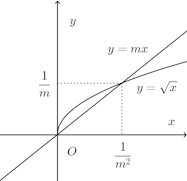
(解答終わり)問題2 曲線y=√xと直線y=mxとで囲まれる図形をx軸のまわりに回転してできる立体とy軸のまわりに回転できる立体
とが同じ体積になるようにmの値を定めよ。
だから
問題2 図のように、AC=1、BC=3とし、DEはA、Bを中心とし点Cで外接する2円の共通接線である。∠ABE=60°であることを示し、斜線をつけた部分CDEをABのまわりに回転して得られる立体の体積を求めよ。
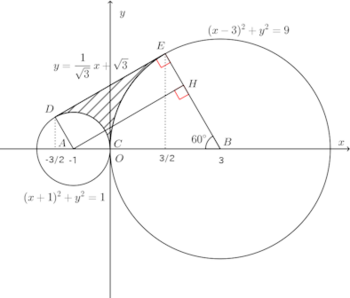
【解】
Cを原点Oにとり、Aを(−1,0)、Bを(3,0)にとる。
Aから直径BEに垂線をおろし、垂線の足をHとする。
四角形ADEHは長方形。
よって、
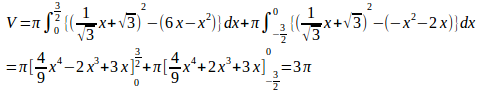
(解答終わり)
ワンポイントゼミ2 x切片とy切片 [ネコ騙し数学]
ワンポイントゼミ2 x切片とy切片
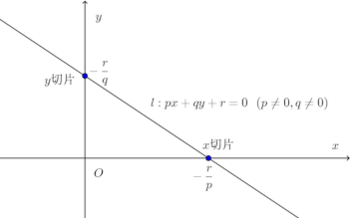
図に示すように、xy平面上に直線l:px+qy+r=0(p≠0、q≠0)があるとする。
このとき、直線lとx軸の交点のx座標が(直線lの)x切片、y軸との交点のy座標をy切片という。つぎに、このときの、x切片とy切片を求めることにする。
直線l上の点はすべてpx+qy+r=0を満たす。
したがって、この交点のx座標をaとおくと、この交点の座標は(a,0)になるので、①式にx=a、y=0を代入して得られる方程式を解くと
x切片a、y切片b(a≠0、b≠0)である直線の方程式を求めることにする。
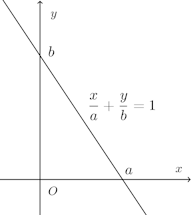
x切片がaだから、x=a、y=0を①に代入すると、
r=0のとき、px+qy=0で、この直線は原点Oを通ることになり、a≠0、b≠0と矛盾する。したがって、r≠0。
r≠0だから、②式の両辺をrで割り、
問 次の直線の方程式を求めよ。
(1) x切片2、y切片3の直線(2) 2点、(0,2)、(0,3)をとおる直線
実は、(1)と(2)は同じことを言っている。そして、この答えは③より
無理に覚える必要はないけれど、③式はおぼえておくと、何かと便利である。
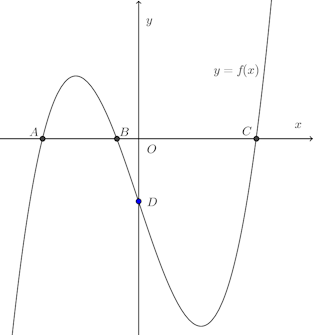
より一般に、y=f(x)とx軸との交点のx座標をx切片、y=f(x)とy軸との交点をy切片という。
図に示すように、曲線y=f(x)の場合、点A、B、Cのx座標が曲線y=f(x)のx切片であり、点Dのy座標が曲線y=f(x)のy切片である。この図、その定義から明らかであるけれど、曲線y=f(x)のx切片は方程式