空間曲線 [ネコ騙し数学]
空間曲線
空間の点Pの描く空間曲線は
で与えられるが、これは原点Oを始点とする点Pの位置ベクトルが
と与えられることと同等である。
そして、接線ベクトルは
で与えられる。
さらに、この曲線Cが滑らかなとき、位置ベクトルr(a)からr(t)までの弧の長さs(t)は
となり、
となり
よって、
となる。
dsを線元素という。
sはtの関数であるが、逆にtもsの関数と考えられるので、曲線は、曲線の長さを用いて
r=r(s)
とあらわすことが可能。
は曲線に接しsの増加する方向に向かうベクトルである。
何故ならば、
で、ベクトルtの向きは接線ベクトルdr/dtと同じだから。
sとs+Δsに対応する曲線上の点をP、Qとし、とすれば
だから、tは単位接線ベクトルである。
Qにおける接線ベクトルとPにおける接線ベクトルのなす角度をΔθとすれば、
は、曲線の長さに対する接線の向きの変化率をあらわし、
を点Pにおける曲率という。この定義から明らかなように曲率は正または0であり、曲線上の各点でκ=0である時は、この曲線は直線である。
単位法線ベクトルt同士の内積t・t=1を微分すると、
となり、はtに垂直である。また、
と同じ向きの単位ベクトルをnとすれば、
このnをPにおける(単位)主法線ベクトルといい、
となる。
また、曲率は
曲率の逆数
を曲率半径といい、曲線上のPから引かれたベクトルρnの終点を曲率半径の中心という。
また、曲線上の点Pにおける接線ベクトルと主法線ベクトルの外積
b=t×n
を、点Pにおける曲線の(単位)従法線ベクトルという。
したがって、
t、n、bは互いに直交する単位ベクトルで、右手系をなす。
また、
が成立し、τを捩率(れいりつ)という。
b・b=1なのでこれをsで微分すると
となり、bとは直交する。
さらに、t・b=0をsで微分すれば、
となる。
なので、第2項はκn・b=0である。よって、
となり、tとは垂直。
故に、 はbとtに垂直であり、nと同じ方向である。
t、n、bの3つの単位ベクトルは右手系を構成するので、
n=b×t=−t×b
となる。
これをsで微分すると、
となる。
の3つの公式を合せてフルネ・セレの公式と呼ぶ。
空間曲線のベクトル方程式と接線ベクトル [ネコ騙し数学]
空間曲線のベクトル方程式と接線ベクトル
空間曲線は、スカラー変数tを用いて
であらわすことができる。
曲線上の任意の点P(x,y,z)とし、とおけば、rはtの関数だから、
と書き、これを曲線ベクトル方程式という。
とすると、Δt≠0のとき
はに平行である。
したがって、
は、曲線の接線ベクトルと平行であり、これを曲線の接線ベクトルという。
また、
を単位接線ベクトルという。
単位接線ベクトルtは大きさが1で変わらないので、
したがって、tとは直交する。そこで、
を曲線r(t)の法線ベクトルといい、
を主法線ベクトルという。
また、曲線上の点における単位接線ベクトルtと単位主法線ベクトルnとの外積
ベクトルを(単位)従法線ベクトルという。
曲線r=r(t)は、r'(t)が連続で常にr'(t)≠0であるとき、滑らかな曲線という。滑らかな曲線r=r(t)のa≦t≦bの部分の長さを弧長といい、弧長sは
![]()
で与えられる。
問1 の単位接線ベクトルと、単位法線ベクトルを求めよ。また、t=π/4のときの接線の方程式を求めよ。
【解】
よって、単位接線ベクトルtは
また、
よって、単位法線ベクトルnは
である。
t=π/4の接線ベクトルは
よって、接線の方程式は
tを消去し
(解答終)
t=π/4のときの、接線の法線ベクトルnは(-1/√2,1/√2)だから、接線の方程式を
と求めることもできる。
問2 曲線の0≦t≦2πの曲線の長さを求めよ。
【解】
(解答終)
ベクトル関数とその微分 [ネコ騙し数学]
ベクトル関数とその微分
実数Rの部分集合Dに属する点tに対して、実関数x(t)、y(t)、z(t)が与えられているとき、ベクトル(x(t),y(t),z(t))を考えることができ、このベクトルF(t)=(x(t),y(t),g(t))をDからR³への1変数ベクトル値関数、または、ベクトル関数という。
Lを定ベクトル、t₀を一定の値とするとき、
ならば、tがt₀に限りなく近づくとき、F(t)はLに限りなく近づくといい、また、LはF(t)の極限といい、
であらわす。
イプシロン・デルタ論法で書くならば、
任意のε>0に対して、あるδ>0があって
が成り立つとき、
とあらわす。
また、
が成り立つとき、F(t)はt=t₀で連続であるという。また、区間Iのすべての点でtで連続であるとき、F(t)はIで連続であるという。
イプシロン・デルタ論法による、ベクトル関数F(t)のt=t₀における連続の定義は次の通り。
任意のε>0に対して、あるδ>0があって
が成り立つとき、F(t)はt=t₀において連続であるという。
ベクトル関数F(t)に関して、次の極限
が存在するとき、F(t)はt=t₀で微分可能という。また、この極限値Aをt=t₀における微分係数といい、
であらわす。
定理
とすると、次が成立する。
(ⅰ)
(ⅱ) F(t)は連続⇔x(t)、y(t)、z(t)は連続
(ⅲ)
この定理はほとんど明らかだと思うので、(ⅰ)だけを証明することにする。
【略証】
(ⅰ) ならば、
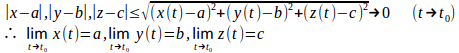
逆に、
ならば

(証明終)
ベクトル関数の微分については、実関数の微分と同様に次の公式が成り立つ。すなわち、A=A(t)、B=B(t)をtのベクトル関数m=m(t)をtのスカラー関数とすると、
である。
例1 Cが一定のベクトルのとき、
例2 mが定数のとき、
問題1 Aをtのベクトル関数とするとき、次のことを示せ。
(1)
ここで、A²=A・Aとする。
(2) |A|が一定であるとき、A とは直交する。
【解】
(1)
(2) |A|は一定だから、A²=A・A=|A|²も一定。
したがって、
また、(1)の結果より
よって、A とは直交する。
(解答終)
問題2
【解】
![]()
(解答終)
問題3 A(t)の微分係数をAの方向とこれに垂直な方向とに分解せよ。
【解】
Aと同じ方向の単位ベクトルをa、Aの大きさをAとすると、
aは単位ベクトルだから問題1より、aとは直交するので、
である。
(解答終)
A(t+Δt)とA(t)のなす角をΔθ、単位ベクトルaの増分をΔaとすると、
と同じ方向の単位ベクトルをbとすると、
だから、問題3の(1)は
である。
ベクトルの内積、外積 [ネコ騙し数学]
ベクトルの内積、外積
§1 ベクトルの内積(ベクトルのスカラー積)
をaとbの内積といい、記号a・bや(a,b)などであらわす。すなわち、
である。
内積はスカラーで、bのaへの正射影を、aのbへの正射影を
とすれば、
である。
a、bがともに零ベクトルでないとき、(1)式より、内積はθが鋭角ならば正、直角ならば0、鈍角ならば負である。また、a、bのいずれかが零ベクトル0であるとき、内積は0である。
ベクトルの内積に関しては、交換、結合法則が成り立つ。すなわち、
mをスカラーとすると、さらに、
が成り立つ。
先に述べたように、ベクトルaとベクトルbのなす角θが直角のときa・b=0である。
逆にa・b=0のとき、
(ⅰ) aとbのなす角θが直角
(ⅱ) a=0またはb=0
である。
特に、基本ベクトルi、j、kに対しては
である。
したがって、
ベクトルa、ベクトルbの成分を(a₁,a₂,a₃)、(b₁,b₂,b₃)とすれば、内積a・bは
で、aとbのなす角の余弦は、(1)、(2)式より
問1 a=2i–3j+5k、b =–2i–2j+2kが垂直であることを示せ。
【解】
よって、垂直である。
(解答終)
問2 a=2i–3j+kとb=3i–j–2kのなす角を求めよ。
【解】
(解答終)
問3 a=2i–3j+kのb=3j–4k上への正射影を求めよ。
【解】
aのb上への正射影は
である。
よって、
(解答終)
§2 ベクトルの外積(ベクトルのベクトル積)
 平行でない2つのベクトルa、bを隣り合う2辺とする平行四辺形をもとに
平行でない2つのベクトルa、bを隣り合う2辺とする平行四辺形をもとに
(1) 大きさは、この平行四辺形の面積に等しい
(2) 向きは、この平行四辺形のある平面に垂直で、aからbへ右ネジをまわすときネジの進む方向と同じ
であるベクトルを作る。
このようにaとbから作ったベクトルをaとbの外積、または、ベクトル積といい、記号a×bであらわす。
aとbのなす角をθとすると、外積の大きさは
である。
aとbが平行のとき、およびaまたはbが零ベクトルであるとき、
と定義する。
a×b≠0のとき、a×bはb×aと大きさが等しく向きが反対だから
すなわち、ベクトルの外積は交換法則が成立しない。
しかし、分配法則は成り立ち、
さらに、
i、j、kを基本ベクトルとすると、
ベクトルaとベクトルbの成分をそれぞれ(a₁,a₂,a₃)、(b₁,b₂,b₃)とすると、外積は、分配法則が成り立つので、
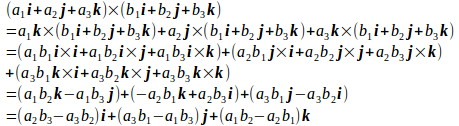
これを行列式で書くと
である。
ディラックのデルタ関数 [ネコ騙し数学]
ディラックのデルタ関数
ディラックのデルタ関数δ(x)とは、次の性質をもつ超関数のことである。
このディラックのデルタ関数の性質を調べるためには、通常の微分積分の範囲を超える数学の知識が必要になるので、物理の本を参考にして、デルタ関数の性質をいくつか紹介することにする。
まず、
x≠0ではδ(x)=0だから、x≠0のf(x)の値は積分の値に無関係で寄与しない。
したがって、
また、
である。
これは、x–a=tとおくと、x=t+a
この積分の値に関係するのは、 (1)からt=0のときのf(t+a)の値。
したがって、
次に
である。
f(x)を任意の関数とする。
よって、
である。
さらに、
f(x)を任意の関数にすると、
t=−xとおくと、x=−tだから、x=−∞はt=∞、x=∞はt=−∞に対応する。
また、dx=−dtだから
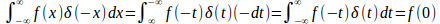
したがって、
である。
さらにさらに、
f(x)を任意の関数とする。
を考える。ax=tとおくと、dx=dt/aだから
よって、
である。
最後に、デルタ関数の微分
f(x)を任意の関数とし、次の積分を考える。
−x=tとおくと、
これに部分積分を施すと、
また、
![]()
したがって、任意の関数f(x)について
以上のことをまとめると、ディラックのデルタ関数には次のような性質がある。
(ⅰ)はデルタ関数δ(x)が偶関数であることを表し、デルタ関数の導関数δ'(x)が奇関数であることを表している。
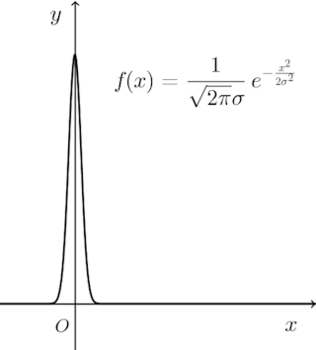
の極限で与えられることが知られている。
したがって、デルタ関数は正規分布の密度関数の一種と考えることができる。
曲率円(接触円)を求める [ネコ騙し数学]
曲率円(接触円)を求める
曲線y=f(x)上の点P(x₀,f(y₀))における曲線y=f(x)の曲率円(接触円)を求める前に、復習。
曲率円
曲線y=f(x)上の点P(x₀,y₀)において
で定まる円
を曲率円(接触円)という。
問題 次の曲率円を求めよ。
(1) 放物線y=x²上の点x=0とx=1における曲率円。
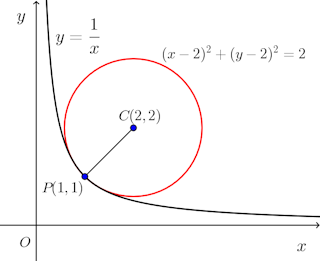
(2) 双曲線y=1/x上の点x=1における曲率円。
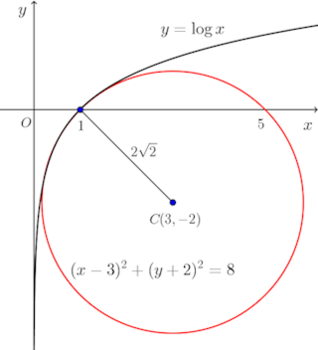
(3) 曲線y=logx上の点x=1における曲率円。
【解】
 (1) y=f(x)=x²だから、f’(x)=2x、f''(x)=2。
(1) y=f(x)=x²だから、f’(x)=2x、f''(x)=2。
x=0ではf(0)=0、f'(0)=0、f''(0)=2。
したがって、曲率円は
である。
 x=1では、f(1)=1、f'(1)=2、f''(1)=2。
x=1では、f(1)=1、f'(1)=2、f''(1)=2。
よって、x=1における曲率円は
である。
(2) y=f(x)=1/xだから、
x=1では、f’(1)=−1、f''(1)=2
よって、x=1における曲率円は
である。
(3) y=f(x)=logxとおくと、
である。
x=1では、f(1)=0、f'(1)=1、f''(1)=−1。
よって、x=1における曲率円は
(解答終)
曲率と曲率半径 [ネコ騙し数学]
曲率と曲率半径
曲率とは曲線や曲面の曲がり具合をあらわすもので、曲率半径は曲率の逆数である。
問題 半径rの任意の円の微分方程式を作れ。
【解答】
円の中心を(a,b)とすると、半径rの円の方程式は
①の両辺をxで微分すると、
②の両辺をxで微分すると
②と③より
③と④を①に代入して、a、bを消去すると
よって、
(解答終)
 もし、x=x₀の近傍で曲線y=f(x)を局所的に円に近似できるとすれば、⑤式からこの近似した円(曲率円)の半径(曲率半径)を
もし、x=x₀の近傍で曲線y=f(x)を局所的に円に近似できるとすれば、⑤式からこの近似した円(曲率円)の半径(曲率半径)を
求めることができる。
また、②と③式より、円の中心(a,b)は
と求められる。
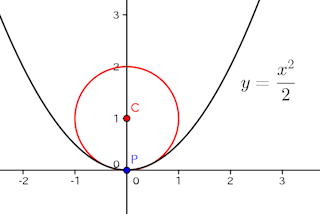
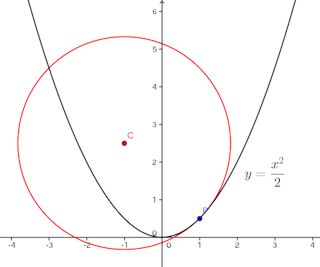
試しに、⑥式を用いて、放物線y=x²/2の点xにおける曲率円の半径を求めてみると、
よって、x=0のとき曲率半径r=1、x=0のとき曲率半径r=2√2になる。
図を見ると、x=0、ならびに、x=1の近傍の放物線を曲率円が表していることがわかるであろう。
以上のことをまとめると、次のようになる。
曲率円
曲線y=f(x)上の点P(x₀,y₀)において
で定まる円
を曲率円(接触円)という。
さて、一般論。
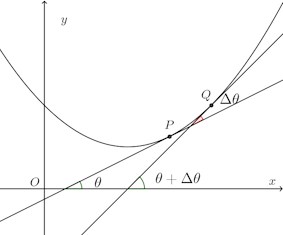 曲線上の点P(x,y)における接線とx軸のなす角をθ、曲線上でPに近い点Qにおける接線'がx軸となす角をθ+Δθとし、弧PQの長さをΔsとするとき、
曲線上の点P(x,y)における接線とx軸のなす角をθ、曲線上でPに近い点Qにおける接線'がx軸となす角をθ+Δθとし、弧PQの長さをΔsとするとき、
を2点P、Q間の平均曲率といい、
(の絶対値)を曲率、この逆数を曲率半径という。
半径rの円があり、円周上の2点P、Qとこの円の中心のなす角、すなわち中心角をΔθとすると、弧PQの長さΔs=rΔθだから、
となるので、何故、曲率の逆数が曲率半径になるのかが分かるのではないか。
この両辺をxで微分すると、左辺は
![]()
だから、
また、
だから、
したがって、曲率と曲率半径κは
である。
点Pにおいて曲線に接し、接線に関して曲線と同じ側にあって、半径が|κ|に等しい円を曲率円といい、その中心)を曲率円の中心という。
問 y=x³の曲率を求めよ。
【解】
したがって、
(解答終了)
直交曲線群 [ネコ騙し数学]
直交曲線群
パラメータc、1個の平面曲線群
のすべての曲線に一定の角度αで交わる曲線を等角直線といい、とくにα=±π/2(α=±90°)のとき直交曲線という。
微分方程式
で与えられる曲線群に対する直交曲線群の微分方程式は
である。
 曲線y=φ(x)に点P(x,y)でy=ψ(x)で直交するとすると、すなわち、点Pにおけるy=φ(x)とy=ψ(x)の接線が直交するとすると、この曲線の接線の傾きφ'(x)とψ'(x)の積は−1。
曲線y=φ(x)に点P(x,y)でy=ψ(x)で直交するとすると、すなわち、点Pにおけるy=φ(x)とy=ψ(x)の接線が直交するとすると、この曲線の接線の傾きφ'(x)とψ'(x)の積は−1。
したがって、
(1)に代入すると、
ここで、改めて
とおくと、(1’)は(2)になるというわけ。
例題 放物線y=ax²(a≠0の任意実数)に直交する曲線群の方程式を求めよ。
をxで微分すると、
①×2−②×x
x≠0とすると、
曲線y=ax²に点P(x,y)における曲線の傾きをとすると、
xy≠0のとき、
したがって、
xy=0のとき、y=ax²はx軸に接するからy=0は直交する曲線になる(特異解)。
したがって、とy=0が直交曲線群である。
(解答終)
y=ax²を、
x≠0のとき
と変形し、さらに、この両辺をxで微分し
として、aを消去することもできる。
問題 次の曲線群と直交する曲線群を求めよ。
【解】
の両辺をxで微分すると、
P(x,y)においてxy=kに直交する曲線の勾配をdy/dxとすると、
(2)
の両辺をxで微分すると、
y–1≠0のとき
P(x,y)においてxy=kに直交する曲線の勾配をdy/dxとすると、
を変数分離法で解くと、
y=1は円群x²+y²+2x–2y+C=0に直交し、これは①のa=0の場合(特殊解)(※)。
x=−1も円群x²+y²+2x–2y+C=0に直交する(特異解)。
(解答終)
第22回 包絡線 [ネコ騙し数学]
第22回 包絡線
αをパラメータとして含む曲線群
の各曲線と1点だけで接する曲線を、この曲線族の包絡線という。
f(x,y,α)をC¹級とする。曲線群と包絡線の接点を(x,y)とすると、xとyはαの関数である。
これを
とする。
(1)と(2)は接するのだから、
また、φ(α)、ψ(α)はf(x,y,α)=0上の点だから
これをαで微分すると、
よって、包絡線は、2曲線
の交点(φ(α),ψ(α))=0の軌跡であり、この2式からαを消去した方程式の曲線Cに含まれる。そして、曲線Cは曲線群の特異点を含むことがある。5E23D0-houraku-graph-001-fdfd5.png) 例
例
この場合、はx–α=0。よって、x=αのときy⁴–y²=0となりy=0、±1となるが、点(α,0)は特異点(結節点)なので、直線y=0は特異点(α,0)の軌跡。したがって、包絡線はy=±1である。(右図参照)
問題1 次の曲線群の包絡線を求めよ。
【解】
(1)
①の両辺をαで偏微分すると
①の両辺を②乗すると、
よって、包絡線は放物線y²=4x
(2)
①の両辺をαで偏微分すると、
①と②を2乗して足すと
よって、包絡線は原点を中心とする半径pの円である。
をαで偏微分すると、
したがって、
x=−1は包絡線であり、x=0は特異点の軌跡。
(解答終了)
とすると、
したがって、(0,α)は特異点である。
また、
よって、(x,y)=(0,α)において
よって、(0,α)は結節点で接線は2本引ける。
問題2 次の包絡線を求めよ。
(1) 円x²+y²=r²のy軸に平行な弦を直径とする円の曲線群
(2) 座標軸で切り取られる部分の長さが一定である曲線群
【解】
( 1) 弦の両端をA、B、その中点をCとし、C(α,0)とする。
1) 弦の両端をA、B、その中点をCとし、C(α,0)とする。
三角ACOは直角三角形だから、ABを弦とする円の半径ACは
よって、円の方程式は
αで偏微分すると、
これを①に代入すると、
(2) 直線の方程式を
とすると、条件より
①をαで偏微分すると、
②をαで微分すると
③に代入すると、
とおくと、
これを①に代入すると、
②に代入すると、
④を②乗したものと⑤の辺々を掛けると、
よって、アステロイドになる。
(解答終了)
第21回 平面曲線 [ネコ騙し数学]
第21回 平面曲線
§1 通常点と特異点
関数f(x,y)をC¹級の関数とし、(x₀,y₀)を曲線f(x,y)=0上の点とする。と
が同時に0にならないとき(x₀,y₀)を通常点(正則点)といい、
となるとき特異点という。
(x₀,y₀)が通常点のとき、ならばx₀の近傍内にある曲線の一部はy=φ(x)、
ならばx=φ(x)で表される。通常点(x₀,y₀)では接線がただ1つ存在し、その方程式は
である。
例1 f(x,y)=x²+y²–a²= 0(a>0)とすると。
したがって、になるのは(x₀,y₀)=(0,0)であるが、(0,0)は曲線上の点ではないので、曲線f(x,y)=x²+y²–1= 0は特異点を持たず、通常点のみである。
また、曲線(原点を中心とする半径aの円)上の点(x₀,y₀)における接線の方程式は
例2 f(x,y)=y³–x⁴=0とすると、。したがって、(0,0)は特異点。
この曲線は と同一の曲線なので、
となり、φ'(0)=0で、この曲線はx=0でx軸と接している。
例3 f(x,y)=y²–2x²y+x⁴–x⁵= 0とすると、
したがって、(0,0)は特異点である。
y²–2x²y+x⁴–x⁵= 0をyについて解くと、になるので、
したがって、x=0での微分係数は0となり、この曲線はx軸に接している。
この曲線の特異点(0,0)のような特異点を嘴点と呼ぶ
。
§2 特異点の分類
f(x,y)をC²級の関数とし、(x₀,y₀)を曲線f(x,y)=0の特異点とする。が同時に0にならないとき、(x₀,y₀)を2重点という。
とおくと、2重点は次のように分類できる。
(1) D>0ならば結節点で、(x₀,y₀)で相異なる2本の接線が引ける
(2) D=0ならば通常は尖点で、(x₀,y₀)における接線は1本である。
(3) D<0ならば孤立点で、その近傍内にある曲線の部分は(x₀,y₀)だけである。
例2、例3の特異点は、D=0になるので、尖点である。
問題 曲線y²=x²(x+a)の特異点を調べよ。
【解】
f(x,y)=y²–x²(x+a)とおくと、
を解くと、
になる。
a≠0のとき
したがって、特異点は(0,0)のみである。
特異点の判別をするために、f(x,y)の2次偏導関数を求めると、
したがって、
だから、
a>0のときは結節点、
a=0のときは尖点、
a<0のときは孤立点
(解答終了)
参考までに、a=3、a=−3のときの、曲線y²=x²(x+a)の概形を以下に示す。





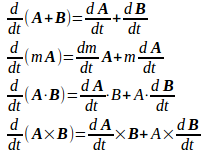

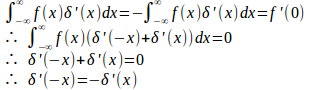
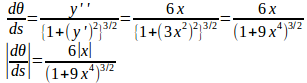


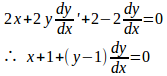





5E23Dx5E2(x2B1)-houraku-graph-001.png)





5E23Dx5E3-graph-001-77516.png)
-graph-03-9cddb.png)

-graph-dea1d.png)



