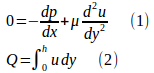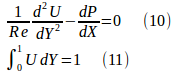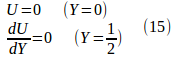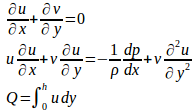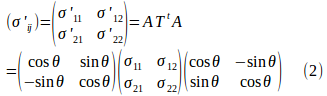連立方程式の解法3 反復法1 [ネコ騙し数学]
連立方程式の解法3 反復法1
ヤコビ法
次の3元連立方程式があるとする。
①をx、②をy、③をzについて解くと次のようになる。
ここで、として上の式の右辺に代入すると、
となる。
このを用いて
さらに、この値を用いて
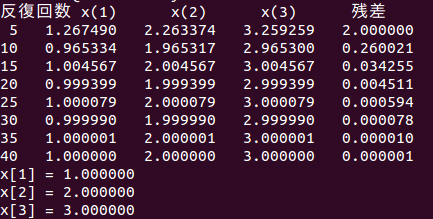
このように繰り返し計算すると、
と、やがて、3元連立方程式の解である(x,y,z)=(1,2,3)に収束してゆく。
このように反復計算をして連立方程式の解を求める方法をヤコビ法という。
より一般の
つまり、
の場合、次のように計算すればよい。
STEP1 1行からn行まで
を計算する。
STEP2 i=1〜nまでのすべてのを
の値に更新する
STEP3 所定の精度に達していなければSTEP1に戻る。達していたら、計算を打ち切る。
いま述べたヤコビ法は、直接、連立方程式の解を求める掃き出し法やガウス消去法とは異なり、連立方程式が唯一の解を持っていたとしても、計算が収束しなかったり、発散する場合がある。
優対角条件、つまり、
などの条件が成立しないとき、ヤコビ法などの反復法は振動したり、発散する。
このことは
の②と③を入れ換え
をヤコビ法で解かせると、このことが確かめられる。
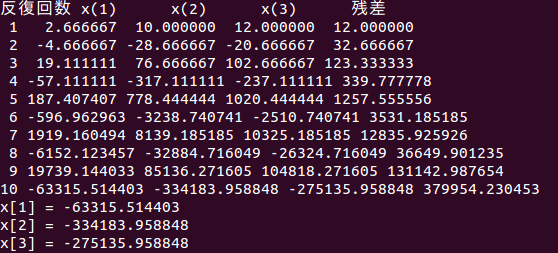
C言語によるサンプルプログラムを次に示す。
#include <math.h>
#define N 100
void Jacovi(double a[][N], double x[], double b[], int n) {
double eps = 1.e-6, sum=0, res=0;
double xn[N];
int i, j, k;
int limit = 100;
printf("反復回数 x(1) x(2) x(3) 残差\n");
for (k = 1 ; k <= limit; k++) {
res = 0;
for (i=0; i < n; i++) {
sum = b[i];
for (j=0; j < n; j++) {
sum = sum - a[i][j]*x[j];
}
res = fabs(sum);
xn[i]= x[i]+sum/a[i][i];
}
if (k%5==0) { // 5回に1度、計算途中の結果を表示
printf("%2d %10.6f %10.6f %10.6f %10.6f\n", k, xn[0],xn[1], xn[2], res);
}
for (i=0; i<n; i++) {
x[i]=xn[i];
}
if (eps>res) break;
}
}
main() {
int i, n;
double a[N][N] = {{3,1,1}, {1,3,1}, {1,1,3}};
double x[N]={0.};
double b[N]= {8., 10., 12.};
n=3;
Jacovi(a,x,b,n);
for (i = 0; i < n; i++) {
printf("x[%d] = %f\n", i+1,x[i]);
}
}
ネムネコ、表計算ソフトで、平行平板間の流れ(平板ポアズイユ流れ)を解く!! [ネコ騙し数学]
平行平板間の流れ
平行平板間の流れに関する、次の微分方程式を、表計算ソフトを使って解いてみたにゃ。
これがその結果。
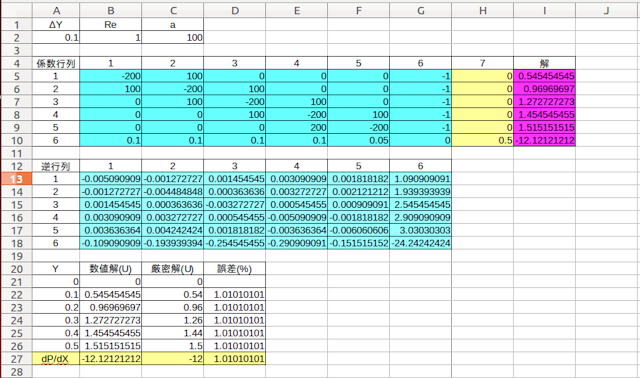
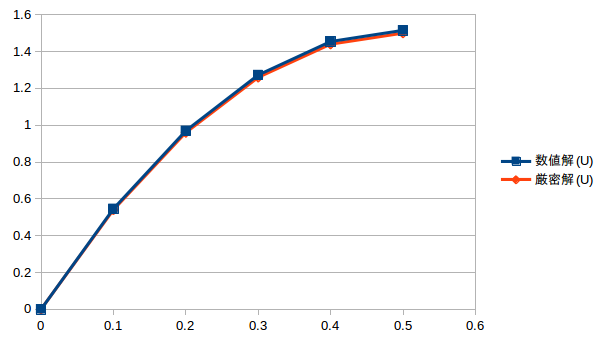
ΔY=0.1という非常に粗い分割でも、相対誤差約1%で解けてしまうだケロ。
すごいもんだろ。
ネットにスプレッドシートを公開したんで、興味のあるヒトはアクセスするといいにゃ。
LibreOffice calc版は↓
だにゃ。
平行平板間の流れ(平面ポアズイユ流れ) [ネコ騙し数学]
平行平板間の流れ(平面ポアズイユ流れ)
右図のような2つの無限平行板間の流れは、次の方程式で表される。
ここで、pは圧力、uはx軸に平行な流速、さらに、Qは(体積)流量、μは粘性係数である。
なお、(1)の境界条件は
(1)は、流体力学の基礎方程式であるナビエ・ストークス方程式
の最も簡単なものの一つで、ナビエ・ストークスの解析解(厳密解)が得られるものの一つで、平均流速
を用いると、解は
である。
u、yを
と無次元化すると、(5)式は
となり、UはY=1/2のときに
という最大値をとる。
さらに、pとxを次のように無次元化すると
(1)、(2)式は
ここで、Reはレイノルズ数と言われる、流体力学で流れを支配する、重要な無次元数で
である。
実は、このReが大きくなると、ナビエストークス方程式の非線形項の非線形性が強くなり、流れは時間、空間的に不規則――不規則って何だ(・・?――な乱流という、数学・物理学的に厄介なものになるのだけれど・・・。
それで、今回、やりたいのは、差分法を用いて、(10)と(11)を連立方程式に直し、これを数値的に解こうということ。
(7)式を見るとわかるけれど、この流れの速度分布は、Y=1/2を軸とする放物線で表されており、Y=1/2で対称である。
したがって、
だから、
(10)式の境界条件は、
ではなく、
としてもよい。
なぜ、境界条件を、(14)ではなく、(15)とするかというと、計算領域を0≦Y≦1から0≦Y≦1/2と小さくし、計算量をできるだけ少なくしたいから。
[0,1/2]をn等分し、
とおき、
とし、この点における無次元流速Uを
とする。
差分法を用いると
となるので、(10)式は
となり、
![]()
ここで、
とおけば、(19)式は
になる。
Y=0の境界条件U=0より
問題は、Y=1/2における境界条件
をどのように扱うかだけれど、中心差分を用いると、
となるので、i=nのとき
とすればよいだろう。
(11)式も対称性を利用すると、
となり、左辺の積分を台形公式で近似すれば、
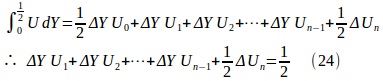
となる。
よって、
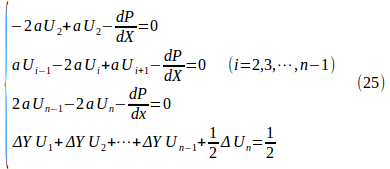
というn+1元の連立方程式が得られる。
未知数は、のn個とdP/dXの1個で、合せてn+1個だから、連立方程式(25)を解くことによって、この未知数を全て求めることができる。
(25)は行列で書き換えると、
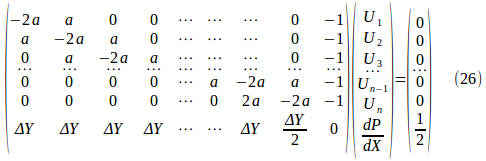
したがって、係数行列を
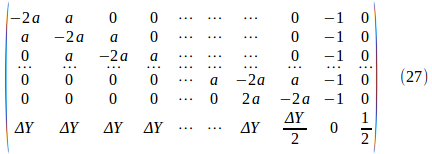
にすることにより、ガウス消去法や掃き出し法を用いて連立方程式(26)を解くことができる!!
(26)の左辺の行列の成分の圧倒的多数は0の疎行列なので、単純なガウス消去法などの直接法は無駄な計算が多く、効率的ではないのだけれど・・・。
n=10の場合の計算結果は次のとおり。
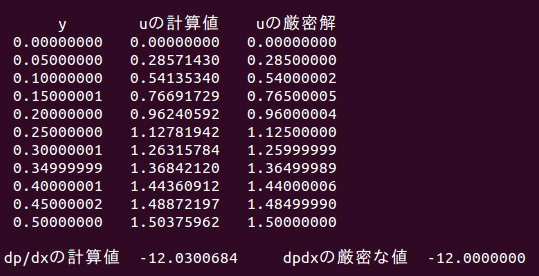
速度U、圧力勾配dP/dXの計算誤差は約0.25%に収まっていることがわかる。
実は、ここまでのプログラムを作ると、それをもとに、より複雑なNS方程式の特殊形
で表される無限平板間の流れを数知的に解くこともできる!!
なのですが、上の方程式は非線形な上に、計算点が少なくとも数百〜数千程度になるので、ガウス消去法などの直接法で、上の連立微分方程式から得られる連立方程式を解くなど狂気の沙汰!!
連立方程式
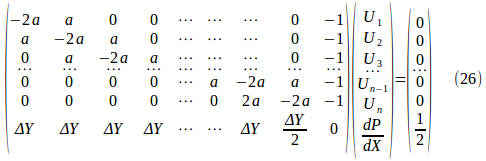
を効率よく解く数値計算法、つまり、アルゴリズムを作らないといけない。
ガウス消去法の計算量はn³程度になるという話を前にしたけれど、ガウス消去法をもとに、計算量をnオーダーに留める計算手法、アルゴリズムを作ることは可能!!
我はと思うヒトは、この計算手法を考えてみるといいにゃ。
それさえできれば、
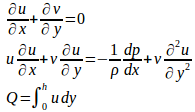
を数値的に解くプログラムを作ることだって可能になる!!
最小2乗法による近似式の決定 [ネコ騙し数学]
最小2乗法による近似式の決定
§1 最小2乗法による近似多項式の求め方
n個のデータがあるとする。
このデータがm次の多項式(m≦n+1)
に沿っているとし、
が最小になるようにm次多項式(1)の係数を定める方法を最小2乗法という。
最小2乗法では、
とおいたとき、(2)式が最小になるようにを定めるので、
にならなければならない。
したがって、
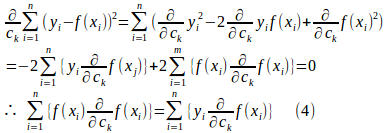
でなければならない。
ところで、
となるので、(4)式は
ここで、
とおくと、(5)式は
となる。
したがって、この連立方程式(7)を解くことによって、多項式(1)の係数を定めることができる。
特に、m=1のとき、すなわち、
のとき、(7)は
ここで、
となるので、(8)は
これを解くと、
ここで、
したがって、統計学の回帰直線と一致する。
§2 プログラム
n個のデータをもとに、最小2乗法を用いてm次の近似多項式を求める連立方程式は(6)、(7)式から与えられる。
(6)、(7)から与えられる連立方程式をガウス消去法を用いて解くことにすると、例えば、次のようなプログラムを作ることができる。
real x(20),y(20) !xとyのデータは20個まで
real c(0:10) ! 近似多項式の係数(10次まで)
real y_c(20)
data x/20*0/ ! x(i)の初期化
data y/20*0/ ! y(i)の初期化
write(6,*) "データの個数nを入力"
read(5,*) n
write(6,*) "データの入力"
read(5,*) (x(i), i=1,n) ! xのデータをn個入力
read(5,*) (y(i), i=1,n) ! yのデータをn個入力
write(6,*) "近似多項式の次数mを入力"
read(5,*) m
call lsm(x,y,n,m,c)
write(6,*)
! 近似式の係数の表示
write(6,*) "近似多項式の係数"
do i=0, m
write(6,100) 'c(',i, ')=', c(i)
end do
write(6,*)
! 計算結果
write(6,*) " x(i) y(i) 計算値"
do i= 1, n
s = 0
do j=0, m
s = s + c(j)*x(i)**j
end do
y_c(i)=s
write(6,110) x(i), y(i), s
end do
open(1,file='lsm.dat', status='replace')
do i=1,n
write(1,120) x(i),y(i),y_c(i)
end do
100 format(a,i2,a3,f10.7)
110 format(f10.7,2x,f10.7,2x,f10.7)
120 format(f10.7,x,f10.7,x,f10.7)
end
! ここから下は変えないほうがよい(^^)
! 最小二乗法
subroutine lsm(x,y,n,m,c)
real a(0:50,0:51)
real x(20), y(20), c(0:10)
real s(0:20), t(0:10)
! 係数の初期化
do i=0, 2*m
s(i) = 0
end do
do i=0, m
t(i)=0;
end do
! 係数を計算
do i=1, n
do j=0, 2*m
s(j) = s(j)+x(i)**j
end do
do j=0, m
t(j)= t(j)+x(i)**j * y(i)
end do
end do
! 係数行列に値をセット
do i= 0, m
do j=0, m
a(i,j) = s(i+j)
end do
a(i,m+1) = t(i)
end do
! ガウス消去法で連立方程式を解く
call Gauss(a,m)
do i=0, m
c(i) = a(i,m+1)
end do
end
subroutine Gauss(a,n) ! ガウス消去法
real a(0:50,0:51)
! foward marching process
do k=0, n-1
! ピボット選択
i_max = k
do j=k+1, n
if (abs(a(k,i_max)).lt.abs(a(k,j))) i_max = j
end do
if (i_max.ne.k) then
do j=k,n+1
w=a(i_max, j)
a(i_max, j) = a(k,j)
a(k,j) = w
end do
det=-det
end if
if (abs(a(k,k)).lt.eps) then
det =0.
return
end if
! ピボット選択終わり
do i=k+1, n
t=a(i,k)/a(k,k)
do j=k+1, n+1
a(i,j)=a(i,j)-t*a(k,j)
end do
end do
end do
! backward marching process
do i=n,0, -1
d = a(i,n+1)
do j= n, i+1, -1
d=d- a(i,j)*a(j,n+1)
end do
a(i,n+1)=d/a(i,i)
end do
end
たとえば、次の3個のデータ
(1,1) , (2,5), (3,8)
をもとに2次の近似多項式を求めると、次のようになる。
さらに、次の7個のデータ
(−3,5),(−2,−2),(−1,−3),(0,−1),(1,1)、(2,4),(3,5)
をもとに5次の近似多項式を求めると、次のようになる。
[境界要素法プログラムを設計する(計算部と出力部の実装)] [ネコ騙し数学]
1.実行者は要素だ。そして常にトップダウンだ!
入力部の実装によって、計算に必要な全ての情報はセットされました(されたはず(^^;))。次にやる事は、それらを利用して具体的な計算ルーティンを書く事です。計算部(ビジネスルール層)は、アプリケーションの中で最も動的な部分で、書いてて最も面白い部分でもありますが、バグの温床にもなります。最も動的だからです。
人間は動的対象を見るとすぐに幻惑され、目算を見失います。なので動的過程を動かす、メタな静的構造を保持しておくのが安全です。それは多くの場合、動的過程の制御部分ですが、これとトップダウン思考を重ねると、制御部分は「実行者」になります。「実行者」は「要素」でした。
[計算部]の冒頭にこうあります。
REM 境界要素番号kで境界積分を行うLoop
REM 要素番号kからEN_B(k,2)に従い節点を特定し、要素ごとに境界積分を実行
REM 上記結果に基づき、係数マトリックスBとHを作成
要するにLoopを作りますが、設計の基本は常トップダウンです。よってLoopは、最外殻から書き始めるのが基本です。そうして動的過程を動かすメタな静的構造を確定させると、そこに「実行者」がすんなり納まります。要するに、境界要素を走るLoopを最初に書くべきだ、という事です。
REM 境界要素番号kで境界積分を行うLoop
For k = 1 to B_Count
REM 要素番号kからEN_B(k,2)に従い節点を特定し、要素ごとに境界積分を実行
REM 上記結果に基づき、係数マトリックスBとHを作成
Next k
ところで上記を見て、何か気づきませんか?。目標とする方程式系は、
そこで慌てて[メモ欄]を見返すと、定義してない!。[メモ欄]と[宣言部]は一対一に対応してるので、要はAを宣言してないって事です。そこでさらに慌てて、[メモ欄]のz(i)に関する部分の後に、
REM A(i, j):全体係数マトリックス、i,j=1~2*BN_Count
と書き加え同時に、[宣言部]の同じ場所に、
Dim A(1000, 1000) REM 全体係数マトリックス、i,j=1~2*BN_Count
を追加します。i,j=1~2*BN_Countなのは、z(i),i=1~2*BN_Countだからです。
実務でもこんな事は良くあるのだ!。じっさい忘れてたし(^^;)。でもトップダウン方式だから被害は最小限と思えませんか?。これがボトムアップだったら、既に変数Aは別の目的で使われてて2重宣言が起こり、いや2度ある事は3度ある・・・3重宣言が起こり、3つあるAの内の2つをA1とA2に書き変える事にして、沢山の行のAを一つ一つ判断しながらA1やA2に書き変え、そこでまた判断ミスしてそれがまたバグの温床となり、・・・で訳わかんなくなってバグの連鎖反応が、・・・などと屁理屈をこねるのであった(^^;)。
全体係数マトリックスAを導入したおかげで、さらにもう一つの大事に気づきます。思い起こせば境界積分の値は、特異点の位置によって変わるのでした。マトリックスAは境界方程式に対応するので、いま考える特異点は境界節点のどれかと一致します。その番号(特異点番号)をiとした時、iはAに含まれるBとHの行番号なのでした。つまり、
REM 境界要素番号kで境界積分を行うLoop
For i = 1 to BN_Count
REM 特異点番号iの節点iを特定
For k = 1 to B_Count
REM 要素番号kからEN_B(k,2)に従い節点を特定し、要素ごとに境界積分を実行
REM 上記結果に基づき、係数マトリックスBとHを作成
Next k
Next i
としなければならない訳です。まぁ~、こういう事も良くありますって・・・(^^;)。
次にもう少し「境界要素番号kで境界積分を行うLoop」を具体化します。入力部の情報をいかに使うべきかを、自分にわからせるためにです。
REM 境界要素番号kで境界積分を行うLoop
For i = 1 to BN_Count
REM 特異点番号iの節点iを特定
x0 = BN(i, 1) REM 節点iの(x,y)座標
y0 = BN(i, 2)
For k = 1 to B_Count
REM 要素番号kからEN_B(k,2)に従い節点を特定し、要素ごとに境界積分を実行
j1 = EN_B(k,1) REM 要素kの始端の節点番号
j2 = EN_B(k,2) REM 要素kの終端の節点番号
x1 = BN(j1, 1) REM 節点j1の(x,y)座標
y1 = BN(j1, 2)
x2 = BN(j2, 1) REM 節点j2の(x,y)座標
y2 = BN(j2, 2)
REM (x0,y0),(x1,y1),(x2,y2)から、要素kの境界積分値を計算
REM ψj1に関する結果をB1,qj1に関する結果をH1で表す
REM ψj2に関する結果をB2,qj2に関する結果をH2で表す
REM 上記結果に基づき、係数マトリックスBとHを作成
jj1 = BN_Z(j1,1) REM ψj1の解ベクトルzの中での位置
jjj1 = BN_Z(j1,2) REM qj1の解ベクトルzの中での位置
jj2 = BN_Z(j2,1) REM ψj2の解ベクトルzの中での位置
jjj2 = BN_Z(j2,2) REM qj2の解ベクトルzの中での位置
A(i, jj1) = A(i, jj1) - B1
A(i, jjj1) = A(i, jjj1) + H1
A(i, jj2) = A(i, jj2) - B2
A(i, jjj2) = A(i, jjj2) + H2
Next k
Next i
赤字の部分はいま追加したコメントで、後で考える必要のある部分です。
「A(i, jj1) = A(i, jj1) - B1」などの部分は、次の理由によります。一つの特異点iについて境界積分は具体的には、次の形になりました。
(ξi,ηi)を番号(節点番号)iの特異点だとして、
A(i, jj1) = A(i, jj1) - B1
A(i, jj2) = A(i, jj2) - B2
などとしとけば良いじゃん!、という話です。こうしとけば、「For k = 1 to B_Count」のLoopを回しただけで、自然に要素kとk+1に関する「重ね合わせ(足し算)」が起きるからです。そのためにこそ、要素-節点番号対応表EN_B(k,2)があるんですよ。
※ 宣言時にA(i, j)は、自動で全ての値が0に初期化されるのが普通です。
有限要素法などだと少なくとも2次元なので、要素-節点番号対応表がないとプログラムすら書けません。要素-節点番号対応表は、2次元領域を有限要素分割して初めて決まります。そういう訳でメッシュ切り(有限要素分割)と要素-節点番号対応表の生成は、FEMの中で最も手のかかる作業なんです、現実には(^^;)。
とりあえず境界方程式の核心部分は、これで生成できるはずです。次へ進みましょう。次には、
REM 領域要素番号kで領域積分を行うLoop
REM 要素番号kからEN_R(k,4)に従い節点を特定し、要素ごとに領域積分を実行
REM 上記結果に基づき、既知ベクトルwを作成
と書いてあります。念のため次の事を注意します。
これから最後のREM文に書いてある既知ベクトルwをセットする事になりますが、wの値は解ベクトル(未知ベクトル)zへセットします。これは連立方程式プログラムでは普通に行われる事で、係数マトリックスAと既知ベクトルとしてのzを連立方程式の解法部(たいていサブルーティン)へ送ると、zに解がセットされて返って来る仕掛けになるからです。こうすると既知ベクトル分のメモリを節約できます。
ここも基本は同じです。
REM 領域要素番号kで領域積分を行うLoop
For i = 1 to BN_Count
REM 特異点番号iの節点iを特定
h = 0
For k = 1 to R_Count
REM 要素番号kからEN_R(k,4)に従い節点を特定し、要素ごとに領域積分を実行
REM 特異点iと要素節点情報から積分値w0を計算
h = h + w0
Next k
REM 上記結果に基づき、既知ベクトルwを作成
z(i) = h
Next i
領域積分項wは、ラプラス方程式Δψ=gの既知関数g(x,y)に対応するものですが、今回g(x,y)は具体的に与えてないので、領域積分についてはこれ以上具体化しません。プログラムテストのところで、いくつか具体的例を出す予定です。
これで離散化された境界方程式はセットされました(されたはず(^^;))。残りは境界条件のセットです。
REM 境界節点番号jで境界条件位置を指定するLoop
REM 節点番号jからBN_BP(j,2)とBN_Z(j,2) に従い、(D1 D2)ブロックを作成
REM 節点番号jに従いBN_BV(j,2)の値をwブロックの後に並べ、(d1 d2)ブロックを作成
・・・なんですが、既に最外殻Loopは、全体係数マトリックスAの行番号iに関するものなのがわかっています。境界条件は境界方程式に対する補助条件なので、Aの中で境界方程式の行並びの後に、単純に並べれば良いだけです。境界方程式の行並びは特異点番号に一致し、それは特異点が境界節点のどれかと一致する事を表す並びでもあったので、境界方程式の行並びの行番号はi = 1~BN_Countでした。境界条件の行並びはi = BN_Count + 1から始まります。境界条件は1個の境界節点に必ず1個あります。従って、
REM 境界節点番号jで境界条件位置を指定するLoop
For i = BN_Count + 1 to 2 * BN_Count
REM 節点番号jからBN_BP(j,2)とBN_Z(j,2) に従い、(D1 D2)ブロックを作成
REM 節点番号jに従いBN_BV(j,2)の値をwブロックの後に並べ、(d1 d2)ブロックを作成
Next i
いまLoop内のREM文の中の節点番号jは、さっきの説明から、j=i-BN_Countです。そこに注意すると、
※「十進BASIC 最新版 概要」によると、IFブロックが使えます。
http://hp.vector.co.jp/authors/VA008683/basic02.htm
REM 境界節点番号jで境界条件位置を指定するLoop
For i = BN_Count + 1 to 2 * BN_Count
REM 行番号から節点番号を特定する
j = i - BN_Count
REM 節点番号jからBN_BP(j,2)とBN_Z(j,2) に従い、(D1 D2)ブロックを作成
REM 節点番号jに従いBN_BV(j,2)の値をwブロックの後に並べ、(d1 d2)ブロックを作成
If BN_BP(j,1) = 1 Then
REM ψjが既知が場合
jj = BN_Z(j,1) REM ψjの解ベクトルzの中での位置
A(i, jj) = 1 REM ψjの値を与えるので、Aの成分は1
z(i) = BN_BV(jj,1) REM ψjの値
ElseIf BN_BP(j,2) = 1 Then
REM qjが既知が場合
jj = BN_Z(j,2) REM qjの解ベクトルzの中での位置
A(i, jj) = 1 REM qjの値を与えるので、Aの成分は1
z(i) = BN_BV(jj,2) REM qjの値
End If
Next i
IFブロックを書く時もトップダウンの作法に従い、まずIf~ElseIf~End Ifのブロックの形を決めてから、必要なら説明のためのREM分をブロック内に書き込み、最後に具体的なコードを書く事をお奨めします。
最後に、全体係数マトリックスAと既知ベクトルとしてのzを連立方程式の解法部へ送ります。
REM 全体係数行列が出来たので、Gaussの掃き出し法にかけ、未知ベクトルzを求める
これも後で考えるべきものとして、赤字化しておきます。
[出力部]は短いので、それもここでやってしまいましょう。
REM BN_Z(j,2) に従いz(j)から値を読み出し、出力
For j = 1 to BN_Count
jj = BN_Z(j,1) REM zの中でのψjの位置
REM z(jj)をψjの出力ルーティンへ渡す
Next i
For j = 1 to BN_Count
jj = BN_Z(j,2) REM zの中でのqjの位置
REM z(jj)をqjの出力ルーティンへ渡す
Next i
赤字の部分は、サブルーティン化する予定です。でもその前に、本当にサブルーティン化する必要があるのか?を検討して、損はありません。
REM [メモ欄]
REM B_Count:境界要素数
REM EN_B(k,2):境界要素-節点対応表,k=1~B_Count
REM (k,1):要素kの始端の節点No.,(k,2):終端の節点No.
REM R_Count:領域要素数
REM EN_R(k,4):領域要素-節点対応表,k=1~R_Count
REM (k,j),j=1~4:jに従って要素kの要素節点No.を左回りに格納
REM BN_Count:境界節点数
REM BN(j,2):境界節点座標,j=1~BN_Count,(j,1):節点jのx座標,(j,2):y座標
REM RN_Count:領域節点数
REM RN(j,2):領域節点座標,j=1~RN_Count,(j,1):節点jのx座標,(j,2):y座標
REM BN_BP(j,2):節点の境界条件の有無,j=1~BN_Count
REM (j,1):節点jのψjが既知なら1、そうでないなら0
REM (j,2):節点jのqjが既知なら1、そうでないなら0
REM BN_BV(j,2):境界条件の値,j=1~BN_Count
REM (j,1):節点jのψjに与える値
REM (j,2):節点jのqjに与える値
REM z(i):未知ベクトル,i=1~2*BN_Count
REM BN_Z(j,2):節点-未知数対応表,j=1~BN_Count
REM (j,1):ψjのzの中の位置,(j,2):qjのzの中の位置
REM 節点j→ψj→z(j),節点j→qj→z(BN_Count+j)
REM A(i, j):全体係数マトリックス、i,j=1~2*BN_Count
REM [宣言部]
REM 配列寸法の上限は1000
REM B_Count:境界要素数
REM R_Count:領域要素数
Dim EN_B(1000,2) REM 境界要素-節点対応表,k=1~B_Count
Dim EN_R(1000,4) REM 領域要素-節点対応表,k=1~R_Count
REM BN_Count:境界節点数
REM RN_Count:領域節点数
Dim BN(1000,2) REM 境界節点座標,j=1~BN_Count
Dim RN(1000,2) REM 領域節点座標,j=1~RN_Count
Dim BN_BP(1000,2) REM 節点の境界条件の有無,j=1~BN_Count
Dim BN_BV(1000,2) REM 境界条件の値,j=1~BN_Count
Dim BN_Z(1000,2) REM 節点-未知数対応表,j=1~BN_Count
Dim z(1000) REM 未知ベクトル,i=1~2*BN_Count
Dim A(1000, 1000) REM 全体係数マトリックス、i,j=1~2*BN_Count
REM [入力部]
REM境界要素数B_Countと領域要素数R_Countは、事前に与えられると仮定する。
REM 境界要素と領域要素データは、要素ごとに節点番号が与えられると仮定する。
REM 与えられる節点番号は、左回りに順序付けられたものが与えられると仮定する。
REM 境界要素を要素番号kで読み込むLoop
REM Loop内で要素ごとの節点番号を読み、境界要素-節点対応表EN_B(k,2)をセット
For k = 1 to B_Count
EN_B(k,1) = ?
EN_B(k,2) = ?
Next k
REM 領域要素を要素番号kで読み込むLoop
REM Loop内で要素ごとの節点番号を読み、領域要素-節点対応表EN_R(k,4)をセット
For k = 1 to R_Count
For j = 1 to 4
EN_R(k,j) = ?
Next j
Next k
REM境界節点数BN_Countと領域節点数RN_Countは、事前に与えられると仮定する。
REM 境界節点を節点番号jで読み込むLoop
REM Loop内で境界節点座標を読み、BN(j,2)をセット
For j = 1 to BN_Count
BN(j,1) = ?
BN(j,2) = ?
Next j
REM 領域節点を節点番号jで読み込むLoop
REM Loop内で領域節点座標を読み、RN(j,2)をセット
For j = 1 to RN_Count
RN(j,1) = ?
RN(j,2) = ?
Next j
REM 境界条件の場所を節点番号jで読み込むLoop
REM Loop内で節点jの境界条件の有無を読み、BN_BP(j,2)をセット
For j = 1 to BN_Count
BN_BP(j,1) = ?
BN_BP(j,2) = ?
Next j
REM 境界条件の値を節点番号jで読み込むLoop
REM Loop内で節点jの境界条件の値を読み、BN_BV(j,2)をセット
For j = 1 to BN_Count
BN_BV(j,1) = ?
BN_BV(j,2) = ?
Next j
REM 節点番号jのLoopで、節点-未知数対応表BN_Z(j,2)をセット
REM (j,1):ψjのzの中の位置,(j,2):qjのzの中の位置
REM 対応は、節点j→ψj→z(j),節点j→qj→z(BN_Count+j)
For j = 1 to BN_Count
BN_Z(j,1) = j
BN_Z(j,2) = BN_Count + j
Next j
REM [計算部]
REM 境界要素番号kで境界積分を行うLoop
For i = 1 to BN_Count
REM 特異点番号iの節点iを特定
x0 = BN(i, 1) REM 節点iの(x,y)座標
y0 = BN(i, 2)
For k = 1 to B_Count
REM 要素番号kからEN_B(k,2)に従い節点を特定し、要素ごとに境界積分を実行
j1 = EN_B(k,1) REM 要素kの始端の節点番号
j2 = EN_B(k,2) REM 要素kの終端の節点番号
x1 = BN(j1, 1) REM 節点j1の(x,y)座標
y1 = BN(j1, 2)
x2 = BN(j2, 1) REM 節点j2の(x,y)座標
y2 = BN(j2, 2)
REM (x0,y0),(x1,y1),(x2,y2)から、要素kの境界積分値を計算
REM ψj1に関する結果をB1,qj1に関する結果をH1で表す
REM ψj2に関する結果をB2,qj2に関する結果をH2で表す
REM 上記結果に基づき、係数マトリックスBとHを作成
jj1 = BN_Z(j1,1) REM ψj1の解ベクトルzの中での位置
jjj1 = BN_Z(j1,2) REM qj1の解ベクトルzの中での位置
jj2 = BN_Z(j2,1) REM ψj2の解ベクトルzの中での位置
jjj2 = BN_Z(j2,2) REM qj2の解ベクトルzの中での位置
A(i, jj1) = A(i, jj1) - B1
A(i, jjj1) = A(i, jjj1) + H1
A(i, jj2) = A(i, jj2) - B2
A(i, jjj2) = A(i, jjj2) + H2
Next k
Next i
REM 領域要素番号kで領域積分を行うLoop
For i = 1 to BN_Count
REM 特異点番号iの節点iを特定
h = 0
For k = 1 to R_Count
REM 要素番号kからEN_R(k,4)に従い節点を特定し、要素ごとに領域積分を実行
REM 特異点iと要素節点情報から積分値w0を計算
h = h + w0
Next k
REM 上記結果に基づき、既知ベクトルwを作成
z(i) = h
Next i
REM 境界節点番号jで境界条件位置を指定するLoop
For i = BN_Count + 1 to 2 * BN_Count
REM 行番号から節点番号を特定する
j = i - BN_Count
REM 節点番号jからBN_BP(j,2)とBN_Z(j,2) に従い、(D1 D2)ブロックを作成
REM 節点番号jに従いBN_BV(j,2)の値をwブロックの後に並べ、(d1 d2)ブロックを作成
If BN_BP(j,1) = 1 Then
REM ψjが既知が場合
jj = BN_Z(j,1) REM ψjの解ベクトルzの中での位置
A(i, jj) = 1 REM ψjの値を与えるので、Aの成分は1
z(i) = BN_BV(jj,1) REM ψjの値
ElseIf BN_BP(j,2) = 1 Then
REM qjが既知が場合
jj = BN_Z(j,2) REM qjの解ベクトルzの中での位置
A(i, jj) = 1 REM qjの値を与えるので、Aの成分は1
z(i) = BN_BV(jj,2) REM qjの値
End If
Next i
REM 全体係数行列が出来たので、Gaussの掃き出し法にかけ、未知ベクトルzを求める
REM [出力部]
REM BN_Z(j,2) に従いz(j)から値を読み出し、出力
For j = 1 to BN_Count
jj = BN_Z(j,1) REM zの中でのψjの位置
REM z(jj)をψjの出力ルーティンへ渡す
Next i
For j = 1 to BN_Count
jj = BN_Z(j,2) REM zの中でのqjの位置
REM z(jj)をqjの出力ルーティンへ渡す
Next i
[境界要素法プログラムを設計する(入力部の実装)] [ネコ騙し数学]
[境界要素法プログラムを設計する(入力部の実装)]
1.なぜ入力部からなのか?
なぜ入力部から作るんでしょうか?。開発環境のコンパイラーにしてみれば、エラーが出ない限り、どっから手を付けられたってオッケーなはずです。だからこれは、人間の都合なんですよ。
一つは[入力部]→[計算部]→[出力部]の順に作って行くと、プログラムが完成した暁の実際の動作をプログラミング中にシミュレートする事になり、人間としては大変に考えやすい(^^)。
二つ目はテストのやりやすさです。[入力部]→[計算部]と作って行けば、[計算部]が上がった時点で一応のテストが可能になります。「開発サイクルは出来るだけ短く」です(^^)。それに一番間違えやすそうなのは、[計算部]に決まってます。[計算部]はできるだけ早くテストしたいし、ここがほとんどプログラムの核心です。そのテストの具合によっては[入力部]の仕様変更だってありえます。
以上は三層開発モデルの考え方に近いです。そこでは[入力部],[計算部],[出力部]は、[インターフェイス層],[ビジネスルール層],[データベース層]と難しそうに名を変えますが、結局やる事は同じなんですよ。
オブジェクトプログラミングの基本作法とか称して、三層開発モデルみたいな小難しいものに出会った事があるかも知れませんが、言ってる事はものすごく当たり前の事です。当たり前の事を誰も素直にやろうとしないから、そういう開発モデルが提唱されただけなんです。それはISOも同じです(^^;)。
余談ですが業務アプリの開発では、[入力部],[計算部],[出力部]を同時並行に開発する事もあります。エッ?できるの?って気もしますが(^^;)、例えば[計算部]にとって[入力部]は一種の外部環境です。そこでモックと呼ばれる仮想オブジェクトを作り、[入力部]の仕様をモックでシミュレートして[入力部]が作ったかのような外部データを[計算部]に渡しテストする訳です。ただこれは、相当な金と時間とマンパワー(と優秀な人材)がないと、ほとんど実現不可能です。ここではやらないのが無難ですな(^^;)。
ちなみにプログラムを書くことを実装と言います。実装で行われる作業全体の事を製造と言ったりします。
2.入力部の実装
前回の[メモ欄]と[宣言部]を参照しつつ、[入力部]の冒頭に書いてある事を読みます。その冒頭には、
REM境界要素数B_Countと領域要素数R_Countは、事前に与えられると仮定する。
REM 境界要素と領域要素データは、要素ごとに節点番号が与えられると仮定する。
REM 与えられる節点番号は、左回りに順序付けられたものが与えられると仮定する。
とあり、その直後には、
REM 境界要素を要素番号kで読み込むLoop
REM Loop内で要素ごとの節点番号を読み、境界要素-節点対応表EN_B(k,2)をセット
とあります。
いま本当に具体的な入力ルーティンは書けないのですが、最初の仮定通りのものが既にあるのなら、EN_B(k,2)のセットは、以下です。ただし代入文のLETは省略してます(面倒なので)。後で補充して下さい(^^;)。
For k = 1 to B_Count
EN_B(k,1) = ?
EN_B(k,2) = ?
Next k
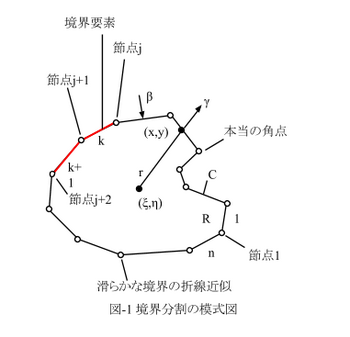
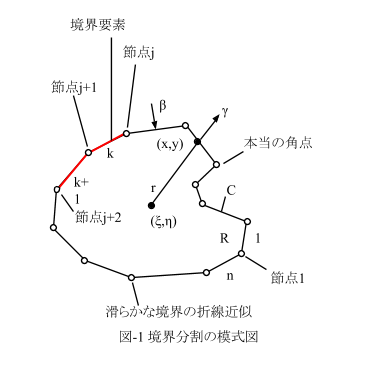
となります。ここで「?」は、最初の仮定により与えられる値です。でも図-1を見れば、EN_B(k,1) = k,EN_B(k,2) = k+1,k = B_Countの時はEN_B(k,2) = 1、ってのがわかります。こういう風に与えてもOKなんですが個人的には、事前にちゃんと「?」のデータを作る事をお奨めします。
次の、
REM 領域要素を要素番号kで読み込むLoop
REM Loop内で要素ごとの節点番号を読み、領域要素-節点対応表EN_R(k,4)をセット
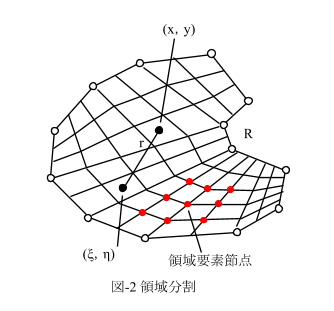
も同様です。これは図-2のように、領域要素が4角形要素を想定したケースです。
For k = 1 to R_Count
For j = 1 to 4
EN_R(k,j) = ?
Next j
Next k
後も同様なので、直接[入力部]にコードを書き込んで、今回は終了します。
REM [メモ欄]
REM B_Count:境界要素数
REM EN_B(k,2):境界要素-節点対応表,k=1~B_Count
REM (k,1):要素kの始端の節点No.,(k,2):終端の節点No.
REM R_Count:領域要素数,Region Elements Countの略
REM EN_R(k,4):領域要素-節点対応表,k=1~R_Count
REM (k,j),j=1~4:jに従って要素kの要素節点No.を左回りに格納
REM BN_Count:境界節点数
REM BN(j,2):境界節点座標,j=1~BN_Count,(j,1):節点jのx座標,(j,2):y座標
REM RN_Count:領域節点数
REM RN(j,2):領域節点座標,j=1~RN_Count,(j,1):節点jのx座標,(j,2):y座標
REM BN_BP(j,2):節点の境界条件の有無,j=1~BN_Count
REM (j,1):節点jのψjが既知なら1、そうでないなら0
REM (j,2):節点jのqjが既知なら1、そうでないなら0
REM BN_BV(j,2):境界条件の値,j=1~BN_Count
REM (j,1):節点jのψjに与える値
REM (j,2):節点jのqjに与える値
REM z(i):未知ベクトル,i=1~2*BN_Count
REM BN_Z(j,2):節点-未知数対応表,j=1~BN_Count
REM (j,1):ψjのzの中の位置,(j,2):qjのzの中の位置
REM 節点j→ψj→z(j),節点j→qj→z(BN_Count+j)
REM [宣言部]
REM 配列寸法の上限は1000
REM B_Count:境界要素数
REM R_Count:領域要素数
Dim EN_B(1000,2) REM 境界要素-節点対応表,k=1~B_Count
Dim EN_R(1000,4) REM 領域要素-節点対応表,k=1~R_Count
REM BN_Count:境界節点数
REM RN_Count:領域節点数
Dim BN(1000,2) REM 境界節点座標,j=1~BN_Count
Dim RN(1000,2) REM 領域節点座標,j=1~RN_Count
Dim BN_BP(1000,2) REM 節点の境界条件の有無,j=1~BN_Count
Dim BN_BV(1000,2) REM 境界条件の値,j=1~BN_Count
Dim BN_Z(1000,2) REM 節点-未知数対応表,j=1~BN_Count
Dim z(1000) REM 未知ベクトル,i=1~2*BN_Count
REM [入力部]
REM境界要素数B_Countと領域要素数R_Countは、事前に与えられると仮定する。
REM 境界要素と領域要素データは、要素ごとに節点番号が与えられると仮定する。
REM 与えられる節点番号は、左回りに順序付けられたものが与えられると仮定する。
REM 境界要素を要素番号kで読み込むLoop
REM Loop内で要素ごとの節点番号を読み、境界要素-節点対応表EN_B(k,2)をセット
For k = 1 to B_Count
EN_B(k,1) = ?
EN_B(k,2) = ?
Next k
REM 領域要素を要素番号kで読み込むLoop
REM Loop内で要素ごとの節点番号を読み、領域要素-節点対応表EN_R(k,4)をセット
For k = 1 to R_Count
For j = 1 to 4
EN_R(k,j) = ?
Next j
Next k
REM境界節点数BN_Countと領域節点数RN_Countは、事前に与えられると仮定する。
REM 境界節点を節点番号jで読み込むLoop
REM Loop内で境界節点座標を読み、BN(j,2)をセット
For j = 1 to BN_Count
BN(j,1) = ?
BN(j,2) = ?
Next j
REM 領域節点を節点番号jで読み込むLoop
REM Loop内で領域節点座標を読み、RN(j,2)をセット
For j = 1 to RN_Count
RN(j,1) = ?
RN(j,2) = ?
Next j
REM 境界条件の場所を節点番号jで読み込むLoop
REM Loop内で節点jの境界条件の有無を読み、BN_BP(j,2)をセット
For j = 1 to BN_Count
BN_BP(j,1) = ?
BN_BP(j,2) = ?
Next j
REM 境界条件の値を節点番号jで読み込むLoop
REM Loop内で節点jの境界条件の値を読み、BN_BV(j,2)をセット
For j = 1 to BN_Count
BN_BV(j,1) = ?
BN_BV(j,2) = ?
Next j
REM 節点番号jのLoopで、節点-未知数対応表BN_Z(j,2)をセット
REM (j,1):ψjのzの中の位置,(j,2):qjのzの中の位置
REM 対応は、節点j→ψj→z(j),節点j→qj→z(BN_Count+j)
For j = 1 to BN_Count
BN_Z(j,1) = j
BN_Z(j,2) = BN_Count + j
Next j
REM [計算部]
REM 境界要素番号kで境界積分を行うLoop
REM 要素番号kからEN_B(k,2)に従い節点を特定し、要素ごとに境界積分を実行
REM 上記結果に基づき、係数マトリックスBとHを作成
REM 領域要素番号kで領域積分を行うLoop
REM 要素番号kからEN_R(k,4)に従い節点を特定し、要素ごとに領域積分を実行
REM 上記結果に基づき、既知ベクトルwを作成
REM 境界節点番号jで境界条件位置を指定するLoop
REM 節点番号jからBN_BP(j,2)とBN_Z(j,2) に従い、(D1 D2)ブロックを作成
REM 節点番号jに従いBN_BV(j,2)の値をwブロックの後に並べ、(d1 d2)ブロックを作成
REM 全体係数行列が出来たので、Gaussの掃き出し法にかけ、未知ベクトルzを求める
REM [出力部]
REM BN_Z(j,2) に従いz(j)から値を読み出し、出力
(執筆 ddt³さん)
[境界要素法プログラムを設計する(アウトライン)] [ネコ騙し数学]
[境界要素法プログラムを設計する(アウトライン)]
1.開発範囲の決定
これは業務アプリの開発で言えば、顧客がどこまでの成果品を望むか?です。顧客の要求は常にドンダケ~なんですが、開発側としては出来るだけ簡単なものにしたい訳です(仕事したくないから(^^;))。今回の顧客は我々です。つまり開発者です。なので今回は、開発側の事情最優先です(^^)。
境界要素法プログラムの目的は、離散化された境界方程式、
を作る事にほぼ尽きます。しかし(1)はそのままでは解けないのでした。以下の条件を考慮する必要がありました。
[1]境界条件
これは、未知ベクトルψ,qの一部に値を与える補助方程式として実装するのが簡単でした。
[2]角点の処理
これは角点を表す節点jのqjが、qj(1),qj(2)と2つになり、qの成分数が増える事を意味します。それに伴い補助条件の追加も必要でした。しかも追加の仕方は、境界条件の与えられ方により変化しました。
最初から[2]を扱うと面倒そうです。例えば(1)+[1]だけなら、組み立てる連立方程式の形は、
になります。(D1 D2)ブロックは、境界条件で値を与えられる節点番号の列成分が1で、他は全て0の行列です。(d1 d2)tブロックは与える値のベクトルです。
ψとqの成分は、節点jのψjとqjを表しますが、z=(ψ q)tと一つの未知ベクトルとしてまとめると、qjのjとz上での成分番号が、既にこの時点でずれます。幸いψとqの成分数は同じなので、それをnとして、
節点j→ψj→z(j),節点j→qj→z(n+j) (3)
ではあります。z(j)などは、配列zのj成分の意味で使ってます。
これに[2]が加わると、qの成分数が角点が現れるたびに増え、(3)程度の対応ではすまなくなります。当然HとD2の列数も増え、どう増えるかなどを制御しなければなりません。さらにここに新たに補助方程式が加わりますが、加え方は一定ではないのでした。
やっぱり最初は(1)+[1]ですよね?。(1)+[1]のプログラムをテストして動作確認し、自信を持って複雑そうな[2]に進むのが妥当です。(1)+[1]の基本が出来れば、[2]への対処のポイントも絞れるはずです。要するに適切な実践に勝る教師なし!です。
もう一つ考慮すべきは、テストの容易さです。作ったプログラムは必ずテストしなければなりません。例えば全部作ってから動かなかったら、バグの特定にも難儀します。その時に「(1)+[1]まではOKよ」という事実があると、格段に楽になります。
業務アプリの開発でも、開発サイクルを出来るだけ短く区切って頻繁にテストし、より複雑な段階へ進む事が推奨されアジャイル開発と言います。その際、個々の開発サイクルでの成果は一つの製品であり、次の段階はその拡張仕様という見方をします。
2.大枠決め
「実践に勝る教師なし!」なんて言うものだから、すぐにプログラムをボトムアップで作成しようします。気持ちはわかります。ボトムアップ方式なら具体的な数式なんかを、どんどん書いて行けるので。でも「適切な」実践ですからね。開発の基本は常にトップダウンです。
プログラムの目的から始まって、何をやりたいか?何をやるべきか?のアウトラインをトップダウンで決めます。それを詳細化して行くと、局所的なボトムアップ作業へと自然につながります。こうすると常に全体を見渡しながら局所的な具体化作業に集中できます。こうすると「後で考えれば明らかだったよなぁ~」みたいな不用意で不必要なバグは激減します。
もう一つ大事なのは、トップダウン中の方針決定には、必ず明確な理由がある事。プログラム作成は、何をやろうと一長一短。すると局所的な便利さ不便さから、大域的な方針まで変更したくなります。その時、変更するのか我慢すべきか判断が必要です。全体系の整合性を保つ判断根拠になるのが、明確な決定理由です。
 自分は一時期アプリ開発で飯を食ってたので、プロの言葉は信じて良いですよぉ~(←ほんとか?(^^;))。
自分は一時期アプリ開発で飯を食ってたので、プロの言葉は信じて良いですよぉ~(←ほんとか?(^^;))。
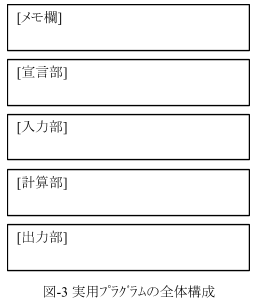
まず実用的なプログラムの全体構成は一個しかありません。図-3です。これ以外ないですよね?。ここで問題になるのは[メモ欄]だと思いますが、これは必須です。ここにプログラムの仕様を書いて行きます。[メモ欄]を読めば、全体を見渡せるように書きます。これを怠ると、たいてい後でこっぴどい目に合います。
トップダウン思考でキーになるのが、「実行者をさがせ!」です。特定された実行者が、プログラムを動かすと考えて下さい。このプログラムの目的である式(2)を見てみます。
(D1 D2)と(d1 d2)tの部分は、どうやら値を並べるだけなのでどうとでもなりそうです。対して(B H)と(w)tの部分は、今までやってきた積分式を使うべきところです。
BやHは境界積分の項です。境界積分は個々の境界要素の境界節点を特定し、主に節点情報に基づいて積分値を得た後、それを全ての要素について足すのでした。その足し算を、行列という省略記法で書いたものがB,Hです。
wは領域積分項です。同様に、領域要素の節点を特定し節点情報に基づいて積分値を得た後、それを全ての要素について足します。
自分は、このプログラムの実行者は「要素」だと思います。
境界要素や領域要素は具体的には節点で定義されます。しかし図-1,2に示すように、同じ節点が隣の要素(一つとは限らない)に共有されたりします。従って要素-節点対応表が必要です。こんな具合です。
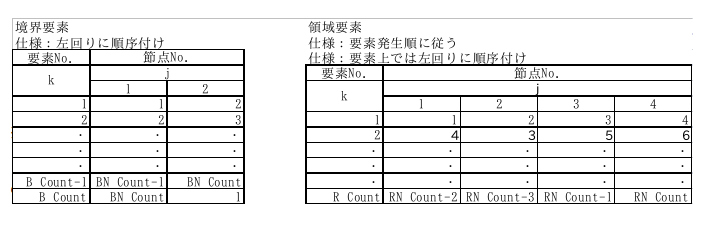
※ 領域要素の番号付けは、具体的な要素発生が不明なので例です。
ここでB_Countは境界要素数,BN_Countは境界節点数。R_Countは領域要素数,RN_Countは領域節点数。これらは[入力部]で具体的に要素データと節点データが与えられた時に、セットされるべきものです。表中のjの下の1,2と1,2,3,4は、境界要素では1:始端,2終端を表し、領域要素ではこの順番で左回りに節点を順序付ける事を意味します。
要素-節点対応表はもちろん配列で定義しますが、十進BASICでは可変長配列が使えないので、最初に配列寸法の上限を決めておく必要があります。ここでは、配列寸法上限:1000、としておきます。
境界要素に対する要素-節点対応表は、EN_B(k,2)の形にします。
kが境界要素番号,2の並びが先の1,2に対応します。EN_B(k,2)の内容は、(k,1),(k,2)で指定される境界要素kが持つ節点番号です。
同様に領域要素ではEN_R(k,4)の形にします。
kが領域要素番号,4の並びが先の1~4に対応し、(k,j),j=1~4で指定される領域要素kが持つ節点番号を格納します。
節点の具体的情報が必要です。節点データは当然、座標データで入力されます。これも配列で定義すべきです。境界節点座標はBN(j,2),領域節点座標はRN(j,2)とします。jが節点番号,2の並びがx座標,y座標です。
次に未知ベクトルψとqです。式(2)の計算方針では、ψとqを一つの未知ベクトルz=(ψ q)tとして扱います。それが連立方程式の組み方として、最も単純だったからです。
理想的には節点jにおいてψj,qjですが、(ψ q)tとまとめた時点でもうその扱いはできません。ψの成分数は明らかに境界節点数BN_Countと同じです。j→ψj→z(j)です。従ってj→qj→z(BN_Count+j)です。確かにこの規則があれば、各未知数のzの中での位置の特定は簡単です。しかしいずれ[2]を考慮するのでした。その時には、もっと複雑な対応付けに迫られます。節点-未知数対応表も用意しておきましょう。後で手を加えたとしても、基本の形だけは、ここで整えます。
節点-未知数対応表はBN_Z(j,2)とします。
jが節点番号で,(j,1)がψjに対応するz上の成分番号,(j,2)はqjに対応するz上の成分番号です。
式(1)の(D1 D2)と(d1 d2)tブロックは、境界条件が与えられる場所と、その値を示すものでした。これらの情報も[入力部]でセットされるべきものです。境界条件が与えられる場所の情報は、BN_BP(j,2)とします。
jは節点番号で、(j,1)にはψjが与えられる/与えられないで1または0をセットします。(j,2)にはqjが与えられる/与えられないで1または0をセットします。(D1 D2)ブロックで境界条件を与えるべき列番号は、節点番号jからBN_Z(j,1または2)の値でわかります。(D1 D2)の成分に与える値は1です。
境界条件の値の情報は、BN_BV(j,2)とします。BN_BP(j,2)と同様です。BN_BP(j,2)の指定に対応する形で、具体的な境界条件の値を格納します。(d1 d2)tブロックで境界条件の境界値を与えるべき行番号は、jに従って、zの中で(ψ q)tの後に順番に並べるだけです。
とりあえず最外殻のアウトライン決定作業としては、こんなものです。しかしここまででも、かなり沢山の事を決定し、わかった事もあります。だから[メモ欄]に決めた事を書いておくんですよ。平たく言えば、変数定義の説明です。また宣言部では必要とわかった変数(配列)を、この時点でちゃんと宣言します。後で勝手に変なものを作らせないためにです。[入力部]~[出力部]にも、わかった事を出来るだけ具体的に書いておきます。特に実行者が「要素」である事を明確にします。
※後で勝手に変なものを作るのは、じつは本人だったりするんですよね(^^;)。
3.プログラミング言語の選択
本当は、1.と2.を勘案しながら、システムを記述する言語を選択すべきなんですが、途中でちょろっと漏らしたように、まぁ~十進BASICで行けると思います。アマチュアにとって「無料」は大事です(^^)。
REM [メモ欄]
REM B_Count:境界要素数
REM EN_B(k,2):境界要素-節点対応表,k=1~B_Count
REM (k,1):要素kの始端の節点No.,(k,2):終端の節点No.
REM R_Count:領域要素数,Region Elements Countの略
REM EN_R(k,4):領域要素-節点対応表,k=1~R_Count
REM (k,j),j=1~4:jに従って要素kの要素節点No.を左回りに格納
REM BN_Count:境界節点数
REM BN(j,2):境界節点座標,j=1~BN_Count,(j,1):節点jのx座標,(j,2):y座標
REM RN_Count:領域節点数
REM RN(j,2):領域節点座標,j=1~RN_Count,(j,1):節点jのx座標,(j,2):y座標
REM BN_BP(j,2):節点の境界条件の有無,j=1~BN_Count
REM (j,1):節点jのψjが既知なら1、そうでないなら0
REM (j,2):節点jのqjが既知なら1、そうでないなら0
REM BN_BV(j,2):境界条件の値,j=1~BN_Count
REM (j,1):節点jのψjに与える値
REM (j,2):節点jのqjに与える値
REM z(i):未知ベクトル,i=1~2*BN_Count
REM BN_Z(j,2):節点-未知数対応表,j=1~BN_Count
REM (j,1):ψjのzの中の位置,(j,2):qjのzの中の位置
REM 節点j→ψj→z(j),節点j→qj→z(BN_Count+j)
REM [宣言部]
REM 配列寸法の上限は1000
REM B_Count:境界要素数
REM R_Count:領域要素数
Dim EN_B(1000,2) REM 境界要素-節点対応表,k=1~B_Count
Dim EN_R(1000,4) REM 領域要素-節点対応表,k=1~R_Count
REM BN_Count:境界節点数
REM RN_Count:領域節点数
Dim BN(1000,2) REM 境界節点座標,j=1~BN_Count
Dim RN(1000,2) REM 領域節点座標,j=1~RN_Count
Dim BN_BP(1000,2) REM 節点の境界条件の有無,j=1~BN_Count
Dim BN_BV(1000,2) REM 境界条件の値,j=1~BN_Count
Dim BN_Z(1000,2) REM 節点-未知数対応表,j=1~BN_Count
Dim z(1000) REM 未知ベクトル,i=1~2*BN_Count
REM [入力部]
REM境界要素数B_Countと領域要素数R_Countは、事前に与えられると仮定する。
REM 境界要素と領域要素データは、要素ごとに節点番号が与えられると仮定する。
REM 与えられる節点番号は、左回りに順序付けられたものが与えられると仮定する。
REM 境界要素を要素番号kで読み込むLoop
REM Loop内で要素ごとの節点番号を読み、境界要素-節点対応表EN_B(k,2)をセット
REM 領域要素を要素番号kで読み込むLoop
REM Loop内で要素ごとの節点番号を読み、領域要素-節点対応表EN_R(k,4)をセット
REM境界節点数BN_Countと領域節点数RN_Countは、事前に与えられると仮定する。
REM 境界節点を節点番号jで読み込むLoop
REM Loop内で境界節点座標を読み、BN(j,2)をセット
REM 領域節点を節点番号jで読み込むLoop
REM Loop内で領域節点座標を読み、RN(j,2)をセット
REM 境界条件の場所を節点番号jで読み込むLoop
REM Loop内で節点jの境界条件の有無を読み、BN_BP(j,2)をセット
REM 境界条件の値を節点番号jで読み込むLoop
REM Loop内で節点jの境界条件の値を読み、BN_BV(j,2)をセット
REM 節点番号jのLoopで、節点-未知数対応表BN_Z(j,2)をセット
REM (j,1):ψjのzの中の位置,(j,2):qjのzの中の位置
REM 対応は、節点j→ψj→z(j),節点j→qj→z(BN_Count+j)
REM [計算部]
REM 境界要素番号kで境界積分を行うLoop
REM 要素番号kからEN_B(k,2)に従い節点を特定し、要素ごとに境界積分を実行
REM 上記結果に基づき、係数マトリックスBとHを作成
REM 領域要素番号kで領域積分を行うLoop
REM 要素番号kからEN_R(k,4)に従い節点を特定し、要素ごとに領域積分を実行
REM 上記結果に基づき、既知ベクトルwを作成
REM 境界節点番号jで境界条件位置を指定するLoop
REM 節点番号jからBN_BP(j,2)とBN_Z(j,2) に従い、(D1 D2)ブロックを作成
REM 節点番号jに従いBN_BV(j,2)の値をwブロックの後に並べ、(d1 d2)ブロックを作成
REM 全体係数行列が出来たので、Gaussの掃き出し法にかけ、未知ベクトルzを求める
REM [出力部]
REM BN_Z(j,2) に従いz(j)から値を読み出し、出力
(執筆 ddt³さん)
第19回 ひずみテンソルと応力テンソルの関係 [ネコ騙し数学]
第19回 ひずみテンソルと応力テンソルの関係
§1 ひずみテンソルと応力テンソルの関係
弾性体が変形し、その相対的な変位がvであるとする。このとき、ひずみテンソルΦの成分は
となる。
等方的な弾性体では、応力テンソルΨとひずみテンソルΦの主軸は同じと考えられるので、ΦとΨの共通な主軸の方向の長さ1のベクトルをa、b、cとする。ひずみテンソルの主値と応力テンソルの主値をそれぞれε₁、ε₂、ε₃、σ₁、σ₂、σ₃としたとき、
という関係が成り立つものとする。
等方的なので、
と考えられので、(1)式を
と変形することができる。
ここで、
とすれば、(2)式は
また、
は不変量で、体積膨張率である。
したがって、
である。
同様に、
つまり、
である。
このλ、μをLamé(ラメ)の定数と呼ぶ。
また、応力テンソルΨは
これに(3)式を代入すると、
単位テンソルをIとすると、
また、
だから、
ひずみテンソルの成分を、応力テンソルの成分を
とすると
となる。
テンソル積と単位テンソルを行列で表すと、
だから、
また、
§2 弾性体の釣り合い
弾性体内の各点の密度ρに比例した力ρKが単位体積あたりに働いているとする。さらに、弾性体の変形にともなう応力テンソルをΨとする。
弾性体内の任意の領域をVとし、その表面をS、Sの外法線ベクトルをnとする。
このとき、力の釣り合いは
(テンソルの)ガウスの発散定理から
Vは任意に選べるので、
となる。
これが弾性体の釣り合いの方程式である。
Kの成分を、Ψの成分を
とすると、
特に、K=0のとき、
つまり、
である。
弾性体が等方的であるとき、
となるので、よって、(6)式は
となる。
材料力学のお話2 [ネコ騙し数学]
材料力学のお話2
このとき、直交座標系O-x₁x₂に関する応力テンソルTの成分は
となる。
直交座標系O-x₁x₂を原点Oを中心に反時計回りにθ回転させた直交座標をO-x'₁x'₂をとすると、x'₁軸、x'₂軸の方向余弦は
だから、
とおくと、座標系の変換によって応力テンソルの変換式は
となる。
したがって、
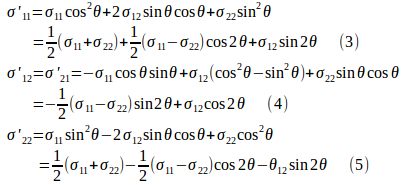
になる。
問1 直交座標系O-x₁x₂に関する応力テンソルが
であるとする。
原点を中心に座標軸を反時計回りにθ回転させたたとき、応力テンソルの成分はどのようになるか。
【解】
(解答終)
問2 直交座標系O-x₁x₂に関する応力テンソルが
であるとする。
原点を中心に座標軸を反時計回りに45°回転させたたとき、応力テンソルの成分はどのようになるか。
【解】
(解答終)
問2のように、単純せん断応力の場合、軸を45°回転すると、応力テンソルからせん断応力を消すことができる。
のとき、応力テンソルの成分は
したがって、となるように、
θをとれば、は応力テンソルの主応力(主値)になる。
また、主応力は、次のように、行列(テンソル)の固有方程式を解くことによて求めることができる。
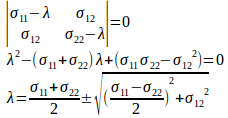
よって、主応力をσ₁、σ₂とすると、
となる。
せん断応力の絶対値が最大になるとき、その
を最大せん断応力(主せん断応力)といい、主応力σ₁、σ₂を用いると、
で与えられる。
問3 σ₁₁=2+√2、σ₂₂=2−√2、σ₁₂=√2のとき、主応力とその方向を求めよ。また、最大せん断応力を求めよ。
【解】
(6)より、
また、主応力は(7)より
よって、(8)より最大せん断応力は
である。
(解答終)
O-x₁x₂に対し角度θだけ傾いている(仮想的な)断面に作用する垂直応力σ'とせん断応力τ'は、この断面の垂直なベクトル、すなわち、法線ベクトル(直交座標系O-x'₁x'₂での成分であることに注意!!)
に、(3)〜(5)で与えられる成分をもつ応力テンソルを作用させることにより、次のように求めることができる。
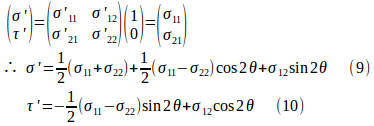
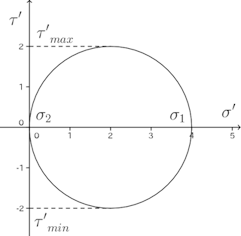
このθを消去すると、
これをモールの応力円という。
となり、これを用いて、主応力、最大せん断応力を求めることもできる。
材料力学のお話 [ネコ騙し数学]
材料力学のお話
ひずみと応力についての理解を深めるために、材料力学の話をすこしだけすることにする。
 右図のように長さl₀、断面積Aの棒を力Fで引っ張ったところ、長さがlになったとする。
右図のように長さl₀、断面積Aの棒を力Fで引っ張ったところ、長さがlになったとする。
このとき、
を垂直ひずみといい、
を引張応力という。
力の向きが図とは逆の場合は、圧縮。
この棒が弾性体の場合、応力が弾性範囲内にあるとき、「応力はひずみに比例する」というフックの法則が成り立つので、
という関係が成立し、この比例定数を縦弾性係数という。
 また、右図のように、面DC(紙面に垂直な方向の厚さを1とする)に力Fがかかり、ABCDがABC'D'に変形したとする。
また、右図のように、面DC(紙面に垂直な方向の厚さを1とする)に力Fがかかり、ABCDがABC'D'に変形したとする。
このとき、
をせん断歪ひずみという。
θ(単位はラディアン)が微小なとき、
と近似できるので、せん断ひずみγは
また、面DCの面積をAとするとき、
をせん断応力といい、弾性範囲内ならば
が成立する。この比例定数Gを横弾性係数(せん断弾性係数、ずれ弾性係数)という。
 さて、右図のように、上の棒の横断面BB'に対しθの角度をなす断面BCでの力の釣り合いを考える。
さて、右図のように、上の棒の横断面BB'に対しθの角度をなす断面BCでの力の釣り合いを考える。
BCに垂直な方向の力をN、CBに平衡な力をTとすると、
という関係がある。
また、断面BB'の断面積はAだから、断面BCの断面積A'は
しがたって、断面BCに垂直な応力をσ、BCに平行なな応力をτとすると、
ここで、
とおくと、
ということで、せん断応力τが最大になるθは、2θ=90°のときだから、
そして、一般に金属などの材料は、引張や圧縮には強いけれど、横方向の力(せん断力)には弱いものらしい。
したがって、上の棒のように引っ張っていても、斜め45°ちかくの方向にまず亀裂が発生し、そこから亀裂が走り、破壊するものらしい。
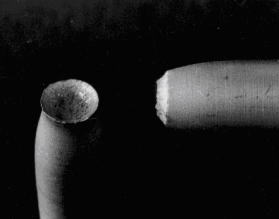
画像元:http://ms-laboratory.jp/strength/4_1/4_1.htm
それはそれとして、(8)、(9)式より、
sin²2θ+cos²2θ=1という関係があるから、
が成立する。