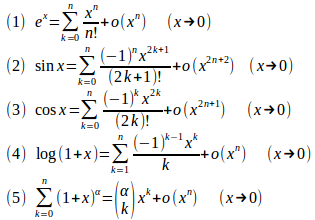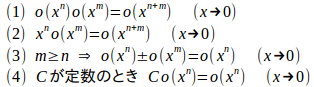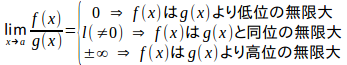微分法を用いた相加平均≧相乗平均の証明 [ネコ騙し数学]
微分法を用いた相加平均≧相乗平均の証明
問題 次の問に答えよ。
（１） 
であることを証明せよ。
（２） 
ならば
であることを証明せよ。
（３） 
ならば
であり、等号が成立するのは
のときに限ることを示せ。
［解］
（１） 
とおくと、
x<0でf'(x)<0、x>0でf'(x)>0だから、f(x)はx=0で極小（最小）である。
したがって、
（２） 
とおくと、
そして、（１）より
よって、
等号成立が成立するのは、
のとき、すなわち、
（３）
とおくと、
よって、（２）より
等号が成立するのは、、すなわち、のときである。
f(x)が
級のとき、 Taylorの定理から
となるcがxとaの間にある。
したがって、f''≧0のとき、つまり、凸関数のとき、
である。
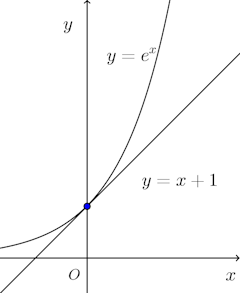
とおくと、これは点(a,f(a))における接線だから、f(x)のグラフは接線の上側にあることになる。
は凸関数で、問題の（１）の不等式の右辺はx=0における曲線の接線だから、直接的にではないけれど、相加平均≧相乗平均の証明で凸関数の性質を使っていると言えるのかもしれない。
ランダウの記号を用いた極限の計算法 [ネコ騙し数学]
ランダウの記号を用いた極限の計算法
まずは、ランダウの記号（スモール・オー）の定義を示す。
のとき
とあらわす。
そして、前回紹介した漸近展開の定理を再掲する。
定理 （漸近展開）
f(x)が0を含む開区間Iで
級関数であるとき
である。
指数関数
をマクローリン展開すると
となるから、
である。
したがって
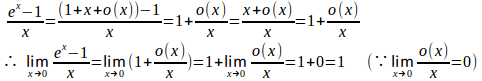
同様に、
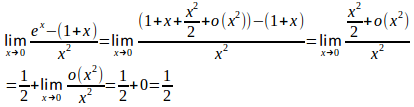
と、ランダウの記号を用いて極限の計算をすることができる。
問題１ ランダウの記号を用いて次の極限値を求めよ。
【解】
（１） マクローリン展開より
したがって
（２） マクローリン展開より
したがって
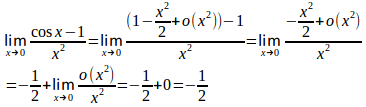
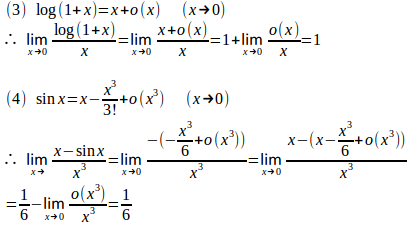
（解答終了）
問題２ マクローリンの定理を利用して、次の極限を求めよ。
【解答】
（１） マクローリンの定理より
したがって、
よって、
（２） マクローリンの定理より
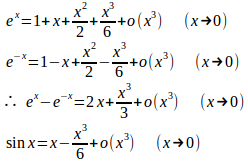
よって、
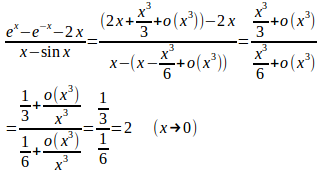
よって、
（解答終了）
第１５回 ランダウ記号の性質 [ネコ騙し数学]
第１５回 ランダウ記号の性質
ランダウ記号の定義をあらためて示す。
ランダウの記号の定義
関数f(x)、g(x)が
であるとき、
で表す。
定理 （漸近展開）
f(x)は、0を含む区間Iで
級とする。このとき、
である。
［証明］
マクローリン（テーラー）の定理より、関数fは、任意の点x∈Iで、
であるθが存在する。
よって、
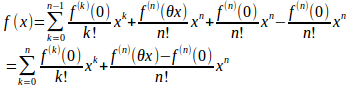
とおく。
x→0のときθx→0で、fは級だから
よって、
である。
したがって、
（証明終了）
上の定理から代表的な初等関数の漸近展開が次のように求められる。
ここで、
である。
ランダウの記号を用いて複雑な極限の計算をするときに必要になるので、ランダウの記号の演算規則を紹介する。
定理 （ランダウの記号の演算規則）
【略証】
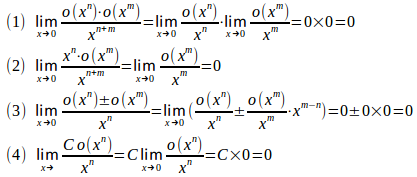
（証明終）
数値計算などでは、ビッグ・オーOを用いることが多いので、次の定理とその証明を紹介する。
その前に、ランダウ記号のビッグ・オーOの定義を示す。
定義（ランダウのビッグ・オーO）
関数f(x)、g(x)が
であるとき、
で表す。
定理 （漸近展開）
関数f(x)が原点の近傍｜x｜<r（r>0）で
級ならば
である。
［証明］
f(x)は原点の近傍｜x｜<rで級の関数だから
は｜x｜<rで連続。
したがって、0<r₀<rをとると、は｜x｜≦r₀で連続だから有界（＊）で、
となる実数Kが存在する。
f(x)を原点でマクローリン展開すると、
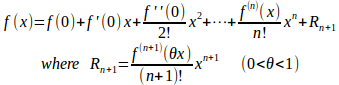
よって、｜x｜≦r₀（x≠0）のとき
である。
（証明終）
（＊）
有界閉区間Iで連続な関数f(x)は、Iで最大値M、最小値ｍをとる。
だから、
にとれば
したがって、有界閉区間で連続な関数は有界である。
問題とその答え [ネコ騙し数学]
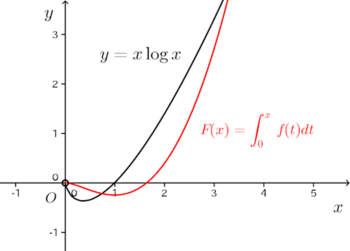
問題 次の関数f(x)について下の問に答えなさい。
（１） 次の極限を求めなさい。
極限を求める際にロピタルの定理を使ってよいものとする。
ロピタルの定理
関数f(x)、g(x)は開区間(a,b)で微分可能な関数とする。
、g'(x)≠0のとき、
が存在すれば、
も存在し、
である。
（２） この関数はx=0で右側微分可能でしょうか。つまり、次の右極限
が存在するでしょうか。存在するならば、その値は。
（３） 閉区間[0,a]（a>0）で積分可能ですか。
積分可能ならば、
を求めてください。
［解］
（１） ロピタルの定理より
（２）
だから、
したがって、x≠0のとき
だから、
は存在しない。
（３） f(x)は閉区間[0,a]（a>0）で連続。したがって、f(x)は[0,a]で積分可能。
x=0における（右側）微分係数は
したがって、x≧0で
が成立する。
よって、
（y=xlogxのグラフは❍（原点）を含まない。）
［解答終］
x>0のとき
無限大、無限小とランダウ記号 [ネコ騙し数学]
無限大、無限小とランダウ記号
§１ 関数の無限大、無限小
aを実数または±∞とする。
ならば、x→aのときf(x)は無限小であるという。
ならばx→aのときf(x)は無限大であるという。
関数f(x)、g(x)が点aで無限小のとき、
という。
例１
f(x)=x²,g(x)=xとすると、x→0のとき
だから、f(x)はg(x)より高位の無限小。
f(x)=sinx、g(x)=xとすると、
だから、f(x)とg(x)と同位の無限小。
f(x)=x、g(x)=x²とすると、
だから、f(x)はg(x)より低位の無限小。
関数f(x)、g(x)が点aで無限大のとき、
という。
例２
f(x)=logx、g(x)=xとすると、
だから、logxはxよりも低位の無限大。
、g(x)=xとすると、
だから、はxよりも高位の無限大。
問 次のことを示せ。
［解答（？）］
ロピタルの定理より
［解答（？）終了］
§２ ランダウの記号
x→aのとき、f(x)/g(x)が無限小、つまり、
のとき、
で表す。この記号o(g(x))をランダウ記号（oをランダウのスモール・オー）という。特に、
のとき
と定める。
例３ f(x)=sinxは、x→0ならばf(x)→0だから
また、f(x)=x²、g(x)=xとすると、x→0のとき、
だから、
しかし、f(x)=x、g(x)=x²のとき、
だから、
ではない。
つまり、
は、一般に成立しない。
x→aのときに、f(x)/g(x)が有界にとどまるならば、これを
で表す。（Oをランダウのビッグ・オーという）
特に、
のとき、
である。
例４
x→0のとき、
だから、
また、xが0に限りなく近いとき（ただし、x≠0）
だから、有界。
よって、
である。
ラウンダウ記号にはスモール・オーoとビッグ・オーOの２種類があるのだが、以降、スモール・オーo、つまり、o(g(x))をランダウ記号と呼ぶことにする。
漸近線 [ネコ騙し数学]
漸近線
曲線上の点が原点から限りなく遠ざかっていくとき、その点からの距離が限りなく0に近づく直線を漸近線という。
例
グラフから明らかなように、この曲線は、x→1+0のときy=+∞、y→1−0のときにy=−∞だから、この曲線上の点(x,f(x))は、xが１に近くづけば近づくほど原点からの距離が限りなく大きくなって、かつ、直線x=1に近づくので、x=1はこの曲線の漸近線である。
また、同様に、x→±∞のとき
だから、この曲線は直線y=xに限りなく近づいていくから、y=xも漸近線である。
曲線y=f(x)の漸近線がy軸に平行な漸近線y=aについては、
が成立するかどうかを調べればよい。
次に、曲線y=f(x)の漸近線がy軸に平行でなく、直線y=mx+nに近づく場合について考える。
曲線y=f(x)上の点P(x,y)から直線y=mx+nにおろした垂線の足をQとする。
このとき、線分PQの大きさは
x→±∞のとき、PQ→0だから
よって、
したがって、
である。
特に、m=0のとき、
より、
が漸近線となる。
問 次の漸近線を求めよ。
【解】
（１）
したがって、
よって、y=xは漸近線。
また、
だから、x=0も漸近線。
したがって、漸近線はy=x、x=0。
（２）
よって、y=x+3が漸近線。
x=0も漸近線。
したがって、漸近線はy=x、x=0である。
（解答終わり）
だが、上の問題は、必ずしもこのように解く必要はなく、
（１）であれば、
x→±∞のとき、1/x→0になるので、y=x+1/xがy=xに限りなく近づいてゆくことから、y=xが漸近線であることが分かる。
同様に、（２）の場合、
x→±∞のとき、カッコの中が限りなく0に近づくので、y=x+3が漸近線になることがすぐにわかる。
関数の凸凹に関する問題 [ネコ騙し数学]
関数の凸凹に関する問題
問題１ 関数f(x)は、開区間Iで２回微分可能、かつ、f''(x)>0とする。曲線y=f(x)は、Iで常に接線の上側にあることを証明せよ。
［解］
aを開区間Iの任意の点とすると、(a,f(a))における接線の方程式は
である。
平均値の定理より、
であるcがaとxの間に存在する。
よって、
Iでf''>0だからf'は単調増加。
したがって、x<aのとき、
x>aのとき
x=aのときF(a)=0。
よって、曲線y=f(x)は接線の上側にある。
（解答終了）
［別解」
f''(x)>0だから、f'(x)は（単調）増加関数。
よって、x<aのときf'(x)<f'(a)よりF'(x)<0で減少、x>aならばf'(x)>f'(a)でF'(x)>0で増加。
したがって、F(x)はx=aのときに極小で最小となり、
よって、曲線y=f(x)は接線の上側にある。
（別解終了）
微分積分の教科書や高校の参考書の中には、
「関数のグラフ上の点Pの近くで、そのグラフが点Pの上側にあるとき、グラフは点Pで下に凸、グラフが下側にあるとき、グラフは点Pで上に凸であるという」
といった関数の凹凸の定義を採用しているものもあるようです。
問題２ 関数fを区間Iで定義された二回微分可能な凸関数とする。f'(x)>0（x∈I）ならば逆関数f⁻¹は上に凸（凹）であり、f'(x)<0ならば下に凸であることを証明せよ。
［解］
x=f⁻¹(y)とすると、y=f(x)。
関数fが区間Iで下に凸のとき、f''(x)=y''≧0だから、関数fは、f'(x)=y'>0ならば
となり上に凸（凹）、f'(x)=y'<0ならば
となり下に凸である。
（解答終了）
問題３ f(x)=ax²+bx+c（a>0）について、次の不等式が成り立つことを証明せよ。
［解］
f'(x)=2ax+b、f''(x)=2a>0 （∵a>0） だから、f(x)は狭義凸関数。
A(x₁,f(x₁))、B(x₂,f(x₂))、C(x₃,f(x₃))とすると、f(x)は狭義凸関数なので、線分AB、BC、ACは曲線y=f(x)のグラフの上側にある。
とすると、これは△ABCの重心で、△ABCの内部にある（図を参照）。
したがって、
（解答終了）
何でも数式を使って証明すればいいというものではないだろう。このように図形を利用した解法もありではないか。
問題２では、f(x)=ax²+bx+c（a>0）と２次の項が正である二次関数ですが、これはf''(x)>0であれば、狭義凸関数ならば成り立つ不等式。
２次関数に限定せず、より一般的に解いたというわけ。
しかし、こうした図的な解答は数学的でないという批判が出るかもしれないので、別解を。
［別解］
f(x)は狭義凸関数。
よって、
したがって
（解答終了）
凸関数と凹関数 [ネコ騙し数学]
第１２回 凸関数と凹関数
区間Iで定義された関数f(x)が、Iの任意の点x₁、x₂（x₁<x₂）に対して、x₁<x<x₂ ならば
であるとき、f(x)を凸関数という。また、このとき、f(x)は下に凸という。
であるとき、f(x)を狭義の凸関数という。
また、 –f(x)が凸関数であるとき、f(x)を凹関数という。
x₁<x<x₂ とすると、（１）式は
と変形され、さらに、
とおくと
となる。
したがって、f(x)が凸関数のとき、曲線y=f(x)上の任意の２点(x₁,f(x₁)と（x₂,f(x₂)）を結ぶ線分は、曲線y=f(x)の下側にはくることがない。
また、f(x)が凸関数のとき、
が成立し、
直線AC勾配≦直線ABの勾配≦直線CBの勾配
である。
aを区間Iの内部の点とする。関数f(x)が点aの左近傍で狭義凸（狭義凹）、点aの右近傍で狭義凹（狭義凸）、つまり、点aの前後で凹凸が入れ替わるとき、曲線y=f(x)上の点(a,f(a))を曲線の変曲点という。
例 点(0,0)は曲線y=x³の変曲点である。
定理 （凸関数と２次導関数）
関数f(x)が区間Iで連続、区間Iの内部で２回微分可能とする。f(x)がIで凸関数である必要十分な条件は、Iの内部でf''(x)>0であることである。
［証明］
区間Iの内部の任意の点をa、b（a<b）、a<x<bとする。
十分）
f(x)はIの凸関数だから
f(x)は微分可能だから
f'(x)はIの内部で（広義）単調増加であり、よって、f''(x)≧0である。
必要）
Iの内部でf''(x)≧0とすると、f'(x)はIで（広義）単調増加。区間Iの任意の２点a,bをとり、a<x<bとすると、平均値の定理より
であるξとηが存在する。
ξ<ηだから、
よって、f(x)はIで凸関数である。
（証明終）
定理 関数f(x)が区間Iで連続、区間Iの内部で２回微分可能とする。Iの内部でf''(x)>0ならば、狭義凸関数である。
［証明］
Iの内部でf''(x)>0とすると、f'(x)はIで（狭義）単調増加。
区間Iの任意の２点a,bをとり、a<x<bとすると、平均値の定理より
であるξとηが存在する。
ξ<ηだから、
よって、f(x)はIで狭義凸関数である。
（証明終）
次の定理は変曲点の定義より明らかだろう。（本当に(^^ゞ）
定理 関数f(x)が区間Iで連続、Iの内部で２回微分可能とする。aがIの内部の点で点(a,f(a))が変曲点であるならば、f''(a)=0である。
注意 y=f(x)=x⁴のとき、f'(x)'=4x³、f''(x)=12x²だからf''(0)=0になるが、y=x⁴は凸関数。したがって、上の定理の逆、「f''(a)=0ならば(a,f(a))は変曲点である」は一般に成立しない。
関数の極大と極小 [ネコ騙し数学]
関数の極大と極小
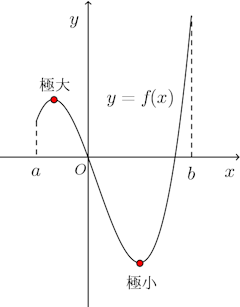点aを除くaの近傍の全てのxにおいてf(x)<f(a)であるとき、f(x)はx=aで極大であるといい、f(a)を極大値という。点aを除くaの近傍の全てのxにおいてf(x)>f(a)であるとき、f(x)はx=aで極小であるといい、f(a)を極小値という。極大値、極小値を合せて極値という。
定理 関数f(x)が点aで微分可能で、かつ、この点で極値をとれば、f'(a)=0である。
［証明］
f(x)が点aで極大であるとする。
f(x)が点aで極大だからf(x)<f(a)。
x<aのとき、
x>aのとき、
よって、f'(a)=0である。
f(a)が極小値のときも同様。
（証明終）
f(x)が開区間Iで微分可能、点a∈Iでf(x)が極値をとるとき、f'(a)=0である。
f(x)=x³（x∈R）とすると、f'(x)=3x²でf'(0)=0であるが、f(x)はx=0で極値を取らない。つまり、上の定理の逆、「f'(a)=0ならばx=aでf(x)は極値をとる」は、一般に成立しない。
定理 関数f(x)は点aの近傍で連続、aを除く点aの近傍で微分可能とする。x=aの前後で、f'(x)>0からf'(x)<0に変化するときf(x)はx=aで極大、f'(x)<0からf'(x)>0に変化するときx=aで極小である。
［証明］
x<aでf'(x)>0ならばf(x)は単調に増加し、x>aでf'(x)<0ならば単調に減少するから、x=aのとき極大でなる。
x<aでf'(x)<0ならばf(x)は単調に減少し、x>af'(x)>0ならば単調に増加するから、x=aのとき極小である。
（証明終）
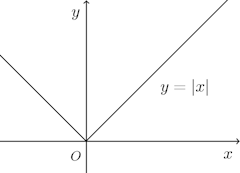f(x)=｜x｜はx=0で極小であるが、x=0で微分可能でないので、f'(0)は存在しない。しかし、
でx=0の前後でf'(x)の符号が−から＋に変じており、上の定理が成り立っていることがわかるだろう。
定理 f(x)が点aの近傍で微分可能で、かつ、f''(a)が存在するとき、
［証明］
だから、f'(x)はx=aで連続であり、xがaに十分近いとき、f''(a)と
は同符号である。
したがって、
f''(a)>0、x<aのとき
f''(a)>0、x>aのとき
よって、x=aの前後でf'(a)の符号が負から正に変わっていて、f(a)は極小値である。
f''(a)<0のときも同様。
（証明終）
f(x)が点aを含むある開区間Iで２回微分可能でf''(x)が連続であるとき、上の定理は
テーラーの定理（n=2）
となるcがaとxの間にすくなくとも１つある
を使うと次のように証明できる。
xをx∈Iかつx≠aである任意の点とする。
テーラーの定理とf'(a)=0より
となるcがaとxの間にある。
f''(x)はIで連続だから、点xと点aが十分近いとき、f''(c)とf''(a)は同符号。
したがって、f''(c)>0のとき、x≠aだから
よって、f(a)は極小値である。
同様に、f''(c)<0のときf(x)<f(a)となり、f(a)は極大値である。
先にあげたf(x)=x³の場合、f'(x)=2x²、f''(x)=6xだから、f'(0)=0、f''(0)=0だから、２次導関数の符号をを用いた極値の判定は出来ない。
f(x)=x³の時のx=0のようにf'(a)=0、f''(a)=0である場合、f(a)をx=aで３次でテーラー展開して判定すればよい。
となることから、
になる。
３次導関数f'''(x)が点aで連続でxとaが十分に近いとき、f'''(c)とf'''(a)は同符号。よって、f'''(a)>0のとき、x<aならばf(x)<f(a)、x>aならばf(x)>f(a)。したがって、f(x)はx=aで極値を取らない。f'''(a)<0のときも同様に、f(x)はx=aで極値を取らない。
このように２次より高次の導関数を用いて極値の判定を行うことが可能である。
テーラーの定理とテーラー展開、マクローリン展開 [ネコ騙し数学]
第１０回 テーラーの定理とテーラー展開、マクローリン展開
定理 テーラーの定理
関数f(x)は閉区間[a,b]でn−1回連続微分可能、開区間(a,b)でn回微分可能ならば
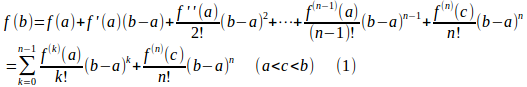
となるcが少なくとも１つ存在する。
［証明］
となるようにKを定め、
とおくと、F(a)=F(b)となる。
F(x)は[a,b]で連続、(a,b)で微分可能であり、F(a)=F(b)だからロールの定理よりF'(c)=0 となるcがa<c<bに少なくとも１つ存在する。
F(x)を微分すると、
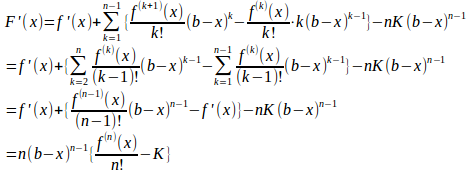
したがって、
（証明終了）
n=1とすると、平均値の定理が得られる。
極値の判定などで重要なn=2のときは以下のようになる。
b=x、
と置き、（１）式を書き直すと
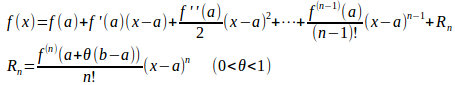
となり、
をLagrange（ラグランジュ）の剰余項という。
fが
級ならばすべての非負の正数nについて（１）は成り立ち、
である点xでは
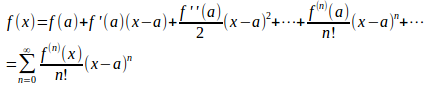
となり、この級数をx=aまわりのテーラー級数という。
特に、a=0のときに得られるx=0まわりのテーラー級数
をマクローリン級数という。
以下に代表的なマクローリン級数を示す。
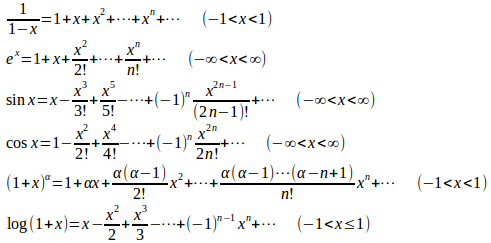
関数f(x)が
とべき関数の級数として展開されるとき、これはテーラー展開（マクローリン展開）に他ならない（テーラー展開の一意性）ことが知られている。
だから、
にx=–tを代入すると、
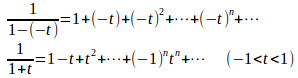
になるので、
のマクローリン級数を
と求めることができる。
同様に、
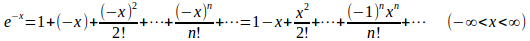
と、のマクローリン級数を利用して
のマクローリン級数を簡単に求めることができる。
