番外編 だ円の回転 [ネコ騙し数学]
番外編 だ円の回転
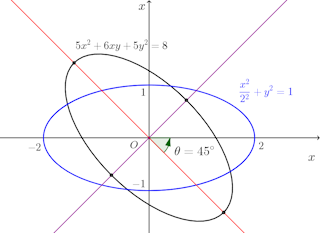
問題 曲線5x²+6xy+5y²=8
・・・①を原点のまわりにθだけ回転して、Ax²+By²=C・・・②の形にしたい。θの値をいくらにすればよいか。
点(x,y)を原点まわりで反時計回りにθだけ回転したときの点を(X,Y)とすると、(x,y)と(X,Y)との間には
行列で書くと、
何故ならば、cos90°=0だから。
 sin90°=1だから、④は
sin90°=1だから、④は
(解答終了)
回転させただけだから、だ円の面積は変わらない。
だ円、
したがって、
積分することなく、曲線①の面積が求まった。
ちなみに、赤い線がだ円①の長軸、紫色の線をだ円①の短軸という。
なぜ、そうなるかについては、将来、2×2の行列と1次変換について詳しく述べることにして、他の方法で回転角θを求めることもできる。
曲線①から
x+y=0は赤の直線、つまり、長軸の直線の方程式。
x−y=0は紫色の直線、つまり、短軸の直線の方程式。実はそれだけではなくて、
一般化すると、
包絡線 [ネコ騙し数学]
包絡線
αをパラメータとして含む曲線群
f(x,y,α)をC¹級とする。
曲線群と包絡線の接点を(x,y)とすると、xとyはαの関数である。これを
(1)と(2)は接するのだから、
ゆえに、包絡線は
逆に(4)の2つの方程式から
(4)より
(5)をαで微分すると、
(6)よりだから
したがって、でないならば接する。
少し補足説明する。
 例えば、
例えば、
αの値を一つに固定すると、たとえば、α=1とすると、①は中心(1,0)、半径1の円になる。
次にα=1/2とすると、中心(1/2,0)、半径1/2の円になる。このようにαを変化させれば、中心(α,0)、半径|α|の曲線群を得ることができる。
図から明らかなように、この曲線群は、αの値にかかわらず、y軸、つまり、x=0に接する。つまり、x=0が①の包絡線ということになる。
問題1 次の曲線群の包絡線を求めよ。

【解】
(1) αで偏微分すると

で、

よって、包絡線は放物線y²=4x
(2)
x=0は特異点の軌跡。
(解答終了)
したがって、x=0、y=αは特異点。
また、
問題2 次の包絡線を求めよ。
(1) 円x²+y²=r²のy軸に平行な弦を直径とする円の曲線群(2) 座標軸で切り取られる部分の長さが一定である曲線群
【解】 (1) 弦の両端をA、B、その中点をCとし、C(α,0)とする。
(1) 弦の両端をA、B、その中点をCとし、C(α,0)とする。
よって、円の方程式は
(2) 直線の方程式を

②をαで微分すると

③に代入すると、

とおくと、

よって、アステロイドになる。
(解答終了)台形公式の精度を求める問題 [ネコ騙し数学]
台形公式の精度を求める問題
台形公式の精度を求めるいい問題があったので紹介します。
問題
a<bのとき
この関数について、ロールの定理を繰り返して使うことによって
【解】
x=aのとき、
x=bのとき
よって、ロールの定理よりF'(c)=0となるa<c<bが存在する。
②を微分すると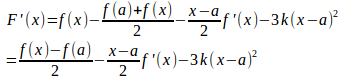
よって、F'(a)=0。
F'(a)=F'(c)=0かつ、F(x)は[a,c]で連続、(a,b)で微分可能。よって、ロールの定理より
ξ<>aだから、
(解答終了)
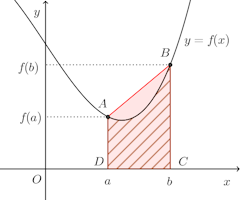
は、右図の台形ABCDの面積である。
問題の結果より、
[a,b]を
n等分したのだから、
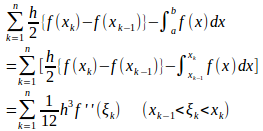
よって、
ここで、の最大値をMとすると、
ちなみに、以前紹介した中点公式
の誤差限界は
(1)と(2)のMは等しくないので単純な比較はできないけれど、Mが同一であれば、中点公式は台形公式の誤差の1/2ということになる。
だから、一般論になるけれど、中点公式の方が台形公式より精度はよいということになる。
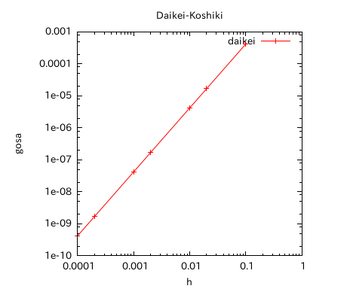
このグラフだと少しわかりにくいと思うのだが、h=0.1からh=0.01へとhが1/10になると、誤差は約その2乗である(1/10)²=1/100になる。
計算した生のデータのほうがわかりやすいと思うので、生データを以下に示す。
分割幅 h 誤差
0.010000 0.000004166667
0.001000 0.000000041667
0.000100 0.000000000417
この関数の場合、綺麗に1/100になっている。
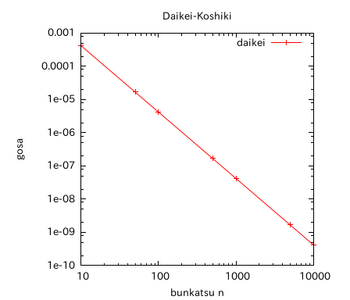 これだとまだ直観的に理解しづらいかもしれないので、[0,1]の分割数nと誤差との関係についてのグラフを示す。
これだとまだ直観的に理解しづらいかもしれないので、[0,1]の分割数nと誤差との関係についてのグラフを示す。
ワンポイントゼミ26 [ネコ騙し数学]
ワンポイントゼミ26
ねこ騙し数学の記事の中では
ちなみに、n!とは
ということで、
また、定義から
そして、さらに0!を
そうすると、
n=1のとき1!=2⁰
n=2のとき2!=2¹だから、①の不等式で等号が成立する。
n≧3では、⑨が成立する。この証明は、ねこ騙し数学の記事に書いてある。
ということで、
また
n=4のとき
n=kのとき
n=k+1のとき
![]()
では、ここで一つ問題!!
問題
n、mを1より大きい整数とする。このとき、
【答】
(n,m)=(2,4)、または、(n,m)=(4,2)2⁴=4²=16だからね〜。
しかし、これでは数学の解答にならない!!今日のねこ騙し数学の記事がヒントだにゃ。
②の両辺の対数をとる。
そうすると、
で、とりあえず、n≦mとする。
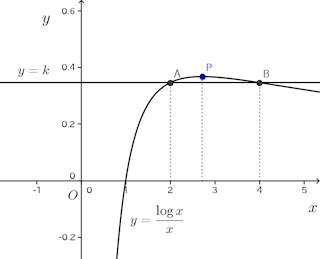
そうすれば、
そすると、この関数はx<eで増加、x>eで増加するから、上の方程式が解を2つもつためには、片方の解がx<e<3より小さくなる必要がある。
したがって、1<n<3を満たすnは2しかない!!
だから、n≦mのとき、2⁴=4²の組み合わせしかない。なのだが、
2⁴=4²または4²=2⁴を知らないヒト、あるいは、これに気づかないヒトはどうするんだろう。この問題は、大昔、とある私立大学の入試問題として実際に出題されたものだけれど、オレは試験会場でこの組み合わせに気づかないかもしれない(^^ゞ
この問題の解答には
「2⁴=4²は4²=2⁴」は既知として・・・と書いてあったように記憶している。
これは、難関(私立)大学を目指す受験生にとって既知の内容で、「2⁴=4²は4²=2⁴」は絶対に知っておかないといけないことだったのか。
解いてみるケロ [ネコ騙し数学]
解いてみるケロ
昔、東京大学の入試問題で「とπ³とどちらが大きいか」という証明問題が出されましたが、証明はできないものの、計算尺を使えばの
ほうが大きいとすぐ分かります。
http://www.pi-sliderule.net/sliderule/premise/toha.html
このようなことを書いてあるサイトがあったので、この大小関係を示してみることにするにゃ。
とπ³の対数を取ると、
になる。この2つの数を3π>0で割ると、
ちなみに、この対数は自然対数で、
さてさて、ここで次の関数を考える。
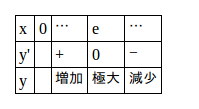
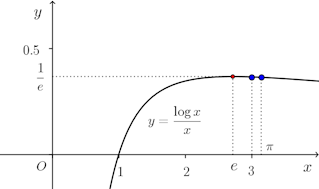 y'=0になるのはx=eのときだから、増減表を書くと、次のようなる。
y'=0になるのはx=eのときだから、増減表を書くと、次のようなる。e<3<πだから
これで大小が決まった。
ひょっとしたら、π>3であることを証明しないとマズいのかもしれない。
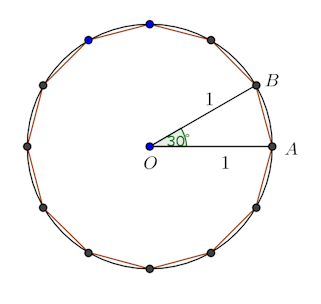 中心をOとする半径1の円を書くにゃ。右図のようにこの円に内接する正12角形を作る。そして、図のように正12角形の頂点A、Bと中心Oをそれぞれ結び、さらに、AとBを結ぶ。
中心をOとする半径1の円を書くにゃ。右図のようにこの円に内接する正12角形を作る。そして、図のように正12角形の頂点A、Bと中心Oをそれぞれ結び、さらに、AとBを結ぶ。そうすると、∠AOB=30°。
したがって、
eと3の大小関係は・・・
そこまで要求するか?
2項定理から
つまり、e≦3だケロ。
ということで、すべて、めでたく証明された!!
何だにゃ、
n=3のとき
n=k (k≧3) のとき成立すると仮定する。
つまり、
以上のことより、数学的帰納法によって⑨は成立する。
体積 座標軸以外の直線のまわりの回転 [ネコ騙し数学]
体積 座標軸以外の直線のまわりの回転
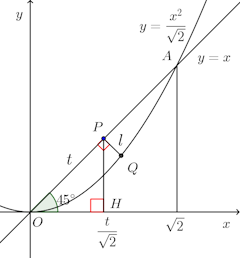
(1) 直線y=x上で原点からの距離がtである点をPとし、Pをとおりy=xに直交する平面でこの立体を切った切り口の面積S(t)を求めよ。
(2) この立体の体積を求めよ。【解】
(1) Pからx軸におろした垂線の足をH、Pを通りy=xに直交する直線と曲線y=x²/√2との交点をQとする。OP=tだから、Pの座標は
よって、点Qの座標は
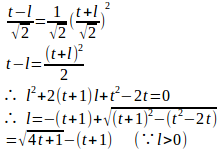
よって、切り口の面積S(t)は
(2) y=xとは原点Oと点A(√2,√2)で交わり、したがって、OA=2。
ここで、
で、とおくと、t=0にはu=1、t=2にはu=3が対応する。
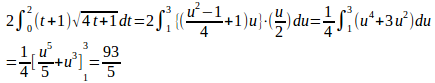
ゆえに、
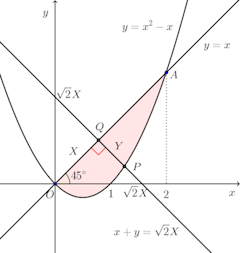
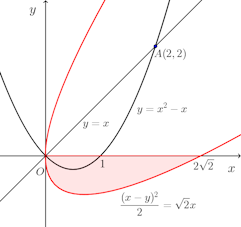 問題2 放物線y=x²−xと直線y=xとで囲まれた部分が、この直線のまわりに回転してできる立体の体積を求めよ。
問題2 放物線y=x²−xと直線y=xとで囲まれた部分が、この直線のまわりに回転してできる立体の体積を求めよ。
【解】
①をyについて解くと、
回転を利用すれば上の解答のように解くことができるが、次のように解くこともできる。
放物線y=x²−xと直線y=xの交点は原点OとA(2,2)。
曲線上の点P(x,y)からy=xにおろした交点をQ、
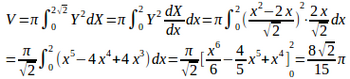
(解答終了)
あまりいい解き方ではないが、次のような解答を作ることもできるだろう。
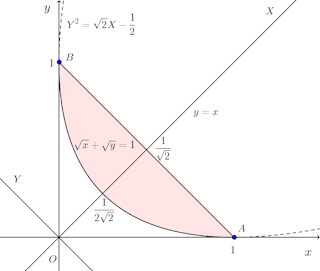
問題3 と座標軸とが囲む部分が点A(1,0)、B(0,1)を通る直線のまわりに一回転してできる立体の体積を求めよ。
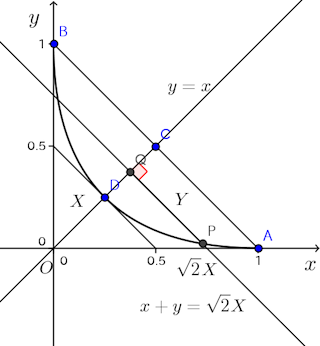 【解】
【解】は、媒介変数tを用いて
P(t³,1−2t+t²)からy=xにおろした垂線の足をQとし、
(解答終了)
これよりは、次のように解いたほうがいいだろう。
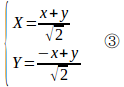
と変数を変換すると、②は
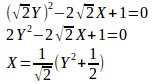
になる。
つまり、曲線①の正体は放物線の一部ということが分かる。
そして、このことを利用すると、次の問題を解くことができる。
【解】
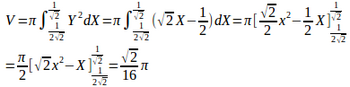
(解答終了)
関数方程式2 [ネコ騙し数学]
関数方程式2
問題1 微分可能な関数で、次の条件を満たすものを求めよ。
(1)
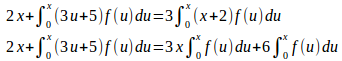
両辺をxで微分すると
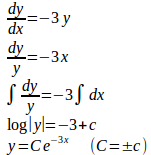
①にx=0を代入すると、
(2) x−t=uとおくと、t=x−uで、t=0にはu=x、t=xにはu=0が対応する。
また、dt=−duだから
よって、
よって、
問題2 [0,1]で定義された連続関数f(x)が連続な導関数f'(x)をもち、f(0)=2とする。
いま、この関数が、g(0)=g(1)=0をみたす[0,1]で連続な任意の関数g(x)(連続な関数g'(x)をもつとする)に対して
(1) f'(x)−3f(x)=0を証明せよ。
(2) f(x)を求めよ。【解】
(1) 部分積分すると
(2) y=f(x)とおくと
よって
4次精度のルンゲ=クッタ法で問題を解いてみた [ネコ騙し数学]
4次精度のルンゲ=クッタ法で問題を解いてみた
今日、11月24日に公開した数学の記事の第3問目は
この解は、問題3で求めたとおり
(1)の連立常微分方程式は
連立常微分方程式を解く(4次精度の)ルンゲ=クッタ法のアルゴリズムは次のようなもの。
ちなみに、上のアルゴリズムで使われている「=」は、数学の「等号」ではなく、右辺の計算結果を左辺に代入するという代入することをあらわしている。
4次精度のルンゲ=クッタ法はさすがに手計算でこれを行うのは大変なので、2次精度のルンゲ=クッタ法を使って、手計算で最初の値を求めてみることにする。
2次のルンゲ=クッタ法は次のようなアルゴリズム。
微分方程式(1)は
h=0.1とすると、
ちなみに、x=0.1のときの正しい値はy≒1.0050、z≒0.10017だから、こちらも精度よく計算できていることがわかる。
そして、x=0.2のとき、上の計算で得られたy=1.0025とz=0.1を使って同様の計算をする。次に、4次精度のルンゲ=クッタ法を用いて、h=0.1としたときの計算結果を示す。
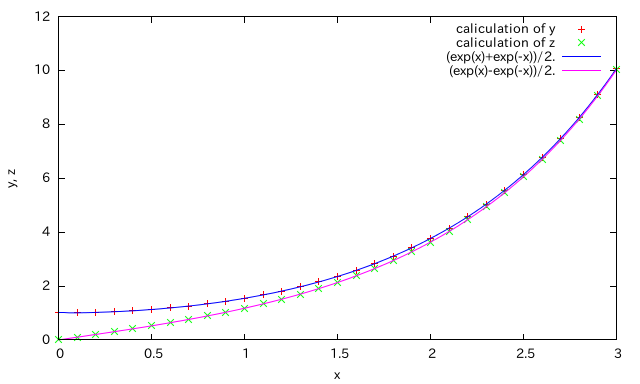
誤差は殆どなく、正確に計算できていることがわかると思う。
参考までに2次精度のルンゲ=クッタ法の計算結果を示す。
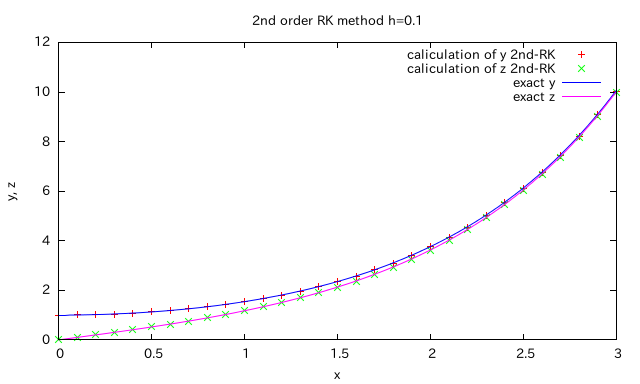
2次精度のルンゲ=クッタ法であってもこの程度の計算ならば、差は大きくない。
そこで、この両者の計算精度の差を明らかにするために、さらに複雑な次の連立常微分方程式を数値的に解くことにする
4次精度の計算結果は次の通り。
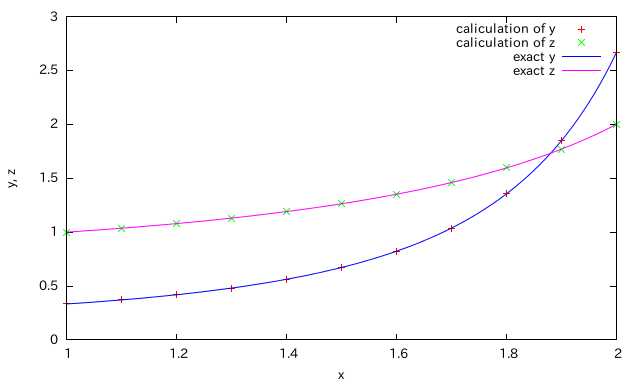
厳密解とよく一致している。
しかし、2次精度のルンゲ=クッタ法では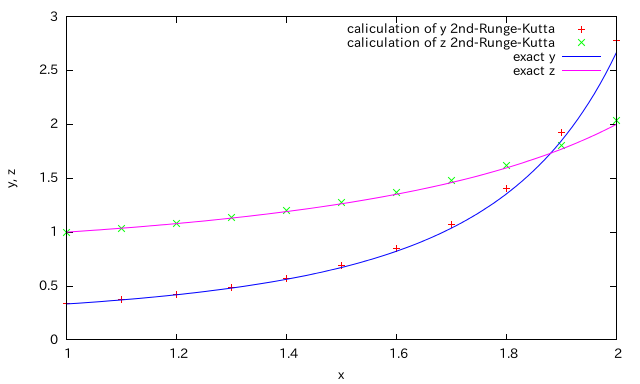
と、xが大きくなるにつれて、厳密解との差が次第に大きくなってゆく。
h=0.1からh=0.01とhを1/10にしたとしても、精度はやはりh=0.1のときの4次精度のルンゲ=クッタ法に及ばない。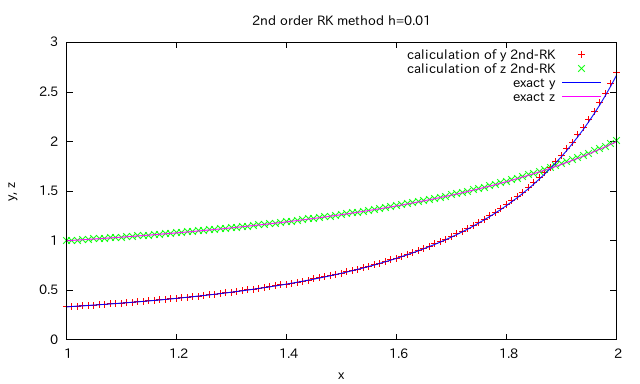
さらに1/10にしてh=0.001と、h=0.1の1/100したものが次のもの。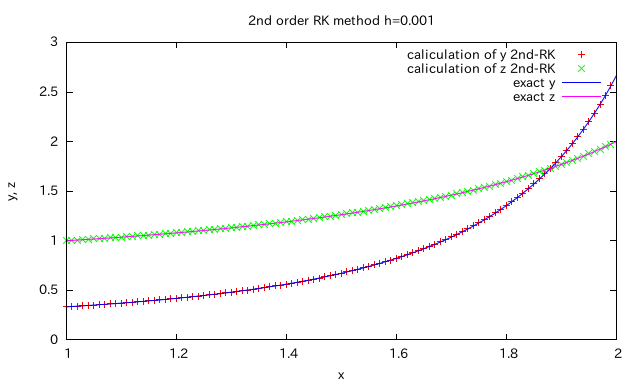
このとき初めて4次精度のルンゲ=クッタ法と2次精度のルンゲ=クッタ法は同程度の誤差になる。
4次精度のルンゲ=クッタのプログラムは以下の通り。
#include <stdio.h>
#include <math.h>
double f(double x, double y, double z) {
return x*y*z; // 変えていいのはここ
}
double g(double x, double y, double z) {
return x*y/z; //変えていいのはここ
}
// Runge_Kutta本体はいじらない方がいい
// いじらないでもいいように独立化させてある
// 独立化させているので、この部分は他のプログラムにそのまま流用可能!!
void Runge_Kutta(double x, double y, double z, double h ,double n) {
double dely1, dely2, dely3, dely4;
double delz1, delz2, delz3, delz4;
int i;
printf("%f %f %f\n",x,y,z); // 結果の出力(初期値)
for (i = 1; i <= n; i++) {
dely1 = h*f(x,y,z);
delz1 = h*g(x,y,z);
dely2 = h*f(x+h/2, y+dely1/2, z+delz1/2);
delz2 = h*g(x+h/2, y+dely1/2, z+delz1/2);
dely3 = h*f(x+h/2, y+dely2/2, z+delz2/2);
delz3 = h*g(x+h/2, y+dely2/2, z+delz2/2);
dely4 = h*f(x+h, y+dely3, z+delz3);
delz4 = h*g(x+h, y+dely3, z+delz3);
x=x+h;
y=y+(dely1+2*dely2+2*dely3+dely4)/6.;
z=z+(delz1+2*delz2+2*delz3+delz4)/6.;
printf("%f %f %f\n",x,y,z); // 結果の出力
}
}
main() {
int n;
double x, y, z;
double h;
h=0.1; // xの増分の設定 ココは変えてもよい
n=10; // 何回計算するかの設定 最終的にn×h進む
x=1; y=1./3.; z=1; // x,y,zの初期条件の設定
Runge_Kutta(x,y,z,h,n); // Runge-Kutta法を呼び出す
/* dy/dx=f(x,y,z), dz/dx=g(x,y,z)の初期値問題を
4次精度のルンゲ=クッタ法で解くプログラム */
// 注意 このプログラムで解く関数y,zはx=√7で不連続、ココでゼロ割発生!!
}
上のプログラムは、2つ目の微分方程式を解いている。
1つ目の微分方程式を解きたい場合、
double f(double x, double y, double z) {
return z; // 変えていいのはここ
}
double g(double x, double y, double z) {
return y; //変えていいのはここ
}
とし、mainの
x=1; y=1./3.; z=1; // x,y,zの初期条件の設定
を
x=0; y=1; z=0;
にすればよい。
関数方程式 [ネコ騙し数学]
関数方程式
問題1 a、bの任意の値に対してつねに、次の関係が成り立つように微分可能な関数f(x)を求めよ。
任意の定数aに対して
したがって、
問題2 すべての実数xに対して0でない関数f(x)があり、任意のx₁、x₂に対して
(1) f(0)=1であることを示せ。
(2) f'(0)=2であるとき、f'(x)の定義より、f'(x)=2f(x)であることを示せ。(3) 任意の実数xに対してf(x)>0であることを示せ。
(4) (2)で与えられた微分方程式からf(x)を求めよ。【解】
(1) x₁=x₂=0とすると
(2)
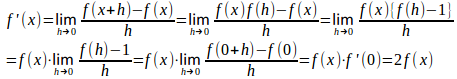
(3)
(4) y=f(x)とおくと、微分方程式f'(x)=2f(x)は
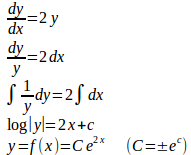
f(0)=1だから、C=1。
よって、
問題3 f(x)はすべての実数に対して定義され、正の値をとる連続関数で、
(1) F(x)=f(x)+g(x)、G(x)=f(x)−g(x)とするとき、
(2) f(x)を求めよ。
【解】(1)
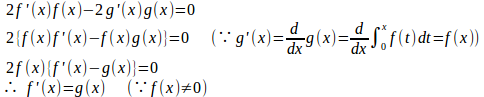
F(x)=f(x)+g(x)をxで微分すると
G(x)=f(x)−g(x)をxで微分すると、
(2) y=F(x)とおくと、
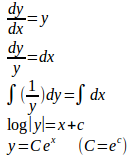
条件
よって、
問題では、f(x)だけを求めよとあるけれど、g(x)も簡単に求められるので、求めた。
実は、問題3で求めたf(x)、g(x)は双曲線関数と呼ばれるもので
たとえば、
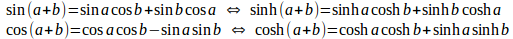
などなど。
そして、
陽解法による拡散方程式の解法の安定性 [ネコ騙し数学]
陽解法による拡散方程式の解法の安定性
次の拡散方程式がある。
陽解法は(1)を次の差分方程式に置き換えて、次の差分方程式を解くことによって(1)の近似解を求める。
とおくと、(2)は
つまり、
![]()
したがって、
のときに、は収束する。
上の議論は正確なものではないので注意。
このようにして、陽解法の
さてさて、この話は本当かということで、この検証のためのスプレッドシートを作り、実験してみた。
解く偏微分方程式は、
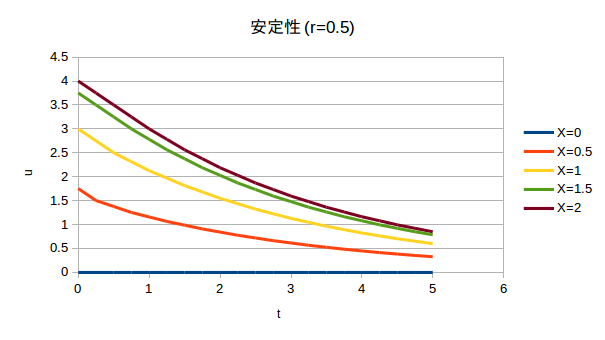
x=1とx=2の計算結果を示してある。
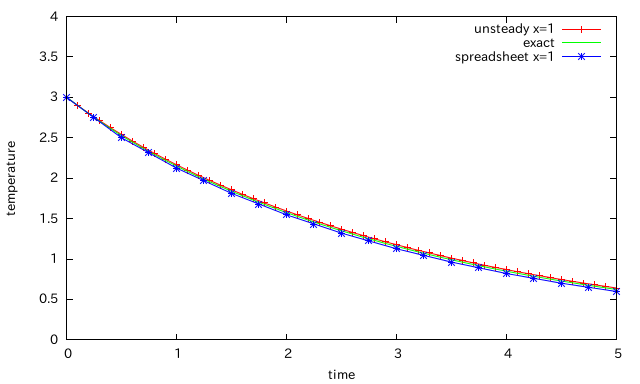
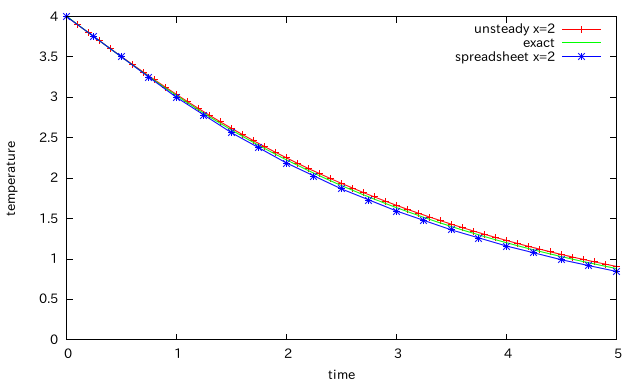
厳密解、そして、陰解法で解いた結果と良好な一致を見せており、このスプレッドシートの正当性を示している。
r=0.5の場合
r=0.6の場合。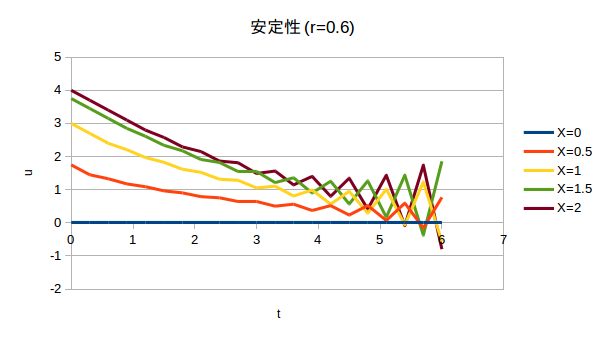
時間の経過とともに誤差が次々と伝播、増大し、数値解が激しく振動してしまう。