相似の演習編 ちょっとむずい問題 [ネコ騙し数学]
相似の演習編 ちょっとむずい問題
相似を使ったすこし難しい問題を解いてみることにします。
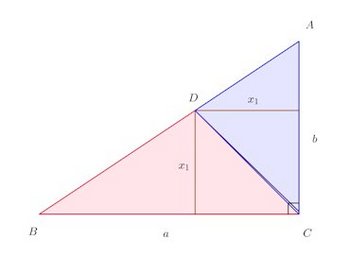
まずは、この問題から。問題1 図のように、直角三角形BC(BC=a、AC=b)内に、正方形S₁、S₂、S₃、・・・が並んでいるとき、
(1) S₁の1辺の長さをa、bであらわせ。(2) S₁、S₂、S₃、・・・の面積が等比数列をなすことを示せ。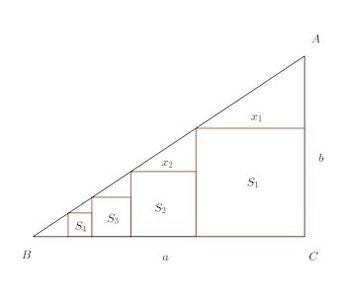
(1) △ABC∽△DBEだから
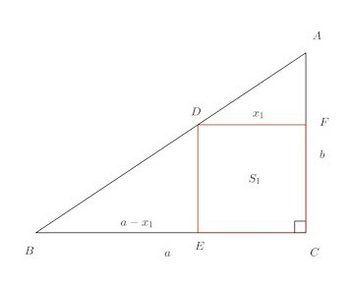
(2) △DBEと△ABCの相似比は
よって、は初項
(解答終わり)
大学入試の答案に書くのならば、もっと、きちんと書かないといけないのだろうけれど、ねこ騙し数学は大学受験を対象にしたものでないから、これでいいにゃ。
この問題にはないけれど、
なのですが、(1)についてうまい方法がある。
DとCを直線で結ぶ。そうすると、
補助線と三角形の面積を考えると、相似を使わなくても解ける・・・。
そして、
書いただけだにゃ。
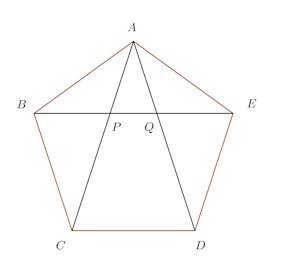
問題2 正5角形ABCDEの対角線BEがAC、ADと交わる点をP、Qとする。
(1) △ABE∽△PAB、△BAQ∽△APQを証明せよ。
(1) 正5角形の一つの内角は108°。また、一辺の長さは、それぞれ等しいので、
△ABE≡△BCA (2辺挟角)
よって、∠BAC=∠BCA=∠ABE=∠AEB=36°
したがって△ABE∽△PAB
また、∠BAQ=APQ=72°
∠ABQ=∠PAQ=36°よって、
△BAQ∽△APQ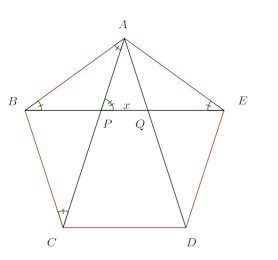
(2) PQ=xとおく。
AQ=AP=BP=BQ−PQ=AB−PQ=a−xまた、△BAQ∽△APQより
なのだけれど、
前回やったので、ネムネコたちは、正五角形の一辺と対角線の比が
そして、四角形BCDQは平行四辺形なので、BQ=CD=aだケロ。
このことを使うと、⑨から
こういうふうに解くことができるという話です。
ねこ騙し数学の記事を受験生が読んでいるとは思わないけれど、試験のとき、こんなふうに解いては駄目だケロよ。
番外編 ちょっと不思議な三角形の辺の長さを三角関数と相似を使って求める [ネコ騙し数学]
番外編 ちょっと不思議な三角形の辺の長さを三角関数と相似を使って求める
次の図に示すような頂角が36°、底角72°の二等辺三角形があるとする。
この時の、AB、BCの長さ1として、底辺の長さBCを、初等幾何の知識だけを使って求めてみることにするにゃ。
こんなの簡単だ。答えは
じゃ〜、sin16°の値はということになるんで(^^)
「⑨ネコ、疲れているんじゃないか。この値は、正弦関数の5倍角の公式を使えば、簡単に出てくるじゃないか。」
18×5=90だから、確かに、5倍角の公式(?)を使えば出てくる。
正弦関数の5倍角の公式はちょっと見当たらなかったけれど、余弦関数は
5θ=90°とすると、
実はウマイ方法がある。
よって、問題のxは
だけれど、これは相似を使うと、中学生でも求められるんだケロ。

∠Bの二等分線とACの交点をDとする。∠Bの二等分線なので、
∠DBA=∠CBD=72°/2=36°=∠Aになる。
だから、△ABDは二等辺三角形。また、
△ABD∽△ABCで、△ABDも二等辺三角形でBC=BD=xとなる。
△ABDも二等辺三角形なので、AD=BD=x。だから、CD=1−xとなる。
また、△ABD∽△BCDだから、
そして、この値は、黄金比
嘘じゃないケロ。
さらに言うと、この三角形は正五角形と深い関係があるのであった。
そして、この問題は、正五角形の対角線の長さを求めるのとほとんど同じ問題であったのであった。
第11回 相似3 [ネコ騙し数学]
問題1 △ABCの∠Aの外角の2等分線が辺BCの延長と交わる点をDとすれば

【解】
Cを通りADに平行な直線と辺ABの交点をFとする。
∠FCA=∠DAC (錯角)
∠CFA=∠EAD (同位角)
よって、△AFCは二等辺三角形。AF=AC
また、
なので、前回の問題と合せて、次の定理が成立する。
定理 △ABCにおいて、∠A(またはその外角)の2等分線が対辺(または、その延長線)と交わる点をDとすると、
AD:AC=BD:CD
である。問題2 である台形ABCDがある。ABをm:nに内分した点をMとし、MからADに平行線を引きDCとの交点をNとするとき、次の等式を証明せよ。


(1)
(2) 対角線ACとMNの交点をLとする。
△ABCと△AMLの相似比はm+n:mなので
まさかと思うけれど、なぜ、△ABC∽△AMLになるのかはわかるよね?
MLとBCが平行なので、∠AML=∠ABC (同位角)
∠MLA=∠BCA (同位角)∴ △ABC∽△AML
問題3
【解】
ABとCDが平行なので
∠PAB=∠PCD∠PBA=∠PDC
∴ △PAB∽△PCD△PAB∽△PCDだから

(証明終わり)
上の証明では、△PAB∽△PCDを証明しているけれど、
問題3のcは
で、さらにAとDを直線で結び、QPの延長線とADの交点をOとする。
となり、これは何かというとaとbの調和平均と呼ばれるものだにゃ。
これまでに、相加平均、相乗平均が出てきたにゃ。
a>0、b>0のとき
相加平均≧相乗平均
新たに出てきた調和平均と相加平均、相乗平均の大小関係ですが、相乗平均/調和平均は
なので、相乗平均≧調和平均となり、
a>0、b>0のとき
第10回 平行線と線分の比 [ネコ騙し数学]
第10回 平行線と線分の比
§1 相似な三角形と線分の比
定理
三角形ABCにおいて、辺BCに平行な直線、AB、ACまたはそれらの延長と交わる点をD、Eとすると、

定理
または
ならば
である。

DEとBCが平行なので、∠ADE=∠B、∠DEA=∠Cとなり、△ABC∽△ADE。
よって、
したがって、
逆については、∠Aを共通(または対頂角)にしていて、この角を挟む線分の比が等しいので、△ABC∽△ADEとなり、このことから、∠ADE=∠B、∠DEA=∠C、つまり、同位角が等しいので、DEとBCは平行である。
あるいは、Dを通り、ACに平行な直線とBCの交点をFとする。そうすると、△ADE∽△DBFになるので、
補助線一本で解決する。このあたりが初等幾何の醍醐味だにゃ。
問題1
下の図でAC、BD、EFはそれぞれ平行である。x、y、zの値を求めよ。
【答】
x=2,y=4.5, z=1.4
問題2
下の図で

QPの値を求めよ。
【解】有名問題のようで、高校入試によく出るらしい。
△APB∽△PDC
この問題については、次回でもう一度取り上げ、詳しい話をするにゃ。
DAとCEは平行なので、
∠CAD=∠ACE (錯角)
∠CAB=∠CEA (同位角)よって、△ACEは二等辺三角形で、
AC=AEしたがって、
【別解】
θ=∠BAC/2とする。
よって、
§2
平行線と比例

定理 ならば
証明は補助線一本。

番外編 微分積分 難しい問題(?)を解くネムネコ(暫定版) [ネコ騙し数学]
番外編 微分積分 難しい問題(?)を解くネムネコ(暫定版)
問題 区間0≦x≦1における関数
(1) f(x)=0は、0<x<1において、ただ一つの解を持つことを証明せよ。
(2) 上の解をαとするとき、(3) 与えられた区間における曲線y=f(x)と、x軸およびy軸とで囲まれた部分の面積をとするとき、
を求めよ。
(1)
また、
よって、f(x)=0は0<x<1において、ただ一つの解を持つ。
(2)
(3)
(解答終わり)
とか、解けばいいんじゃないか。
ちったぁ〜、ネムネコのことを見直したケロか?
番外編 相似と無限級数の応用問題 [ネコ騙し数学]
番外編 相似と無限級数の応用問題
いきなり、問題!!
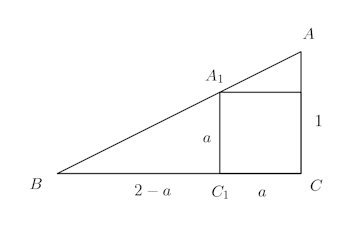
問題 図のように、∠C=90°、BC=2、CA=1の直角三角形に内接する正方形の辺の長さaを求めよ。
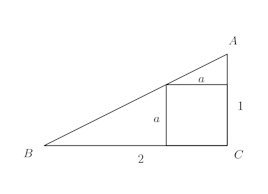
【解】
△ABC∽△A₁BC₁
よって、
このことから、△ABCと△A₁BC₁の相似比が3:2であることがわかるにゃ。
これでオシマイじゃ〜ない。本題は、これからだにゃ。
本題 図のように、∠C=90°、BC=2、CA=1の直角三角形内に正方形S₁、S₂、S₃、・・・が際限なく並んでいる。
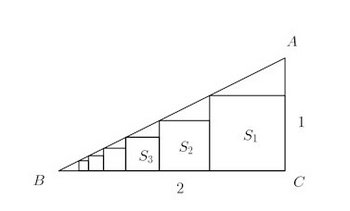
このとき、
【解】
問題から正方形S₁と正方形S₂の相似比が2/3であることがわかる。だから、相似な図形の面積比は相似比の2乗だから
同様に、
よって、
初項a、公比rの数列の一般項は
第9回 相似 [ネコ騙し数学]
第9回 相似
§1 相似
一つの図形を形を変えずに一定の割合で拡大、縮小した時に、その図形はもとの図形と相似であるという。
相似な図形では、(1) 対応する辺の長さの比は全て等しい
(2) 対応する角の大きさはそれぞれ等しい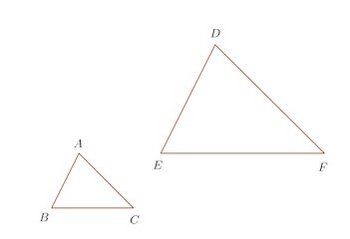
図に示してある△ABCと△DEFは、
∠A=∠D、∠B=∠E、∠C=∠F
だから△ABCと△DEFは相似であり、△ABC∽△DEFであらわす。§2 相似の中心
相似な図形の対応する点どうしを結ぶ直線がすべて1点Oで交わり、その点から対応する点までの距離の比がすべて等しいとき、その点Oを相似の中心とよび、それらの図形は相似の位置にあるという。
相似の位置にある図形は相似である。

§3 三角形の相似条件
定理 2つの三角形は、次の条件のどれか一つが成り立てば相似である。
1 3組の比がすべて等しい2 2組の辺の比とその辺の間の比が等しい
3 2組の角の比が等しい
で、
そうすると、三角形の合同条件から
△AB'C'≡△DEFよって、
△ABC∽△DEFちなみに、k>1のとき拡大であり、k<1のとき縮小。
こういった話でございます。
§4 問題
問題1 下図において、∠ACD=∠B、AC=8、CD=9、BC=12である。

(1) △ACDと△ABCは相似である。その相似比を求めよ。
(2) 線分ADの長さを求めよ。
(3) 線分ABの長さを求めよ。【解】
(1) ∠Aは共通。そして、∠ACD=∠Bなので、△ACD∽△ABC
相似比は
(2) 分数のほうが好きなので・・・
(3)
問題2 次の図で、∠A=∠R、AD⊥BC、BEは∠Bの二等分線である。△ABEと△ABFと相似な三角形を見つけよ。
【答え】
問題3 ACの長さを求めよ。

【解】
△ABCと△DBAに注目。∠Bは共通。
△ABC∽△DBA
相似比は3:2なので
第8回 問題演習 [ネコ騙し数学]
第8回 問題演習
問題1 次の図のxをa、b、cを用いてあらわせ。

【解】
外角定理より
問題2 線分AB上に点Cをとり、正三角形ACD、CDEをかき、AとE、BとDを結ぶ。
△ACE≡△DCBであることを証明せよ。AC=DC
CE=CB
∠ACE=∠DCB (∵ ∠ACE=∠ACD+∠DCE=∠DCE+∠CBE=∠DCB)よって、
△ACE≡△DCBちなみに、△ACDと△CDEは正三角形なので、∠ACD=∠CBE=60°
問題3
平行四辺形辺BCの延長上の点をEとし、∠DCEと∠CDEの二等分線が辺ADまたはその延長上で交わるてんをそれぞれF、Gとする。DF=DGであることを証明せよ。仮定より、
∠BCF=∠FCD
また、BCとADは平行なので∠DFC=∠BCF=∠FCD
よって、△DFCは二等辺三角形でDF=DC ①
同様に、∠DCG=∠CGD
よって、DC=DG ②
①、②よりDF=DG
問題4
AB=ACである二等辺三角形ABCで、AC上に点をとると、AD=DB=BCであった。(1) BDは∠Bの二等分線であることを証明せよ。
(2) ∠Aの大きさを求めよ。(1) a=∠Aとする。
AD=DBなので△DBAは二等辺三角形で、
∠DBA=∠A=a外角定理より
∠CDB=2aまた、DB=DCなので
∠C=∠CDB=2aさらに、AB=ACなので
∠B=∠C=2aよって、BDは∠Bの二等分線である。
(2) ∠A+∠B+∠C=a+2a+2a=5a=180°
よって、∠A=a=36°
問題5
平行四辺形ABCDの∠Dの二等分線と辺AB、BCまたはその延長との交点E、Fとする。(2) AE=BCであることを示せ。
【解】
(1) AEとDCは平行であり、錯角は等しいから
∠ABC=∠D=60°
(2) ∠E=∠ADE
よってAE=AD=BC
問題はここまでなのですが、これで終ったら、ちょっとつまらないな。
(3) AD=9、FC=6のとき、ABの長さを求めよ。
答えは6だにゃ。
第7回 中点連結定理の続きと共線 [ネコ騙し数学]
第7回 中点連結定理の続きと共線
ネムネコの持っている高校生向けの受験参考書に次のような定理が出ている。
定理A
の台形ABCDにおいて、辺AB、CDの中点をM、Nとすると、
定理B
の台形ABCDにおいて、辺ABの中点をとおり、底辺BCに平行な直線は、対辺の中点Nを通る。

前回やった中点連結定理、中点連結定理2の台形バージョンというべき定理。
証明自体は、ACに対角線一本を引けば、簡単に(?)証明できる。
△ABCに注目すると、中点連結定理より、
△ACDに注目すると、中点連結定理より
①、③から下線を引いた、M、L、Nが同一線上に存在するということがポイントなんだケロ。
ひょっとしたら、こうかもしれないから。
今、求めたものは青い線で示されるMLとLNで、台形のAB、CDの中点MNを結んだ直線と違うかもしれない。
そして、このことは①と③から保証される。
共線
③つ以上の点が同一線上にあるとき、これらの点は共線であるといい、これらの点を共線点という。M、L、Nが共線点であることを証明しないといけない。
この場合は、平行線の公理によって共線であるとこと、共線点であることが保証される。直線外の1点をとおり、直線に平行な直線はただ1つである
何故ならば、
線分ML、線分LNは、点Lを通、BC(AD)に平行な直線上にあるから。もし、MLとLNが同一直線上になければ、MLを延長した直線と、LNを延長した直線はLを通るBCに平行な直線となり、Lを通りBCに平行な直線が2本あることになり、平行線の公理に反してしまう。だから、共線である。
ほとんど明らかだけれど、うるさいことを言うと、共線であることを証明しないといけない、もしくは、明言しないといけない。
中学、高校の初等幾何の教科書を持っていないので、ハッキリしたことは言えないのだけれど、このあたりは視覚に頼っているようで、結構、いい加減なようだ。
そして、次のような問題が出ると、パニクる(^^ゞ
問題
台形ABCDの平行でない2辺、AB、CDの中点をそれぞれP、Q、AB、CDの中点をそれぞれ、R、Sとするとき、次の問題に答えよ。
(1) P、S、R、Qは同一線上にあることを示せ。
(2) 次のことを証明せよ。
(1) △ABCに注目。中点連結定理より、
(2) 記号AD〜BCを説明すると、これは
AD〜BC=|AD−BC|のことで、AD>BCのときは
AD〜BC=AD−BCで、AD≦BCのとき
AD〜BC=BC−ADになる。
この問題の場合、ABとDCは平行でないのでAB≠DCとなり、AD>BCとAD<BCで場合分けしないといけないのだけれど、図のようにBC>ADの場合だけを証明するにゃ。△ABCに注目。中点連結定理より
まっ、そういうことで。
第6回 中点連結定理 [ネコ騙し数学]
第6回 中点連結定理
定理9 中点連結定理
△ABCにおいて辺AB、ACの中点をそれぞれM、Nとすれば
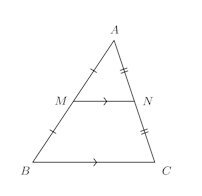
【証明】
証明は、次の図のようにMNを2倍に延長し、その端点をLとし、MとC、AとLを直線で結ぶ。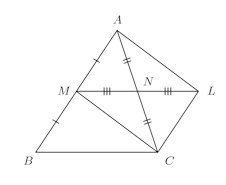
MN=NM
AN=NCよって、四角形AMCLの対角線を互いに2等分しており、四角形AMCLは平行四辺形。
四角形AMCLは平行四辺形だから、LCとAMは平行でかつAM=LC。
LCはAMに平行だから、MNにも平行。また、仮定より
MB=AM=LCよって、四角形MBCLは平行四辺形。
したがって、
(逆の証明)
∠AMN=∠LCM
∠NAM=∠NLCまた、
MN=LNよって
△NAM≡△NCLしたがって
AM=CL=MBAN=NC
ということで、
(証明終わり)
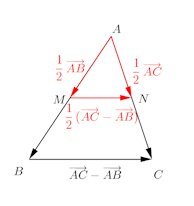
ベクトルによる証明は、循環論法の疑いがあり、証明になるかどうか怪しいけれど、
定理10 中線連結定理2
△ABCにおいて辺ABの中点MからBCに平行線をひけば、辺ACの中点を通る。
【証明】
辺ABの中点Mを通るBCに平行な直線とACの交点をNとする。
NをとおるABに平行な直線を引き、BCとの交点をLとする。
四角形MBLNは平行四辺形で、対辺の長さは等しいから、NL=MB=AM
ABとNL、ACとMNは平行なので∠NLC=∠B=∠AMN (同位角)
BCとMNは平行なので∠LCN=∠MNA (同位角)
よって、△AMN≡△NLC (1辺と両端の角相等)
よって、AN=NC
NはACの中点である。(証明終わり)
例題
4角形の対角線の中点を結ぶ線分と対辺の中点を結ぶ線分とは互いに他を2等分することを証明せよ。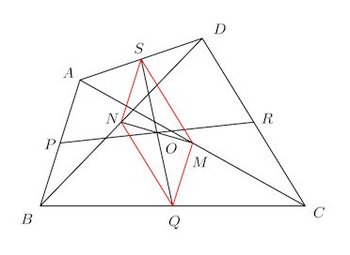
【証明】
4角形をABCDとし、図のように辺AB、BC、CDの中点をP、Q、R、Sとする。また、対角線AC、BDの中点をそれぞれM、Nとする。SがADの中点、NがBDの中点であるから、
ゆえに対角線SQとMNとは互いに他を2等分する。
同様に、4角形PMRNは平行四辺形だから、PRとMNも互いを2等分する。問題 平行四辺形ABCDの辺AD、BCの中点をそれぞれE、Fとすれば、BE、DFはACを3等分することを証明せよ。
【証明】
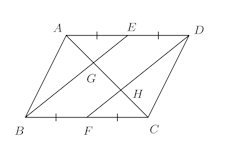
平行四辺形なので、
したがって、
EはADの中点なので、中点連結定理2よりGはAHの中点。
よって、AG=GH
△BCGに注目。同様に、HはGCの中点で、
GH=HCよって、
AG=GH=HCしたがって、BE、DFはACを3等分する。
(証明終わり)