ニュートン法による非線形連立方程式の近似解法2 [ネコ騙し数学]
ニュートン法による非線形連立方程式の近似解法2
ニュートン法を用いると、非線形方程式
の近似解(の一つ)を
と求めることができる。
前回、紹介したプログラムでは、偏導関数を与えて、
における偏微分係数
の計算をした。
この方法では、非線形方程式(1)の関数が変わるたびに、プログラムの利用者は、偏導関数を設定しなおさなければならず、何かと面倒。
――偏導関数の計算を間違う場合だってある(^^ゞ――
ニュートン法は、近似解法であること、そして、我々が欲しいのは、偏微分係数の正確な値ではなく、を修正するために必要な
であるのだから、偏微分係数
の値は近似値で十分なはずである。
したがって、十分小さなhを選び、中心差分をもちいて
と計算することにする。
h=1/10⁶程度にとれば、(6)式で計算した打切誤差は、せいぜい、1/10¹⁰程度で、その差はほとんど無視できる。
丸め誤差の範囲の程度だにゃ。
この方針に従ってあらたにプログラムを作ることにする。
! ニュートン・ラプソン法で非線形連立方程式f(x,y,z)=0,g(x,y,z)=0,h(x,y,z)=0を解く
! 偏微分係数を中心差分で代用
parameter (n=3)
real a(n,n+1)
limit = 20 ! 繰り返し計算の上限
del=1.e-6
eps=1.e-6 ! 収束判定に使用する何か
a=0. ! 行列の初期化
write(*,*) 'input x0,y0,z0'
read(*,*) x,y,z ! 計算開始時の初期値設定
write(*,*)
do iter=1,limit
! 偏微分係数の計算
fx=(f(x+del,y,z)-f(x-del,y,z))/(2.*del)
fy=(f(x,y+del,z)-f(x,y-del,z))/(2.*del)
fz=(f(x,y,z+del)-f(x,y,z-del))/(2.*del)
gx=(g(x+del,y,z)-g(x-del,y,z))/(2.*del)
gy=(g(x,y+del,z)-g(x,y-del,z))/(2.*del)
gz=(g(x,y,z+del)-g(x,y,z-del))/(2.*del)
hx=(h(x+del,y,z)-h(x-del,y,z))/(2.*del)
hy=(h(x,y+del,z)-h(x,y-del,z))/(2.*del)
hz=(h(x,y,z+del)-h(x,y,z-del))/(2.*del)
! 連立方程式の係数の設定
a(1,1)=fx; a(1,2)=fy; a(1,3)=fz; a(1,4)=-f(x,y,z)
a(2,1)=gx; a(2,2)=gy; a(2,3)=gz; a(2,4)=-g(x,y,z)
a(3,1)=hx; a(3,2)=hy; a(3,3)=hz; a(3,4)=-h(x,y,z)
call gauss(a,n,iflag) ! ガウス消去法で連立方程式を解く
if (iflag.eq.0) then ! エラー判定
write(*,*) 'エラー!! 連立方程式を解けない'
stop
end if
dx=a(1,4); dy=a(2,4) ; dz=a(3,4) ! 修正量 Δx,Δyをセット
x=x+dx; y=y+dy; z=z+dz ! 修正
err=amax1(abs(dx),abs(dy),abs(dz))
write(*,100) 'iter=',iter, 'x=',x,'y=',y,'z=',z
if (err.lt.eps) exit ! 収束したかの判定
end do
write(*,*)
if (iter.le.limit) then
write(*,*) '***solution***'
write(*,*) 'x=',x,'y=',y, 'z=',z
else
write(*,*) '収束しない'
end if
write(*,*)
write(*,*) 'check'
write(*,*) 'f(x,y,z)=',f(x,y,z),'g(x,y,z)=',g(x,y,z),'h(x,y,z)=',h(x,y,z)
100 format(a,i3,2x,2(a,f10.6,2x),a,f10.6)
end
! 利用者は連立方程式に合せてここの部分だけを変更
function f(x,y,z) ! f(x,y,z)=0の関数定義
f=x**3-2*y-2 ! f(x,y,z)=x³-2y-2=0
end
function g(x,y,z) ! g(x,y,z)=0の関数定義
g=x**3-5*z**2-7 ! g(x,y,z)=x³-5z²-7=0
end
function h(x,y,z) ! h(x,y,z)=0 の関数定義
h=y*z**2-1 ! h(x,y,z)=yx²-1=0
end
! 変更してよいのはここまで
subroutine Gauss(a,n,iflag) ! ガウス消去法
real a(n,n+1)
eps = 1.e-10
iflag = 1
! 前進消去
do k=1, n-1
! ピボット選択
i_max = k
do i=k+1, n
if (abs(a(i,k)).gt.abs(a(i_max,k))) i_max=i
end do
if (i_max.ne.k) then
do j=k,n
w=a(k, j)
a(k, j) = a(i_max,j)
a(i_max,j) = w
end do
end if
if (abs(a(k,k)).lt.eps) then
iflag = 0
return
end if
! ピボット選択終わり
do i=k+1, n
t=a(i,k)/a(k,k)
do j=k+1, n+1
a(i,j)=a(i,j)-t*a(k,j)
end do
end do
end do
if (abs(a(n,n)).lt.eps) iflag = 0
! 後退代入
do i=n,1, -1
d = a(i,n+1)
do j= n, i+1, -1
d=d- a(i,j)*a(j,n+1)
end do
a(i,n+1)=d/a(i,i)
end do
end
上のプログラムでは
とし、この連立方程式の解(の1つ)を求めている。
計算開始の初期値(x⁰,y⁰,z⁰)=(1,1,1)として計算した結果は次の通り。
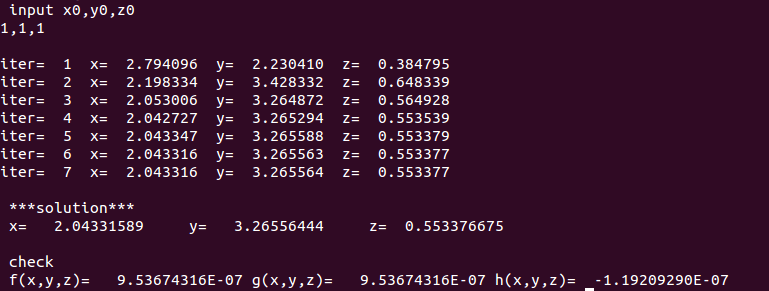




コメント 0